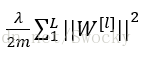数理统计专题
概率论与数理统计(1)
第一节博客已经整理了求导的公式,一些常用的概念。链接如下:高等数学基础(1)-CSDN博客。 第二节博客整理了微积分的公式及其相关概念。链接如下:高等数学基础(2)——微积分-CSDN博客 第三节博客则整理了泰勒公式和拉格朗日公式的相关概念。链接如下:高等数学基础(3)——泰勒公式与拉格朗日-CSDN博客 第四节博客则整理了行
【概率论与数理统计】第六章:数理统计基础
文章目录 一. 随机样本1. 总体与个体2. 总体对应随机变量X 二. 直方图和箱线图(ing)1. 直方图2. 箱线图 三. 抽样分布1. 统计量2. 三大样本分布2.1. 卡方分布2.2. t分布2.3. F分布 3. 正态总体的样本均值与样本方差的分布 数理统计(Mathematics Statistics)以概率论为基础,根据试验或者观察得到的数据来研究随机现象,对随机
概率论与数理统计期末复习
概率论常考知识点汇总 总括 1. 基础概率论 概率定义:理解概率是事件发生的可能性度量,范围从0(不可能)到1(必然发生)。概率公理:掌握概率的三大公理,即非负性、规范性和可加性。条件概率:P(A|B)表示在事件B已发生的条件下,事件A发生的概率。贝叶斯定理:用于计算在已知某些证据或数据的条件下,某个假设为真的概率。独立事件与相关事件:理解独立事件的概率乘法规则及相关事件的处理方
概率论与数理统计 -- 大数定理及切比雪夫不等式整理
大数定理、切比雪夫不等式及其推导 大数定律 弱大数定律(Weak Law of Large Numbers, WLLN) 弱大数定律指出,当试验次数 (n) 趋向无穷大时,样本平均值 (\bar{X_n}) 与期望值 (\mu) 之间的差异以概率收敛于0。数学上表示为: ∀ ϵ > 0 , lim n → ∞ P ( ∣ 1 n ∑ i = 1 n X i − μ ∣ ≥ ϵ ) =
漫步数理统计六——条件概率与独立(下)
$$\textbf{例5:}$瓶$C_1$中有$3$个红球,$7$个白球,瓶$C_2$中有$8$个红球,$2$个白球,这些球大小与形状都是一样的,现在假设选择瓶$C_1$的概率为$P(C_1)=\frac{2}{6}$,而选$C_2$的概率为$P(C_2)=\frac{4}{6}$。选完瓶子后我们随机抽一个球,抽到红球的事件用$C$表示,显然条件概率$P(C|C_1)=\frac{3}{10},P
漫步数理统计三——概率集合函数(上)
令 C \textbf{C}表示样本空间,那么事件集应该是什么呢?我们感兴趣的是给事件、事件的补、事件的并或交分配概率,因此我们希望事件集包含这些事件的组合,这样的事件集称为 C \textbf{C}子集的 σ \sigma域,定义如下: 定义1: \textbf{定义1:}( σ \sigma域)令 B \textbf{B}表示 C \textbf{C}子集的集合,如果 ϕ∈B \phi
漫步数理统计三十一——依分布收敛
上篇博文我们介绍了依概率收敛的概念,利用着概念我们可以说统计量收敛到一个参数,而且在许多情况下即便不知道统计量的分布函数也能说明收敛。但是统计量有多接近估计量呢?本篇博文讲的收敛就回答了这个问题。 定义1: \textbf{定义1:}(依分布收敛) {Xn} \{X_n\}是一系列随机变量, X X是随机变量。FXn,FXF_{X_n},F_X分别是 Xn,X X_n,X的cdf,令 C(Fx
漫步数理统计三十——依概率收敛
本篇博文我们将正式地陈述一系列随机变量靠近某个随机变量。 定义1: \textbf{定义1:} {Xn} \{X_n\}是一系列随机变量, X X是定义在样本空间上的随机变量。我们说XnX_n依概率收敛到 X X,如果对于ϵ>0\epsilon>0 limn→∞P[|Xn−X|≥ϵ]=0 \lim_{n\to\infty}P[|X_n-X|\geq\epsilon]=0
数据挖掘中所需的概率论与数理统计知识(补充)
1.极大似然估计原理详解: 2.共轭先验: 先验概率通常是主观的猜测,为了使计算后验概率方便,有时候会选择共轭先验。如果后验概率和先验概率是同一族的,则认为它们是共轭分布,这个先验概率就是对应于似然函数的共轭先验。 贝叶斯学派和频率学派的区别之一是特别重视先验信息对于inference的影响,而引入先验信息的手段有“贝叶斯原则“(即把先验信息当着均匀分布)等四大类 其
数理统计中95%置信区间的含义
95%置信区间,意味着如果你用同样的步骤,去选样本,计算置信区间,那么100次这样的独立过程,有95%的概率你计算出来的区间会包含真实参数值,即大概会有95个置信区间会包含真值。而对于某一次计算得到的某一个置信区间,其包含真值的概率,我们无法讨论。参源 1.点估计与区间估计 首先我们看看点估计的含义: 是用样本统计量来估计总体参数,因为样本统计量为数轴上某一点值,估计的结果也以一个点的数值表
数理统计复习笔记八——Kolmogorov检验
1. Kolmogorov检验 数理统计复习笔记六——Pearson卡方拟合优度检验说明了 χ 2 \chi^2 χ2拟合优度检验,如果分点选的不是很好,可能会把两个有一定差别的分布检验为没有区别,而Kolmogorov检验则可避免其不足。 由于样本经验分布函数 F n ( x ) F_n(x) Fn(x)(详见样本经验分布函数)是 F ( x ) F(x) F(x)的一个很好的估计,故当
数理统计复习笔记七——列联表的独立性检验
1. 一般的二维列联表 B 1 B_1 B1 B 2 B_2 B2 ⋯ \cdots ⋯ B s B_s Bs合计 A 1 A_1 A1 n 11 n_{11} n11 n 12 n_{12} n12 ⋯ \cdots ⋯ n 1 s n_{1s} n1s n 1 ⋅ n_{1\cdot} n1⋅ A 2 A_2 A2 n 21 n_{21} n21 n 22 n_{22}
数理统计复习笔记五——假设检验之显著性检验
一、基本概念 在统计中,我们把需要用样本去推断“正确”与否的命题称为一个假设。当然,假设是可以关于参数的,也可以是关于分布的。 通过样本对一个假设作出“对”或“不对”的具体判断规则就称为该假设的一个检验。检验的结果若“是”,则否定该命题,就称拒绝该假设,否则就称为接受原假设。这里的拒绝和接受原假设,只是在当前样本下作出的判断,并没有从逻辑或理论上“证明”该命题正确与否。 设有样本 X X X
[DataAnalysis]数据分析基础-茆诗松数理统计
一、充分统计量 总体分布函数为,统计量T称为θ的充分统计量,如果给定T的取值后,的条件分布与θ无关。 二、点估计 1、概念:是来自总体的一个样本,用于估计未知参数θ的统计量称为θ的估计量,或者称为θ的点估计。 2、评价标准:无偏性;有效性;相合性 三、EM算法:极大似然估计MLE是一种有效的参数估计方法,但是当分布中有多余参数或数据为截尾或缺失时,MLE的求取是比较困难的,于是引入EM算
概率论与数理统计 “保命” 复习冲冲冲
小田儿真快乐呀真快乐(bushi),持续更新中~ 文章目录 一、全概率与贝叶斯公式二、事件的独立性三、离散型随机变量分布律与分布函数四、连续型随机变量概率密度与分布函数五、离散型随机变量函数的分布六、连续型随机变量函数的分布七、二维离散型随机变量的分布八、二维连续型随机变量的分布九、二维离散型随机变量函数的分布十、二维连续型随机变量函数的分布十一、期望和方差十二、协方差和相关系数十三
概率论和数理统计知识点汇总
高等数学 高等数学 高等数学函数、极限、连续一元函数微分学一元函数积分学向量代数和空间解析几何多元函数微分学多元函数积分学无穷级数常微分方程 线性代数行列式向量线性方程组矩阵的特征值和特征向量 概率统计随机事件和概率变量的分布 随机变量函数的分布多维随机变量及其分布随机变量的数字特征大数定律和中心极限定理数理统计的基本概念参数估计假设检验 函数、极限、连续 考试要求 1.理解
概率论与数理统计 第一章 概率论的基本概念
文章目录 第一章 概率论的基本概念1.1 随机试验1.1.1 前言1.1.2 随机试验 1.2 样本空间、随机事件1.2.1 样本空间1.2.2 随机事件1.2.3 事件的关系、事件的运算、运算法则1.2.3.1 事件的关系1.2.3.2 事件的运算1.2.3.3 运算法则 1.3 频率与概率1.3.1 概率的描述性定义1.3.2 概率的统计性定义——频率1.3.3 概率的公理性定义 1.
5. 数理统计---极大似然估计
这里写自定义目录标题 5.极大似然估计5.1 似然函数定义5.2 极大似然估计定义5.3 极大似然估计求解的一般过程5.4 极大似然估计的不变性 5.极大似然估计 Fisher的极大似然思想: 随机试验有多个可能结果, 但在一次实验中, 有且只有一个结果会出现. 如果在某次实验中, 结果 ω \omega ω出现了, 则认为该结果(事件{ ω \omega ω})发生的概率 P
2. 数理统计---样本分布
2. 样本分布 定义1: 统计量 g ( X 1 , X 2 , . . . , X n ) g(X_1, X_2, ..., X_n) g(X1,X2,...,Xn)的分布称为抽样分布. 主要介绍与标准正态总体相关的抽样分布. 包括, χ 2 \chi^2 χ2分布, t t t分布和 F F F分布. 2.1 χ 2 \chi^2 χ2分布 定义2: 设 X 1 , X 2
【数理统计实验(四)】方差分析
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一|统计学|干货分享 擅长Python、Matlab、R等主流编程软件 累计十余项国家级比赛奖项,参与研究经费10w、40w级横向 文章目录 1 题目背景2. 方差分析3 多重比较4 正态性检验5 方差齐性检验 该篇文
概率论与数理统计 P6 条件概率
文章目录 P6 条件概率一.条件概率二.乘法定理三.全概率公式 & 贝叶斯公式3.1 全概率公式(由因求果)3.2 贝叶斯公式(由果导因) P6 条件概率 一.条件概率 1.Def:设A、B是两个事件,且 P ( A ) > 0 P(A)>0 P(A)>0,称 P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\dfrac{P(AB)}{P(A
[渝粤教育] 中国地质大学 概率论与数理统计 复习题 (2)
《概率论与数理统计》模拟题 一.单选题 1.对于事件AB下列命题正确的是(). A.若AB互不相容则与也互不相容. B.若AB相容那么与也相容. C.若AB互不相容且概率都大于零则AB也相互独立. D.若AB相互独立那么与也相互独立. 2.在一次假设检验中下列说法正确的是(). A.既可能犯第一类错误也可能犯第二类错误 B.如果备择假设是正确的但作出的决策是拒绝备择假设则犯了第一类错误 C.增
DPSS quant 1.1 因果 芝加哥大学Uchicago暑校数理统计部分
Causality 1.1 因果(Causality)1.1.1 Motivation1.1.1.1 例子1.1.1.2 例子 1.1.2 Rubin Model1.1.2.1 Estimator1.1.2.2 Assignment MachanismRubin‘s “Perfect Doctor” 1.1.3 Non-Causal Relationships1.1.4 Conclusio
【个人总结】概率论与数理统计在人工智能领域的应用
概率论与数理统计在人工智能领域的应用 概率论与数理统计在人工智能领域的应用一、绪论1.新人工智能时代2.基础数学理论的作用3.概率论与数理统计应用概述 二、深度学习原理三、概率论与深度学习1.深度学习中的随机事件2.基于概率的预测分析3.概率分布的应用 四、统计学与深度学习1.拟合2.偏差与方差3.正则化5.归一化 五、小结六、参考文献 概率论与数理统计在人工智能领域的应用 由
数理统计之协方差矩阵
文章目录 前言:1.方差2.协方差3.协方差矩阵4.相关系数矩阵协方差矩阵与PCA的联系 前言: 本文介绍数理统计和机器学习中的一个非常重要的概念:协方差矩阵(即随机变量的数字特征)。理解好这个概念将有助于对机器学习的相关内容如:主成分分析(即PCA:Principal Component Analysis),线性判别分析(即LDA:Linear Discriminant A






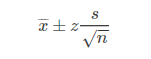
![[DataAnalysis]数据分析基础-茆诗松数理统计](https://img-blog.csdn.net/2018081117435367?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1RPTU9DQVQ=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)