概率论与数理统计 “保命” 复习冲冲冲

2024-04-07 16:38

文章标签 复习概率论冲冲数理统计保命

本文主要是介绍概率论与数理统计 “保命” 复习冲冲冲，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

小田儿真快乐呀真快乐（bushi），持续更新中~

文章目录

- 一、全概率与贝叶斯公式
- 二、事件的独立性
- 三、离散型随机变量分布律与分布函数
- 四、连续型随机变量概率密度与分布函数
- 五、离散型随机变量函数的分布
- 六、连续型随机变量函数的分布
- 七、二维离散型随机变量的分布
- 八、二维连续型随机变量的分布
- 九、二维离散型随机变量函数的分布
- 十、二维连续型随机变量函数的分布
- 十一、期望和方差
- 十二、协方差和相关系数
- 十三、中心极限定理
- 十四、三大分布
- 十五、点估计
- 十六、假设检验

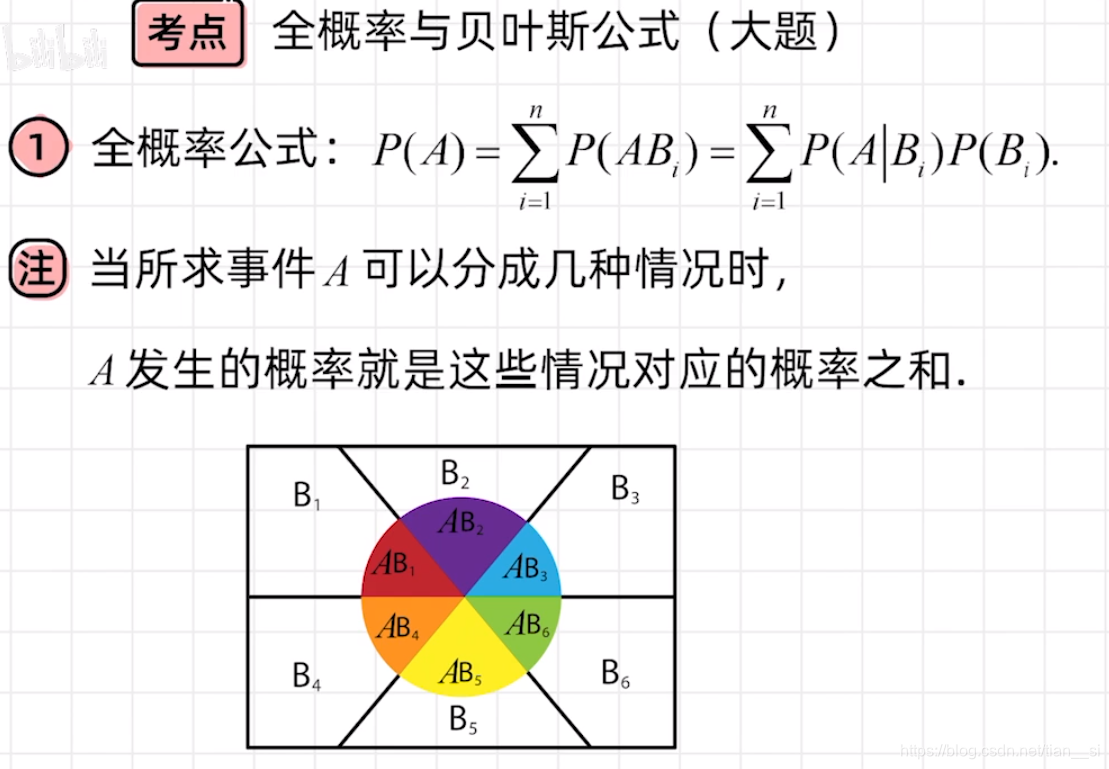
一、全概率与贝叶斯公式

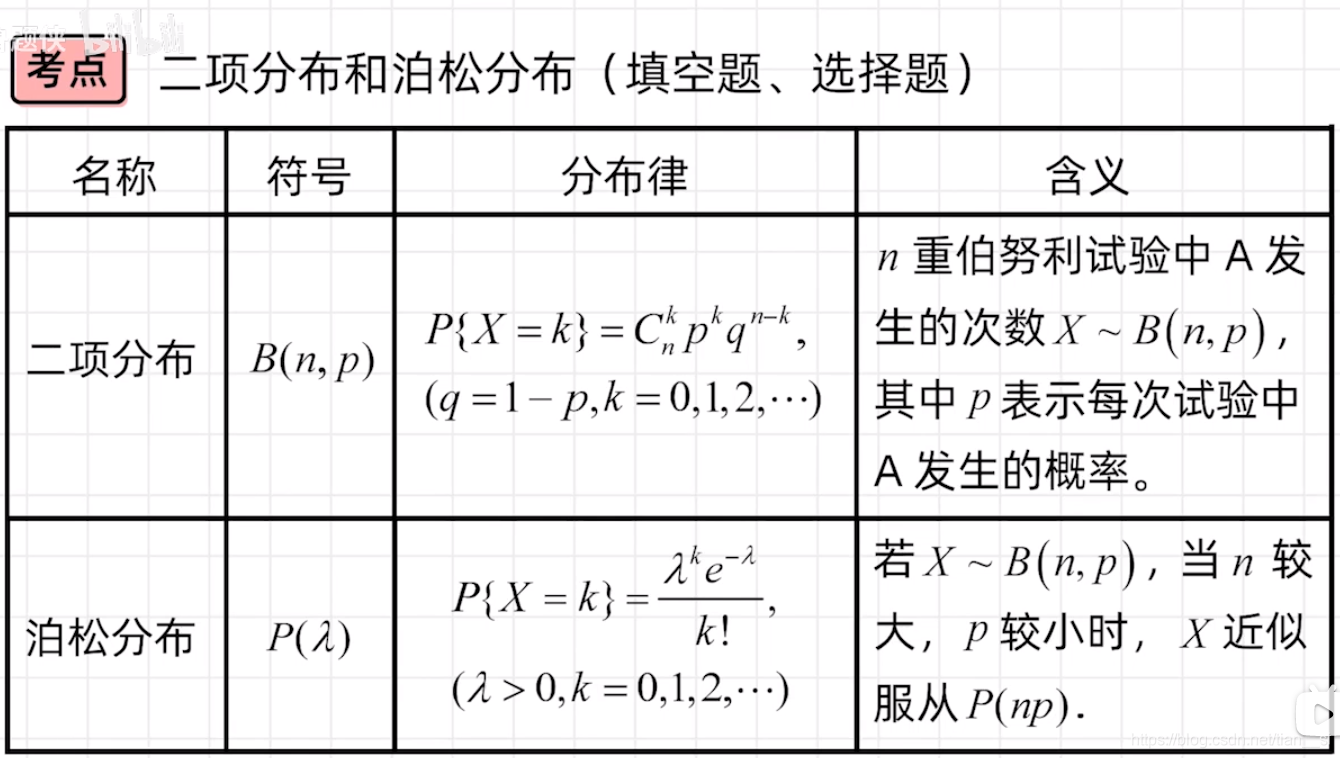
在这里插入图片描述

在这里插入图片描述

二、事件的独立性

在这里插入图片描述

三、离散型随机变量分布律与分布函数

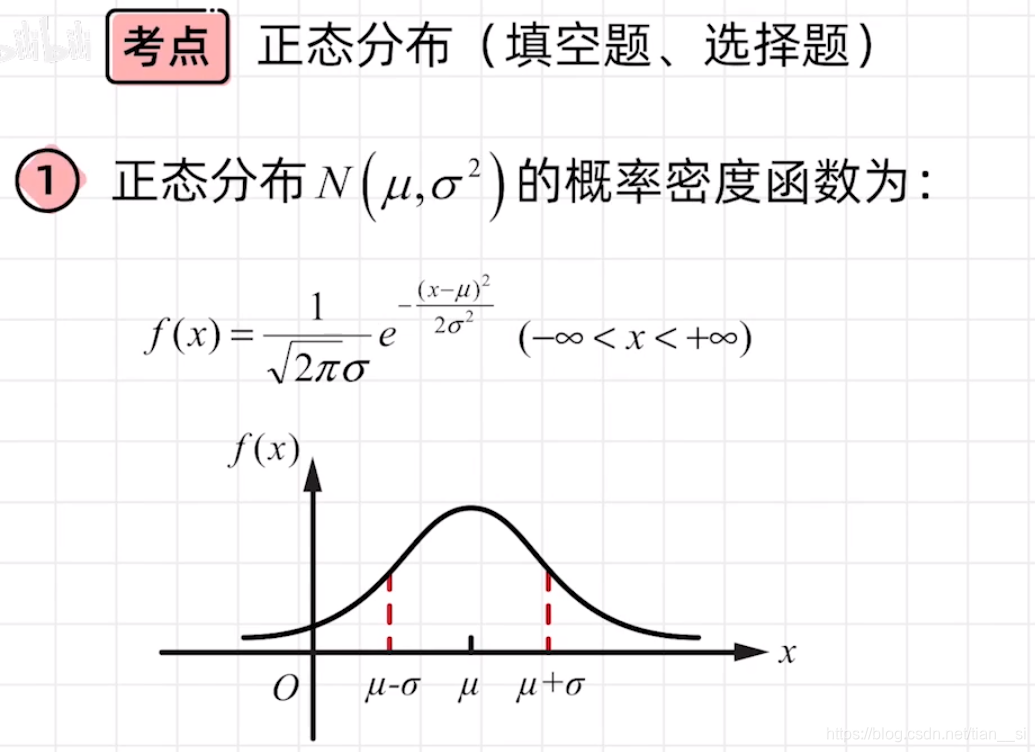
在这里插入图片描述

四、连续型随机变量概率密度与分布函数

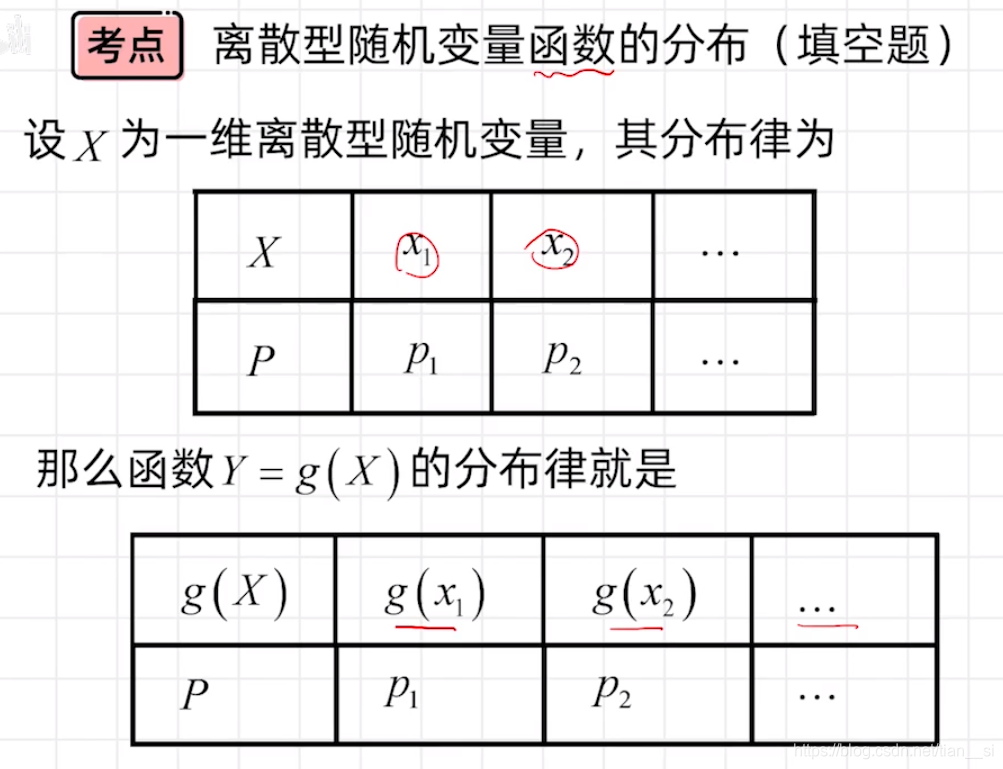
在这里插入图片描述

五、离散型随机变量函数的分布

在这里插入图片描述

六、连续型随机变量函数的分布

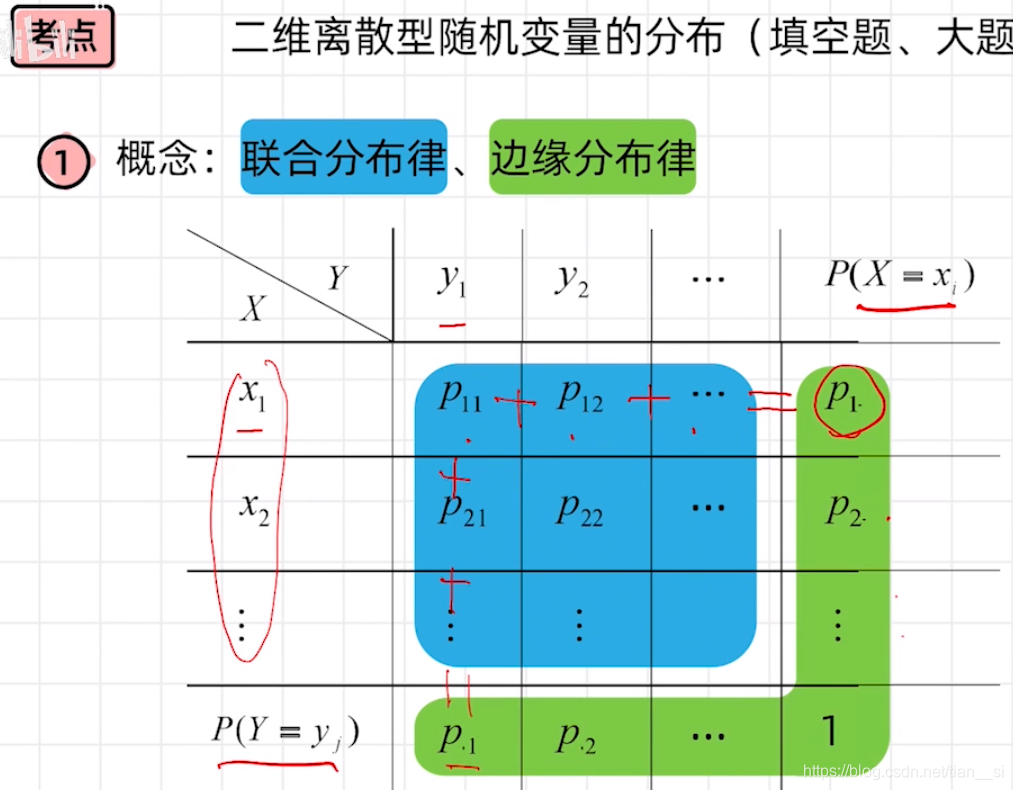
在这里插入图片描述

七、二维离散型随机变量的分布

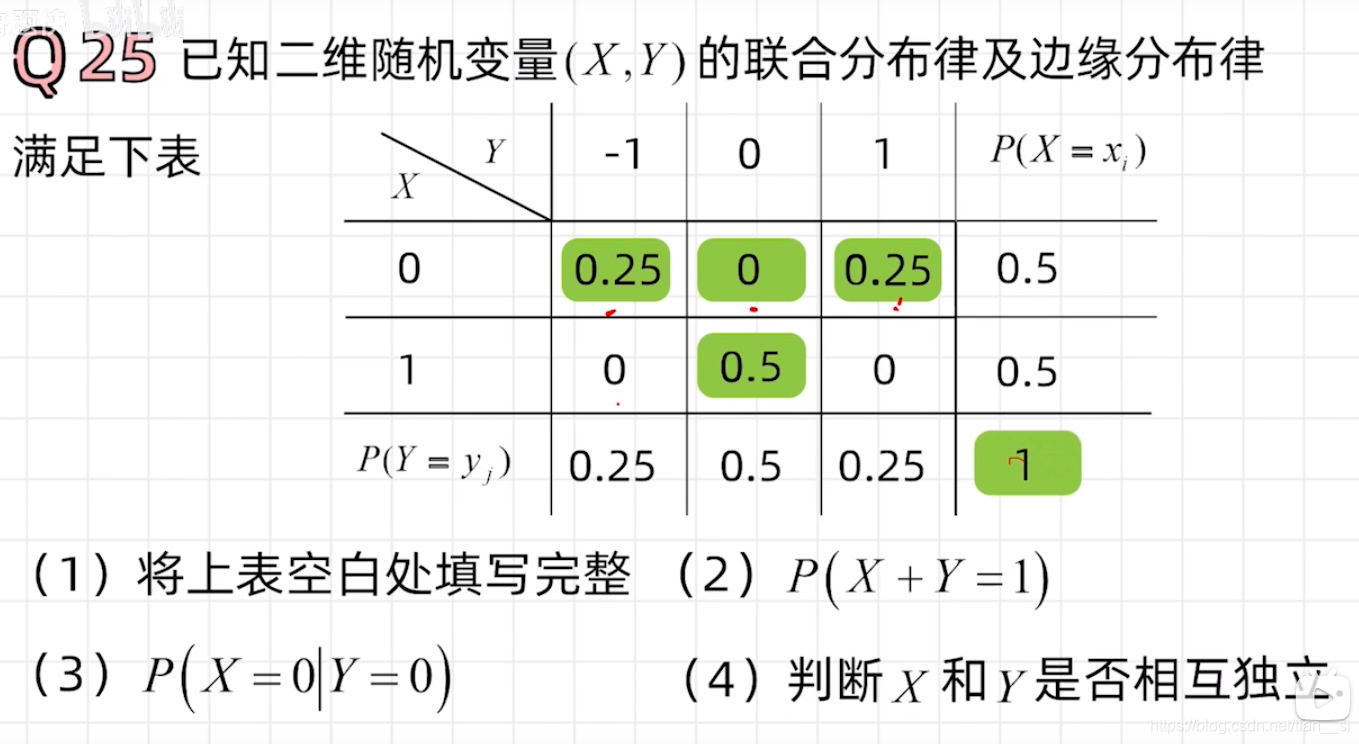
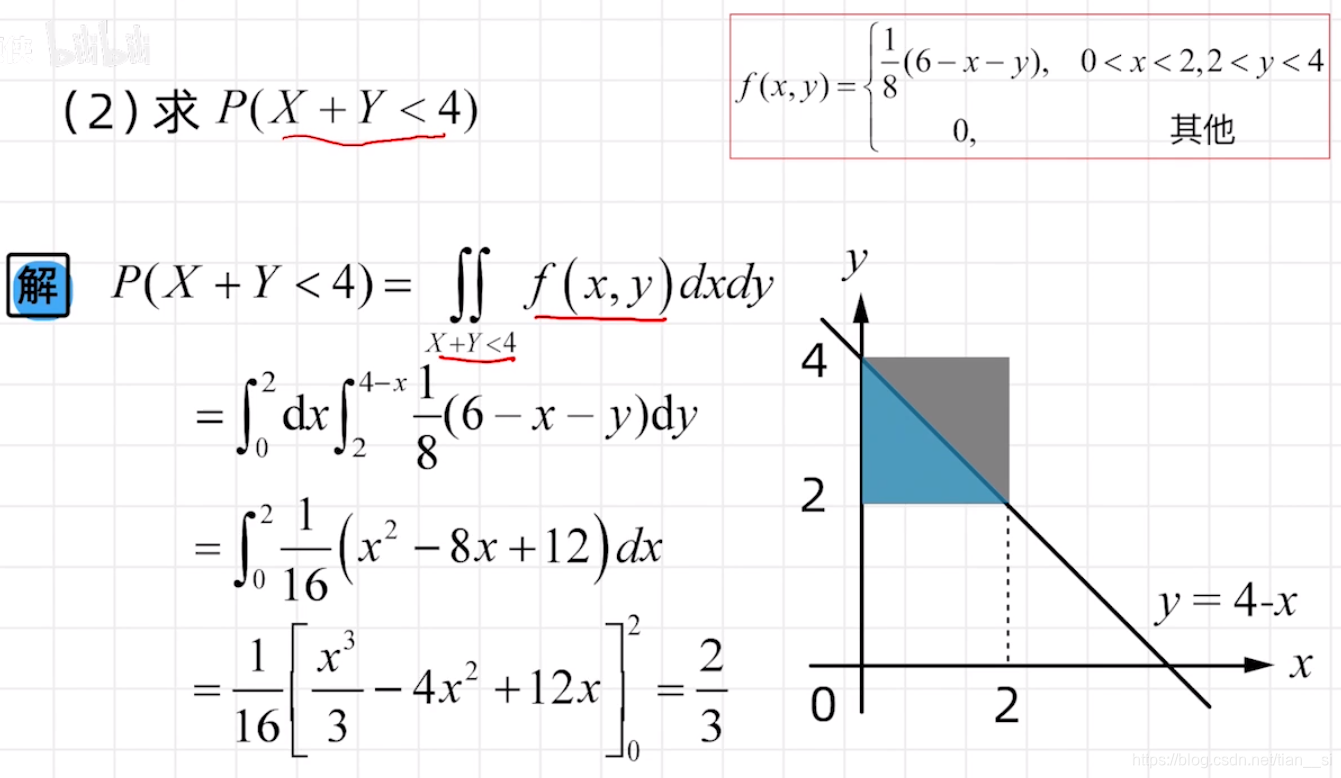
在这里插入图片描述

八、二维连续型随机变量的分布

在这里插入图片描述

九、二维离散型随机变量函数的分布

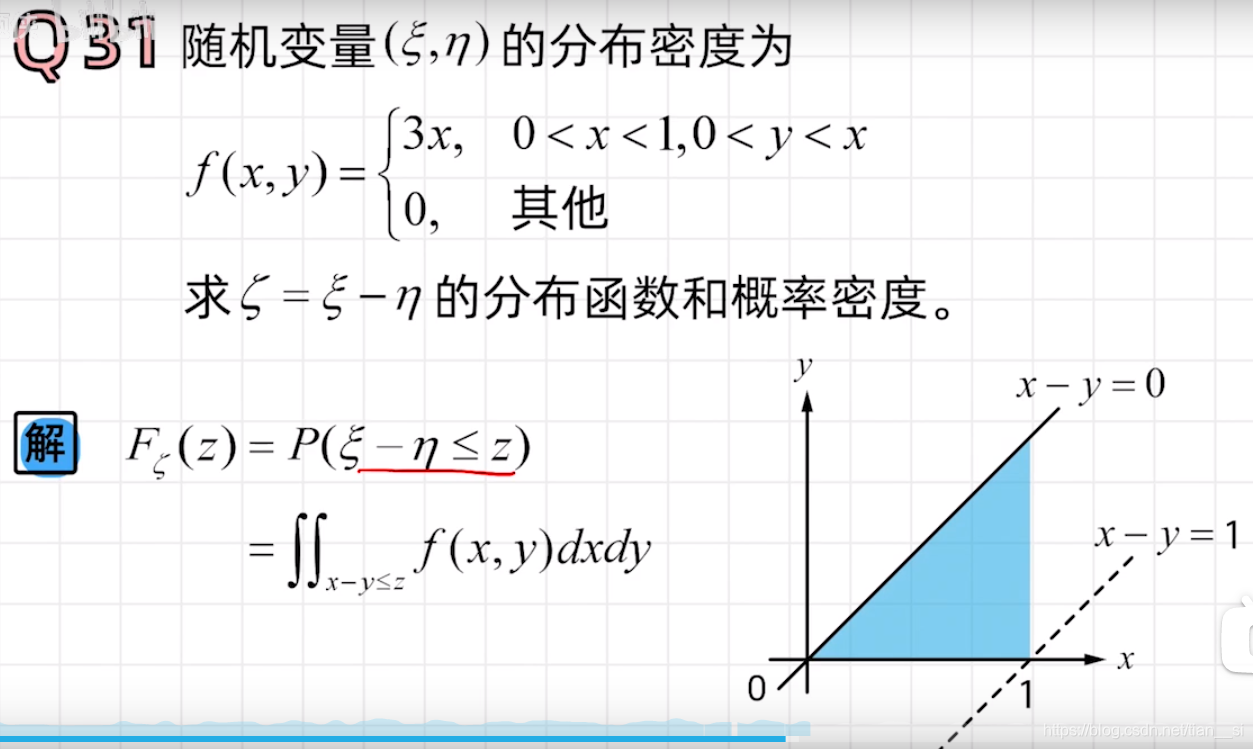
在这里插入图片描述

十、二维连续型随机变量函数的分布

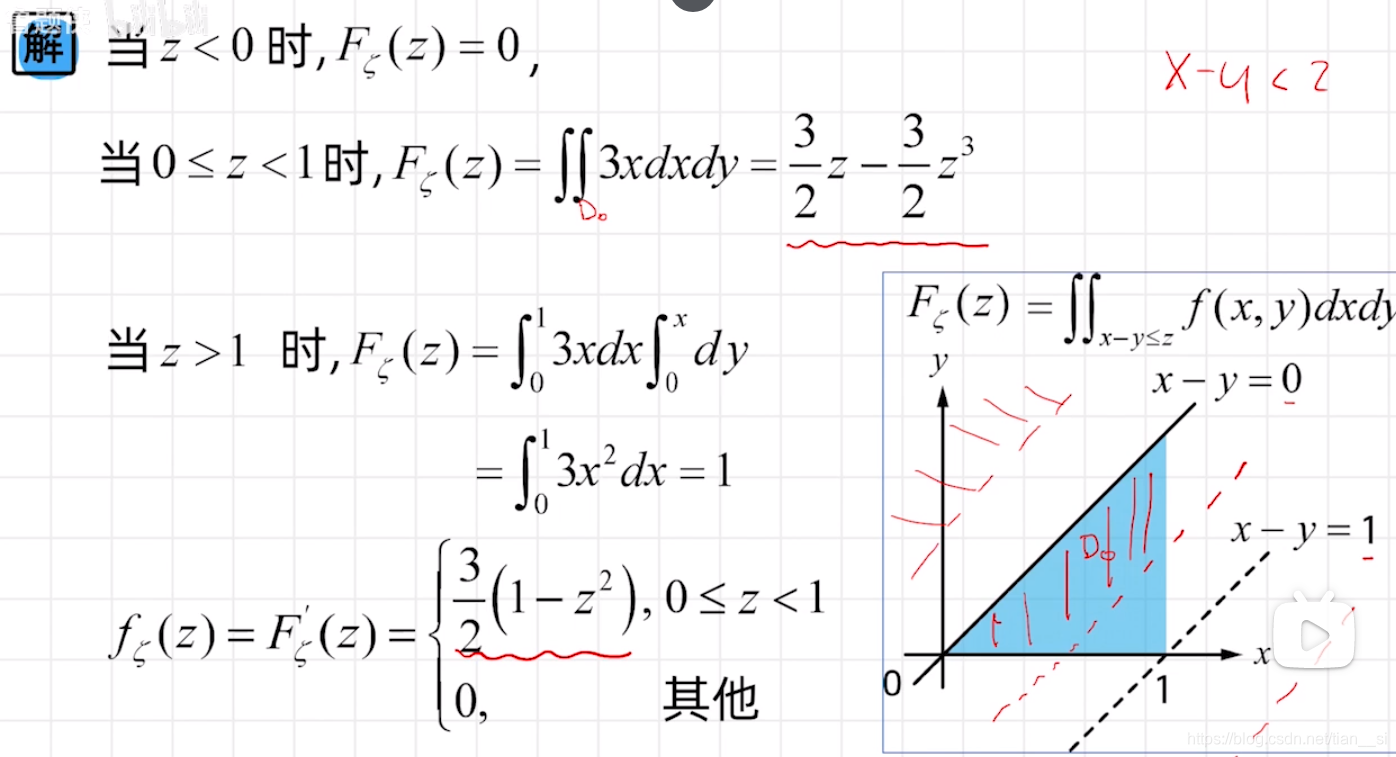
在这里插入图片描述

在这里插入图片描述

十一、期望和方差

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

十二、协方差和相关系数

在这里插入图片描述

在这里插入图片描述

十三、中心极限定理

中心极限定理就是用正态分布近似一般的分布

在这里插入图片描述

在这里插入图片描述

十四、三大分布

在这里插入图片描述

十五、点估计

点估计 = 矩估计 + 极大似然估计

在这里插入图片描述

极大似然估计：已经出现的，就是最有可能出现的

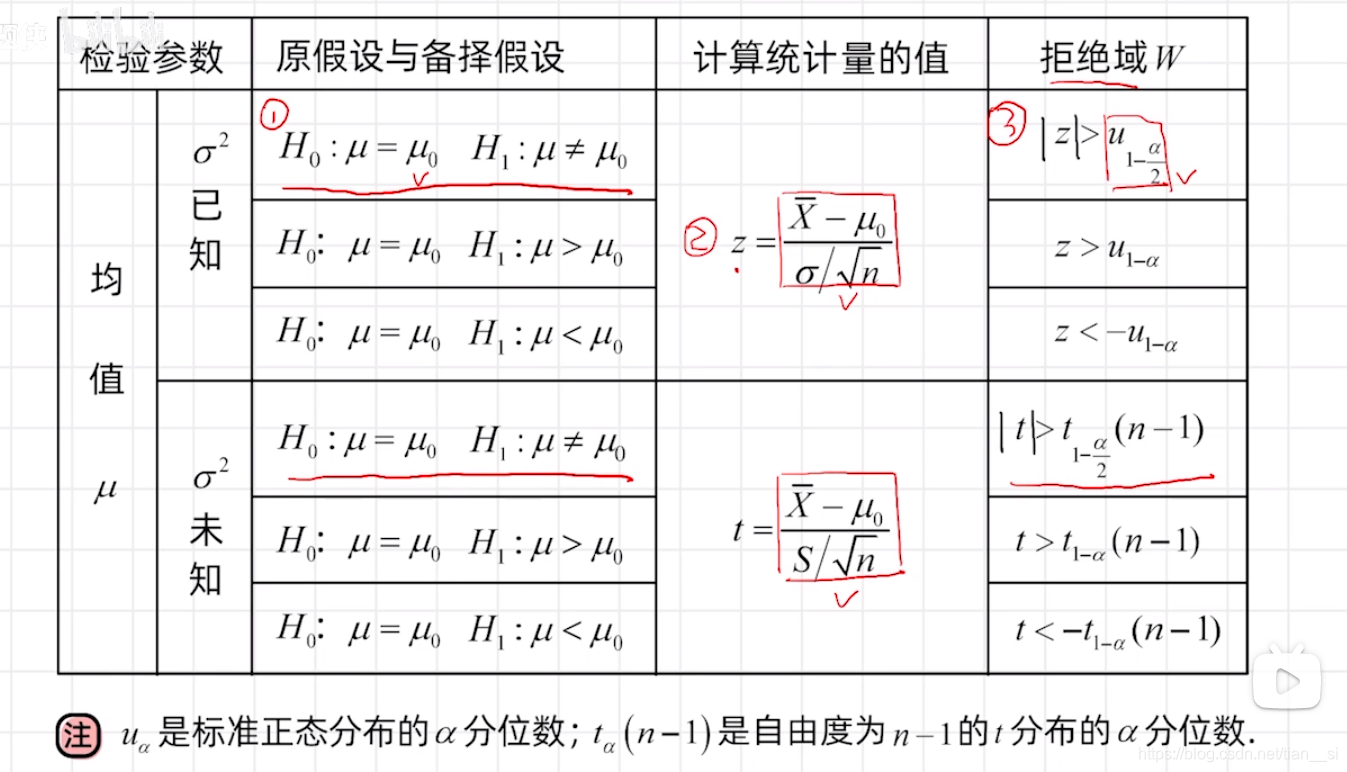
在这里插入图片描述

十六、假设检验

假设检验的本质是检验一个条件是否成立

在这里插入图片描述

这篇关于概率论与数理统计 “保命” 复习冲冲冲的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/883114。 23002807@qq.com

相关文章

代码随想录冲冲冲 Day39 动态规划Part7

代码随想录冲冲冲 Day39 动态规划Part7

198. 打家劫舍 dp数组的意义是在第i位的时候偷的最大钱数是多少如果nums的size为0 总价值当然就是0 如果nums的size为1 总价值是nums[0] 遍历顺序就是从小到大遍历之后是递推公式对于dp[i]的最大价值来说有两种可能 1.偷第i个那么最大价值就是dp[i-2]+nums[i] 2.不偷第i个那么价值就是dp[i-1] 之后取这两个的最大值就是d

阅读更多...

【408数据结构】散列（哈希）知识点集合复习考点题目

【408数据结构】散列（哈希）知识点集合复习考点题目

苏泽 “弃工从研”的路上很孤独，于是我记下了些许笔记相伴，希望能够帮助到大家知识点 1. 散列查找散列查找是一种高效的查找方法，它通过散列函数将关键字映射到数组的一个位置，从而实现快速查找。这种方法的时间复杂度平均为(

阅读更多...

机械学习—零基础学习日志（概率论总笔记5）

机械学习—零基础学习日志（概率论总笔记5）

引言——“黑天鹅” 要获得95%以上置信度的统计结果，需要被统计的对象出现上千次，但是如果整个样本只有几千字，被统计的对象能出现几次就不错了。这样得到的数据可能和真实的概率相差很远。怎么避免“黑天鹅”？古德-图灵折扣估计法在词语统计中，有点词语虽然是出现0次，但是实际的出现概率并不是永远不可能的零。那需要把一些概率转移给到这些词语。古德的做法实际上就是把出现1次的单词的总量，给了

阅读更多...

计算机基础知识复习9.6

计算机基础知识复习9.6

点对点链路：两个相邻节点通过一个链路相连，没有第三者应用：PPP协议，常用于广域网广播式链路：所有主机共享通信介质应用：早期的总线以太网，无线局域网，常用于局域网典型拓扑结构：总线型星型（逻辑总线型）介质访问控制静态划分信道信道划分介质访问控制频分多路复用FDM 时分多路复用TDM 波分多路复用WDM 码分多路复用CDM 动态分配信道轮询访问介质访问控

阅读更多...

【抽代复习笔记】28-群（二十二）：四道子群例题

【抽代复习笔记】28-群（二十二）：四道子群例题

例1：证明，循环群的子群是循环群。证：设G = (a)，H ≤ G。（1）若H = {e}，则H是一阶循环群；（2）设H至少包含2个元素，即设H = {...,a^(-k),a^(-j),a^(-i),a^0,a^i,a^j,a^k,...}，其中a^i是H中正指数最小的元素，0＜i＜j＜k，下证a^i是H的生成元：对任意的a^t∈H(t∈Z)，存在q∈Z，使得t = qi

阅读更多...

西方社会学理论教程复习重点

西方社会学理论教程复习重点

一．名词解释 1.社会静力学：旨在揭示人类社会的基本秩序。它从社会的横断面，静态的考察人类社会的结构和制度，寻找确立和维护人类社会的共存和秩序的原则。 2.社会动力学：纵观人类理性和人类社会发展的先后必要阶段，所叙述的是这一基本秩序在达到实证主义这一最终阶段之前所经过的曲折历程。 3.社会事实：一切行为方式，不论它是固定的还是不固定的，凡是能从外部给予个人以约束的，或者说是普遍存在于该社会各

阅读更多...

完整版自考西方文论选复习笔记资料

完整版自考西方文论选复习笔记资料

西方文论选读复习资料 1．柏拉图：古希腊哲学家，苏格拉底的学生。公园前387年在雅典城外建立学园开始授徒讲学，撰写对话。柏拉图的作品即《柏拉图文艺对话集》中讨论美学和文艺理论问题较多的有：《大希庇阿斯》、《伊安》、《高吉阿斯》、《会饮》、《斐德若》、《理想国》、《斐利布斯》、《法律》等。 ▲柏拉图《伊安》和《斐若德》内容：主要阐述了"迷狂说"和"灵魂回忆说"：柏拉图认为，高明的诗人都是凭灵

阅读更多...

ia复习笔记

ia复习笔记

HCIA 常用配置以及快捷键：! 查看时间：display clock；修改时间：clock datetime 11:11:11 2023-1-1 查看设备当前的配置：display current-configuration；查看已保存的配置：display saved-configuration；保存配置：save；查看历史的十条命令：display history-command；

阅读更多...

android kotlin复习 Anonymous function 匿名函数

android kotlin复习 Anonymous function 匿名函数

1、还是先上个图，新建kt： 2、代码： package com.jstonesoft.myapplication.testfun main(){val count = "helloworld".count()println(count);println("------------------------")var count2 = "helloworld".count(){it ==

阅读更多...

C++复习day05

C++复习day05

类和对象 1. 面向对象和面向过程的区别是什么？（开放性问题） 1. **抽象级别**：- **面向对象**：以对象（数据和方法的集合）为中心，强调的是数据和行为的封装。- **面向过程**：以过程（函数或子程序）为中心，强调的是步骤和顺序。2. **数据和方法的关系**：- **面向对象**：数据和处理数据的方法封装在对象中，对象可以包含数据和操作数据的方法。- **面向过程**：数据和处理

阅读更多...