【数理统计实验（四）】方差分析

本文主要是介绍【数理统计实验（四）】方差分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972

个人介绍: 研一｜统计学｜干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项，参与研究经费10w、40w级横向

文章目录

1 题目背景
2. 方差分析
3 多重比较
4 正态性检验
5 方差齐性检验

该篇文章以实际例子形式，利用R语言完成方差分析相关代码及结果分析，其中包括样本的方差分析；多重比较；正态性检验；方差齐性检验。

1 题目背景

用4种安眠药在兔子身上进行试验，特选24只健康的兔子，随机把他们均分为4组，各组各服一种安眠药，安眠时间（单位：h）如下所示.

安眠药试验数据：

在显著性水平α=0.05下对其进行方差分析，可以得到什么结果？

2. 方差分析

运行程序：

X <- c(6.2,6.1,6.0,6.3,6.1,5.9,6.3,6.5,6.7,6.6,7.1,6.4,
6.8,7.1,6.6,6.8,6.9,6.6,5.4,6.4,6.2,6.3,6.0,5.9)#将不同水平下测试的样本值放入一个向量内
A<-factor(rep(1:4,each=6))#题目中有四个水平，每个水平有6个观测值
miscellany<-data.frame(X,A)#由数据X和水平A建立数据框
aov.mis<-aov(X~A,data=miscellany) #调用幻术aov()进行方差分析的计算与检验
summary(aov.mis)#显示结果

运行结果：

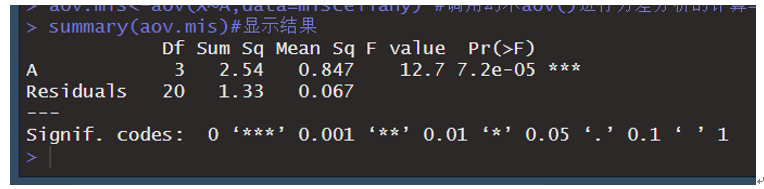
通过方差分析的结论可以看出，检验统计量F的自由度为3，总平方和等于2.54，均方和等于0.847，F检验统计量等于12.7，Pr(>F)表示P值=7.2e-05<0.05，故拒绝原假设，即认为四种安眠药对兔子的安眠时间有显著差异，即认为四种安眠药的效果有显著差异。

根据上述结果可以写出方差分析表：

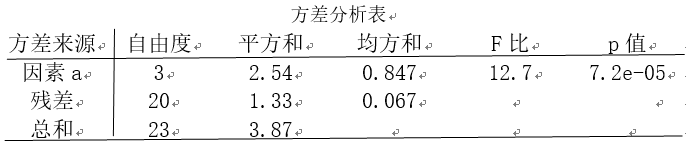
3 多重比较

通过对题目进行方差分析后，我们利用方差分析结果，使用TukeyHSD()函数进行多重比较，，即两两安眠药之间的效果比较。

运行程序：

TukeyHSD(aov.mis)#对方差分析结果进行多重比较，即两两安眠药之间的效果比较

运行结果：

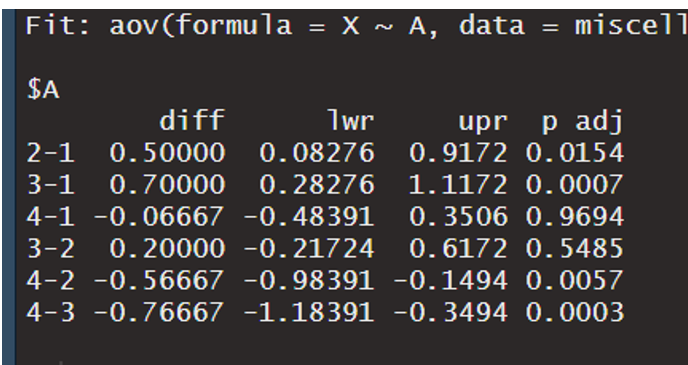
通过运行结果，我们可以看出两两水平之间的比较，共有6组，且结果显示了每个水平均值差的置信水平，和p值，根据p值可以看出1和4,2和3的差异不显著，其他两两之间的差异都显著。

4 正态性检验

使用Shapiro-Wilk检验进行正态性分析：

运行程序：

X <- c(6.2,6.1,6.0,6.3,6.1,5.9,6.3,6.5,6.7,6.6,7.1,6.4,
6.8,7.1,6.6,6.8,6.9,6.6,5.4,6.4,6.2,6.3,6.0,5.9)#将不同水平下测试的样本值放入一个向量内
shapiro.test(X)#进行正态性检验

运行结果：

通过运行结果，可以看出p值=0.8>0.05，即可以认为其近似服从正态分布。

5 方差齐性检验

此处使用Bartlett检验。

运行程序：

X <- c(6.2,6.1,6.0,6.3,6.1,5.9,6.3,6.5,6.7,6.6,7.1,6.4,
6.8,7.1,6.6,6.8,6.9,6.6,5.4,6.4,6.2,6.3,6.0,5.9)#将不同水平下测试的样本值放入一个向量内
A<-factor(rep(1:4,each=6))#题目中有四个水平，每个水平有6个观测值
miscellany<-data.frame(X,A)#由数据X和水平A建立数据框
bartlett.test(X~A,data=miscellany)#进行方差齐性检验

运行结果：