本文主要是介绍DPSS quant 1.1 因果 芝加哥大学Uchicago暑校数理统计部分,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Causality
- 1.1 因果(Causality)
- 1.1.1 Motivation
- 1.1.1.1 例子
- 1.1.1.2 例子
- 1.1.2 Rubin Model
- 1.1.2.1 Estimator
- 1.1.2.2 Assignment Machanism
- Rubin‘s “Perfect Doctor”
- 1.1.3 Non-Causal Relationships
- 1.1.4 Conclusion
1.1 因果(Causality)
1.1.1 Motivation
理清数据间的因果关系对于解释和指导现实世界具有重要意义
1.1.1.1 例子
1665年,伦敦爆发鼠疫,是时人们猜测鼠疫成因与动物有关,并因此屠杀了40000余狗和5倍于此的猫
当时的数据表明,猫的数量与黑死病死亡数正相关,烟雾与黑死病死亡数负相关
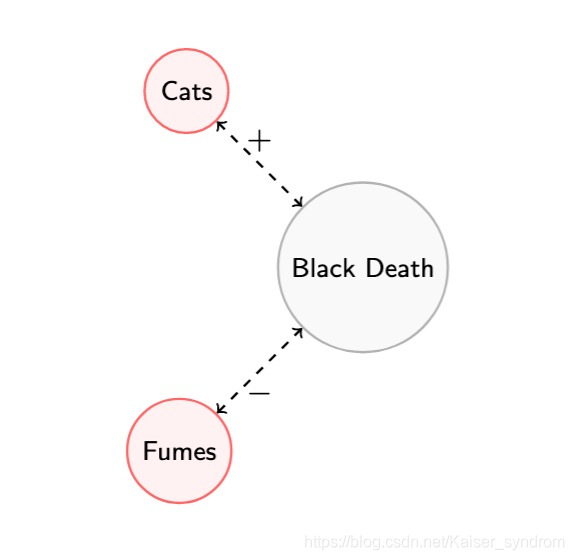
看起来,杀死猫似乎并非毫无根据,然而事实是这样的

有老鼠滋蔓的地方黑死病的死亡数更高,而因为有老鼠,这里的猫才会更多!杀死猫只会增加死亡数量!
1.1.1.2 例子
1854年,伦敦医生John Snow通过分析患者分布推测水源出现污染,成功避免了感染进一步扩大
1.1.2 Rubin Model
对于给定的对象i和一种干涉(intervention)t,对i有状态世界 S , S ∈ { t , c } S,S\in \{t,c\} S,S∈{t,c},其中t和c分别对应实验(施加干涉)和对照(不施加干涉),记其对应的结果(outcome by the measure of interest)为 Y Y Y,用下标i对应对象,用上标S表示是否施加干涉。
所谓的因果影响(Causal Effect)即是潜在的两种结果( Y i t , Y i c Y_i^t,Y_i^c Yit,Yic)的不同 Y i t − Y i c = T i Y_i^t-Y_i^c=T_i Yit−Yic=Ti,t对于c的TE(treatment effect)也是 Y i t − Y i c = T i Y_i^t-Y_i^c=T_i Yit−Yic=Ti
然而有一个很核心的问题(Fundmental problem of causal inference)——你只能看到潜在结果中的一个,不可能在现实世界同时观测到两种结果!(这就意味着任意一个对象的TE是不可知的)
1.1.2.1 Estimator
因为对于任意给定 i i i, T i T_i Ti都是不可知的,所以我们放弃计算每个特定的 T i T_i Ti(intervention在i上的TE),转而计算ATE(average treatment effect, 平均实验效果)
T = E ( Y i t − Y i c ) = E ( T i ) T=E(Y_i^t-Y_i^c)=E(T_i) T=E(Yit−Yic)=E(Ti)
(这个公式假设了 T i T_i Ti是对应研究对象的简单随机样本或者相应的随机变量)
T也是不可观测的,但是现实中我们可以估算
T ^ = E ^ ( Y i t ∣ S = t ) − E ^ ( Y i c ∣ S = c ) \hat T=\hat E(Y_i^t|S=t)-\hat E(Y_i^c|S=c) T^=E^(Yit∣S=t)−E^(Yic∣S=c)
$\hat T 是 否 是 一 个 是否是一个 是否是一个T$的好的估计取决于取样方式(assignment mechanism)
若满足下列条件,则可以认为 T ^ \hat T T^是一个好的估计
E ( Y i t ) = E ( Y i t ∣ S = t ) E ( Y i c ) = E ( Y i t ∣ S = c ) E(Y_i^t)=E(Y_i^t|S=t) \\ E(Y_i^c)=E(Y_i^t|S=c) E(Yit)=E(Yit∣S=t)E(Yic)=E(Yit∣S=c)
此时
E ( T ^ ) = T E(\hat T)=T E(T^)=T
当S与Y相互独立,上述条件就会被满足(注:完全随机的分配S看似合理,但是无法验证)
以上公式均来自ppt,容易发现公式在细节上并未深究,例如 E ( E ^ ( Y i t ∣ S = t ) ) E(\hat E(Y_i^t|S=t)) E(E^(Yit∣S=t))因某种未知的良好估计方式确定的等于 E ( Y i t ∣ S = t ) E(Y_i^t|S=t) E(Yit∣S=t); i i i被视为某个 o b j e c t object object,但 T i T_i Ti又被视为样本,这也在公式中造成了混淆
1.1.2.2 Assignment Machanism
Rubin‘s “Perfect Doctor”
现研究某种疾病的一个病人群体,对这种病有一种手术方法,对于某些人有利而对某些人有害,现有一个完美的医生他可以洞悉病人施加手术和不施加手术的两种未来,从而总是对需要手术的人手术,对不需要手术的人不手术
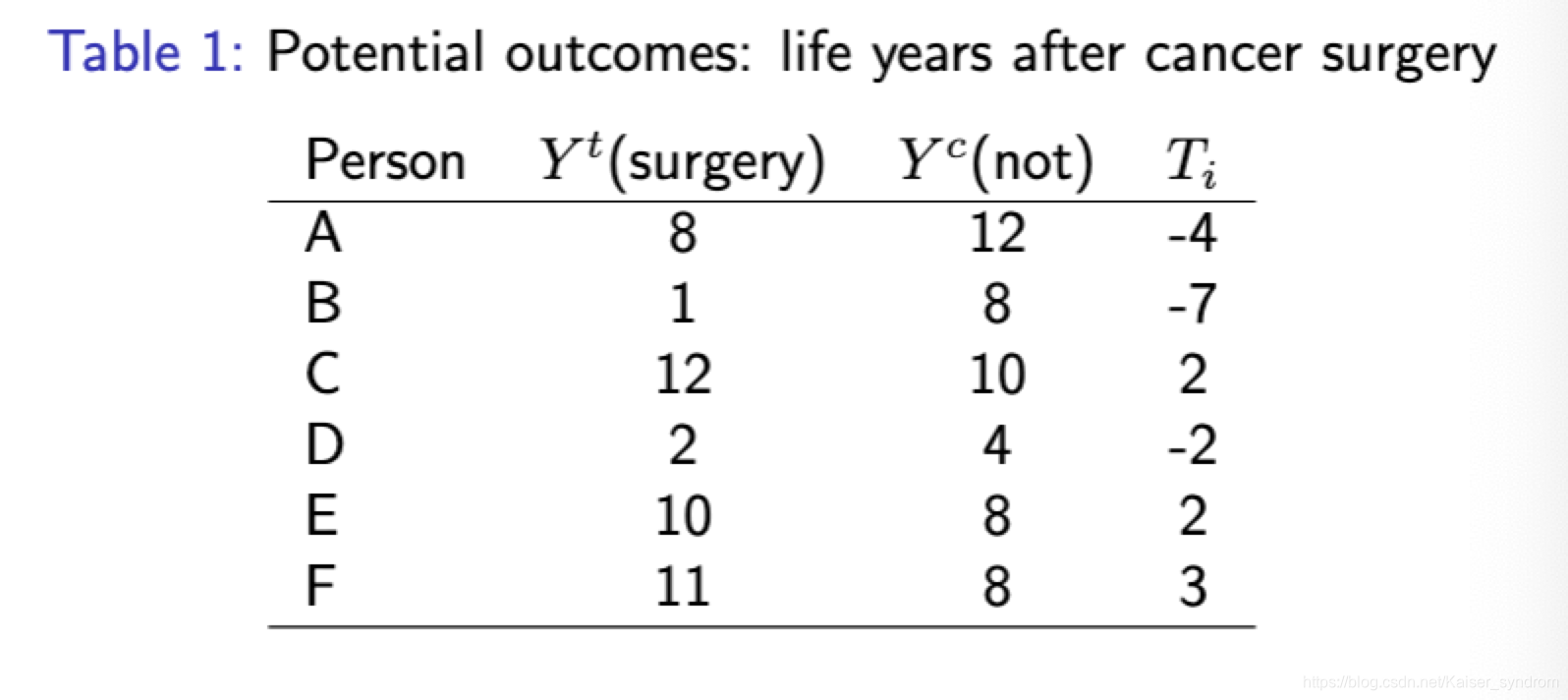
实验结束后我们得到如下结果

从第一张表我们发现,这种手术的平均效果是差的(术后平均减寿1年),但根据第二张表我们估算T,结果则是该手术对病人在平均意义上具有积极影响(术后平均延寿3年)
这个医生总是因地制宜,给特定病人施加最好的state
在现实生活中,对于实际的社会问题,我们往往会有知识(例如,救济前往往知道被救济者的收入和消费情况),这种知识辅助了我们更好的实行某种干涉,同时也使得我们在平均意义上的估计可能出现很大的偏差。
1.1.3 Non-Causal Relationships
非因果关系常常很重要,我们将在此后学习估计非因果关系的数理统计方法
一般来说,我们总是想要先搞清楚变量间的关系,然后我们再试图搞清表象背后的实质,那也许是因果
- 例如,在黑死病的例子中,我们首先发现猫与黑死病死亡数的正相关关系,然后找到了两者间的因果关系——即猫-鼠-蚤-鼠疫-死亡的影响链条
1.1.4 Conclusion
-
不是所有的数据关系都是因果关系(causal relationships)
-
即使存在因果关系,也需要合理的取样方法才能克服因果推断的基本问题(也就是不能同时观测到两个未来的问题)
-
要客观看待问题——人们经常试图强行解释数据,为数据强行施加因果关系,这常常都是不合理的!(例如,猫就被扣上了传播鼠疫的帽子,这就离谱)
这篇关于DPSS quant 1.1 因果 芝加哥大学Uchicago暑校数理统计部分的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!