本文主要是介绍【个人总结】概率论与数理统计在人工智能领域的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
概率论与数理统计在人工智能领域的应用
- 概率论与数理统计在人工智能领域的应用
- 一、绪论
- 1.新人工智能时代
- 2.基础数学理论的作用
- 3.概率论与数理统计应用概述
- 二、深度学习原理
- 三、概率论与深度学习
- 1.深度学习中的随机事件
- 2.基于概率的预测分析
- 3.概率分布的应用
- 四、统计学与深度学习
- 1.拟合
- 2.偏差与方差
- 3.正则化
- 5.归一化
- 五、小结
- 六、参考文献
概率论与数理统计在人工智能领域的应用
由于概率论课程作业要求,以及之前对于深度学习有了一点点了解,所以写了本文,一方面进行个人学习总结,另一方面与大家分享一些观点。初学人工智能、概率论及统计,本文不恰当之处还请大家包涵与指正。
一、绪论
1.新人工智能时代
尽管摩尔定律失效的趋势已不可避免,近十年内硬件性能已然取得了重大的突破。超级计算机、高性能个人电脑已经逐渐走进我们的生活。这样的契机下,过去因计算性能不足而搁置的诸多人工智能理论又焕发了新的生机。
无论是自然语言处理还是计算机视觉,大数据分析或是语音识别,人工智能的发展给我们带来的便利已经融入了我们生活的方方面面。计算机能够认识图片中的事物、能够听懂人类的指令、能够自主的聊天、能够玩电子游戏,甚至战胜世界第一的围棋选手……新人工智能时代在带给我们惊喜与感慨的同时,让我们不禁想揭开其原理的神秘面纱,究竟是什么让它如此强大?
2.基础数学理论的作用
其实,人工智能的许多理论在上个世纪就早已提出,囿于计算机硬件性能而迟迟不得发展。而作为其主流算法的“深度学习”,可以说是概率论与数理统计、微积分、线性代数融合的产物。借助于计算机相关理论与计算能力,让计算机能够利用数字来认识和分析世界,并作出自己的判断与决策。人工智能算法,可以说是很多数学理论的计算机学科应用。
通过微积分,我们实现了许多函数层面对数字的分析,从二维到三维再到N维空间,偏导、微分、极值等等理论发挥了重要的作用。而线性代数成为了我们进行计算的重要工具,利用矩阵、向量等理论与性质,对大量数据进行有效的分析与处理。
3.概率论与数理统计应用概述
概率论与数理统计在其中的作用却是渗透到各个方面,从偏差、方差分析以更好的拟合到计算概率以实现预测,从随机初始化以加快训练速度到正则化、归一化数据处理以避免过拟合……概率为人工智能提供随机性,为预测提供基础;而统计则对数据进行处理与分析,让结果更好的满足我们的要求,更具有普适性和一般性,以便于我们的应用。
统计学的各种理论应用之广,让人们不禁感叹人工智能就是统计学的一种应用,尽管略有片面,但统计学方法的确在人工智能领域发挥了空前的作用。
二、深度学习原理
讨论概率论与数理统计在人工智能领域的应用,就不得不先介绍深度学习的基本原理。
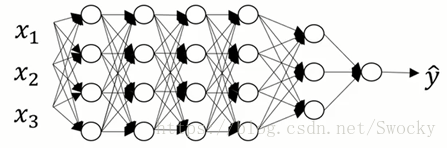
所谓深度学习,其实就是通过深层的神经网络对数据进行学习。而深层则是指隐层在两层及以上的神经网络。而单隐层的情况,则是我们所说的浅层神经网络。
可以发现,神经网络便是对输入的向量进行多层的处理,得到最终的结果。
而我们要做的,则是通过输入向量计算得到最佳的各层参数(包括权重和偏差)以实现对数据的拟合。拟合的方法,我们采用通过y ̂与真实的y进行计算数据差异,得到损失值,然后反向传播计算偏导求得梯度,通过梯度下降的方法逐渐逼近损失值的最小值。
三、概率论与深度学习
1.深度学习中的随机事件
随机事件在深度学习中有很多体现,例如随机初始化和Dropout正则化方法。
当训练神经网络时,权重随机初始化是很重要的,如果把权重或者参数都初始化为0,那么梯度下降会不起作用。简单的说,由于权重均为0,导致对称的操作造成输出结果相同,所以无论多少层都无法正确拟合。所以我们需要随机初始化。通常,我们可以通过正态分布进行随机初始化,经测试具有比较好的效果。
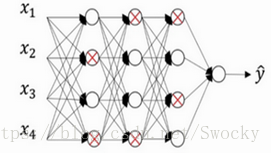
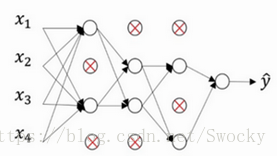
而Dropout正则化方法,则是为了防止过拟合进行的随机权重失效。每个神经元都有失效的可能性,这种随机事件会使结果更具一般性。通过随机失活,我们得到了一个更小规模的神经网络,但其对于其他数据的普适性会更好,而不会过分拟合训练样本。
显然,从这两个例子可以看出,随机性事件让我们的结果更具一般性,也能够加速我们的训练过程,避免没有必要的计算。
2.基于概率的预测分析
深度学习很重要的应用便是对数据进行分析和预测。而既然是预测,可能的结果自然不止一个,或者说每个结果都有发生的概率,而我们需要做的便是寻找概率最高的事件。
这里不得不提到Softmax回归的方法,它能够在试图识别某一分类时做出预测,不只是两个分类。假设最后的输出层是一个四维向量,对应着四种可能性,我们对于输出的z[l]计算 t=ez[l],然后得到.
![a([l])=e(z^([l]) )/(∑_(j=1)^4▒t_i )](https://img-blog.csdn.net/20181002212720388?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1N3b2NreQ==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)
显然,a [l]大于等于0且小于等于1。同样通过梯度下降进行学习,我们通过得到的参数能够预测各种结果的概率。
另外,我们通过测试集往往可以通过大量的数据中预测成功的频率来估计概率,从而评价我们的训练的模型的成功率。
除了以上算法,深度学习中的贝叶斯决策等也源于概率论。
3.概率分布的应用
深度学习很重要的一个应用便是实现预测。例如预测图中是否存在一只猫,或者预测用户是否会购买某样东西。显然,这是一个二元问题。二元问题分布的模拟便是概率论中的伯努利分布。而多元问题,很多时候我们采用的是正态分布来模拟。
概率分布更常见的应用在于权重矩阵的初始化,经测试,以正态分布来初始化能加快学习速度,所以作为初始化的常用方法之一。
四、统计学与深度学习
1.拟合
深度学习的核心原理某种意义上可以用拟合来代替,通过多层网络、多神经元以及激活函数构建一个计算图,并通过对样本的学习进行拟合,从而求得较好的参数集。得到训练好的模型后,便可以通过代入计算进行决策。
而拟合,则是统计学的一个重要内容。我们熟知的线性回归中的最小二乘法便是一种线性拟合方式,这种统计学中利用已有数据对未知数据进行判断和决策的思想,很好的应用在了深度学习中。所谓神经网络,可以说是应用于复杂数据的一种复杂的拟合方式。而统计学中很多概念如无偏估计、有偏估计同样应用在了拟合的优化中。
2.偏差与方差
偏差与方差是统计学中很重要的概念。例如样本标准偏差、总体标准偏差以及方差的统计学公式分别如下:
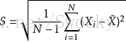
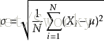
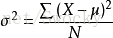
3.正则化
深度学习中的正则化是一种用来避免过拟合的方法。当我们的样本拟合程度过高时,如上文所述,会降低模型的普适性,而正则化则是用来降低过拟合问题。除了之前提到的Dropout正则化方法,L2正则化也是很常见的正则化类型。将L2正则化项
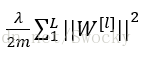
5.归一化
归一化是一种数据处理方式,广泛应用与各个学科。能将数据的某种绝对值变成相对值,有效的缩小量值并简化计算。通过归一化,能够使输入的特征值均值为0,方差为1,从而可以加速学习。
另一方面,归一化能够有效的去除一些“特性”的干扰,从而提高模型的一般性,找到数据的核心特征。而归一化方法本身,就与统计学中的均值与方差关系密切,同样也是统计学在深度学习的重大应用。
五、小结
作为基础数学,概率论与数理统计中的很多基础理论在人工智能领域都有着重要的应用。打破了硬件性能的局限,很多统计学的大规模数据处理得到了有效的实现。并且,当今人工智能领域很多创新性算法的核心也源于对于统计学知识的进一步应用。
从我们上面的讨论,无不看出概率与统计在人工智能领域各种算法中的应用与其关键性。无论是数据的处理还是分析,数据的拟合还是决策,概率与统计都提供了重要支持。
概率与统计由于其源于生活与生产,又能有效的应用于生活与生产,且应用面十分广泛。除了生活中的各类问题,在前沿的人工智能领域,同样有着重大的作用。
人类所生活的世界充满着信息与数据,如何有效的利用这些数据为人类服务,这显然是一个能有效提高生产力的课题。计算机科学中应用概率与统计的相关知识,挖掘其价值,让经典数学在人工智领域发挥着经久不息的力量。
六、参考文献
[1] 黄海广. 深度学习课程笔记[EB/OL]. https://github.com/fengdu78/deeplearning_ai_books.
[2] man_world. 指数加权移动平均(Exponential Weighted Moving Average)[EB/OL]. https://blog.csdn.net/mzpmzk/article/details/80085929.
[3] Acjx. 机器学习之正则化(Regularization)[EB/OL]. https://www.cnblogs.com/jianxinzhou/p/4083921.html.
[4] 洪亮劼. 为什么人工智能时代我们要学好概率统计?[EB/OL]. https://www.sohu.com/a/199864004_99986943.
这篇关于【个人总结】概率论与数理统计在人工智能领域的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!