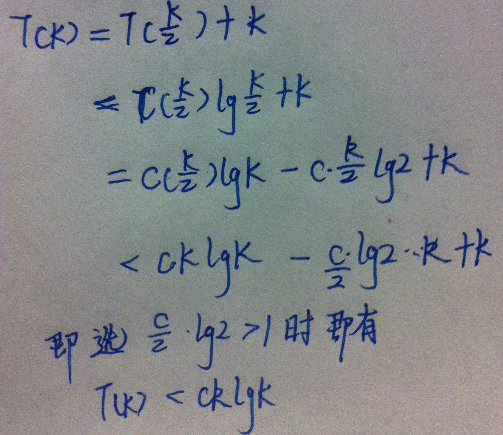数学原理专题
UF_VEC3_affine_comb函数的数学原理
double* Point1=(double *)malloc(3*sizeof(double)); double dir_r=sqrt(Dir[0]*Dir[0]+Dir[1]*Dir[1]+Dir[2]*Dir[2]); double h=80/dir_r; UF_VEC3_affine_comb(Point ,h,Dir,Point1);
DIFFUSION 系列笔记| Latent Diffusion Model、Stable Diffusion基础概念、数学原理、代码分析、案例展示
目录 Latent Diffusion Model LDM 主要思想 LDM使用示例 LDM Pipeline LDM 中的 UNET 准备时间步 time steps 预处理阶段 pre-process 下采样过程 down sampling 中间处理 mid processing 上采样 upsampling 后处理 post-process LDM Super
【通俗理解】深度学习特征提取——Attention机制的数学原理与应用
【通俗理解】深度学习特征提取——Attention机制的数学原理与应用 关键词提炼 #深度学习 #特征提取 #Attention机制 #CNN #Transformer #关联特征 #MLP #拟合处理 第一节:Attention机制的类比与核心概念 1.1 Attention机制的类比 Attention机制可以被视为一个“特征筛选器”,它像是一个精细的筛子,在众多的特征中筛选出
数学基础 -- 均方误差(Mean Squared Error, MSE)与交叉熵(Cross-Entropy)的数学原理
均方误差(Mean Squared Error, MSE)与交叉熵(Cross-Entropy)的数学原理 1. 均方误差(Mean Squared Error, MSE) 均方误差主要用于回归问题,度量预测值与实际值之间的平均平方差。其数学公式为: MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i
▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch5 蒙特卡洛方法【model-based ——> model-free】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 + 学堂在线 习题 2、 过 电子书 是否遗漏 【下载:本章 PDF GitHub 页面链接 】 【第二轮 才整理的,忘光了。。。又看了一遍视频】 3、 过 MOOC 习题 看 PDF 迷迷糊糊, 恍恍惚惚。 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【Gi
▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch4 值迭代 与 策略迭代 【动态规划 model-based】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 + 学堂在线 习题 2、过 电子书 补充 【下载: 本章 PDF 电子书 GitHub】 [又看了一遍视频。原来第一次跳过了好多内容。。。] 3、总体 MOOC 过一遍 习题 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【GitHub 链接】 总述:
▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch4 值迭代 与 策略迭代 【动态规划 算法】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 + 学堂在线 习题 2、过 电子书 补充 【下载: 本章 PDF 电子书 GitHub】 [又看了一遍视频。原来第一次跳过了好多内容。。。] 3、总体 MOOC 过一遍 习题 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【GitHub 链接】 总述:
⭐ ▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch3 贝尔曼最优公式 【压缩映射定理】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 + 学堂在线 习题 2、过 电子书,补充 【下载:本章 PDF 电子书 GitHub 界面链接】 [又看了一遍视频] 3、总体 MOOC 过一遍 习题 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【GitHub 链接】 强化学习的最终目标: 寻求最优策略
▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch2 贝尔曼公式
PPT 截取有用信息。 课程网站做习题。总体 MOOC 过一遍 1、学堂在线 视频 + 习题 2、相应章节 过电子书 复习 GitHub界面链接 3、总体 MOOC 过一遍 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【github链接】 onedrive链接: 【书】 【课程PPT】 文章目录 计算 return方法一:
From self-attention 2 flash-attention 数学原理与 cuda 实现优化
self attension 是transformer 编码器和解码器中共同的一个计算环节,在整个transformer 网络体系中耗费的算力比例占主导。所以节省self attention 的正向和反向的计算时间,就可以加速 transormer 的训练和推理过程。 1,self attention 的数学提炼 两个矩阵乘法,加入一个列向的softmax input 矩阵: o
最大整除子集——动态规划与数学原理结合
给出一个由无重复的正整数组成的集合, 找出其中最大的整除子集, 子集中任意一对 (Si, Sj) 都要满足: Si % Sj = 0 或 Sj % Si = 0。 如果有多个目标子集,返回其中任何一个均可。 示例 1: 集合: [1,2,3] 结果: [1,2] (当然, [1,3] 也正确) 直觉告诉我先排个序是很稳的,但是一般动态规划都是计算什么解的长度,解的最大最小值之类的,突然要
西湖大学赵世钰老师【强化学习的数学原理】学习笔记1节
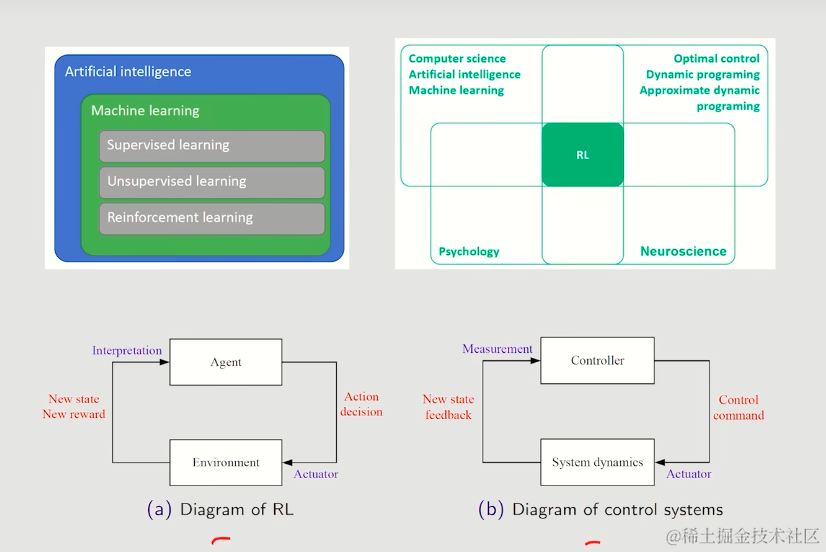
强化学习的数学原理是由西湖大学赵世钰老师带来的关于RL理论方面的详细课程,本课程深入浅出地介绍了RL的基础原理,前置技能只需要基础的编程能力、概率论以及一部分的高等数学,你听完之后会在大脑里面清晰的勾勒出RL公式推导链条中的每一个部分。赵老师明确知道RL创新研究的理论门槛在哪,也知道视频前的你我距离这个门槛还有多远。 本笔记将会用于记录我学习中的理解,会结合赵老师的视频截图,以及PDF文
西湖大学赵世钰老师【强化学习的数学原理】学习笔记2节
强化学习的数学原理是由西湖大学赵世钰老师带来的关于RL理论方面的详细课程,本课程深入浅出地介绍了RL的基础原理,前置技能只需要基础的编程能力、概率论以及一部分的高等数学,你听完之后会在大脑里面清晰的勾勒出RL公式推导链条中的每一个部分。赵老师明确知道RL创新研究的理论门槛在哪,也知道视频前的你我距离这个门槛还有多远。 本笔记将会用于记录我学习中的理解,会结合赵老师的视频截图,以及PDF文
西湖大学赵世钰老师【强化学习的数学原理】学习笔记-1、0节
强化学习的数学原理是由西湖大学赵世钰老师带来的关于RL理论方面的详细课程,本课程深入浅出地介绍了RL的基础原理,前置技能只需要基础的编程能力、概率论以及一部分的高等数学,你听完之后会在大脑里面清晰的勾勒出RL公式推导链条中的每一个部分。赵老师明确知道RL创新研究的理论门槛在哪,也知道视频前的你我距离这个门槛还有多远。 本笔记将会用于记录我学习中的理解,会结合赵老师的视频截图,以及PDF文
数学原理之机器学习中的梯度概念
导数: 一个函数在某一点的导数描述了这个函数在这一点附近的变化趋势和变化率,以物体的上抛运行为例,其(位置-时间),(速度-时间),以及(加速度-时间)的曲线可以用下图表示: 其中(速度-时间)曲线是(位置-时间)曲线在每一点的导数的值的集合,同样道理,(加速度-时间)曲线是由(速度-时间)求导得到。 以图为例,一开始,位置的变化率比较快,反映的是速度曲线的速度值比较大,随着时间推进,位置曲
算法复杂度精讲——算法时间复杂度的数学原理:从O(n(log(n))说起
概述:在设计算法的时候,要考虑两个方面,一个是算法的正确性,另外一个就是算法的效率,也就是复杂度,通常情况下,我们优先考虑的是时间复杂度,这也是本文要讨论的内容。算法学习的时候,经常碰到这样的问题,为什么快速排序的时间复杂度是O(nlog(n))?为何插入排序的时间复杂度是O(n^2)?这些是我们熟悉的算法时间复杂度,可能病没有太大的问题,那我们不熟悉的呢?如果我们采用三路归并排序而不是二路归并排
CSS3——CSS3矩阵matrix进行2D变换的数学原理
css3的2D转换中matrix接受6个参数,却可以实现平移、旋转、放缩、斜切四种效果。它是如何做到的呢? 此处的你有两个选择 0 - 对自己有较高要求!老老实实静下心来将本文看完, 1 - 直接看总结——点我直达,只学习如何使用matrix 预备知识:矩阵相乘、三角函数,fighting! 此处附上矩阵相乘的百度百科定义 我们先将matrix接受的六个参数记为a,b,c,d,e,f,则该
【强化学习的数学原理-赵世钰】课程笔记(九)策略梯度方法(Policy Gradient Method)
目录 一.policy gradient 的基本思路(Basic idea of policy gradient) 二.定义最优策略的 metrics,也就是 objective function 是什么 三.objective function 的 gradient 四.梯度上升算法(REINFORCE) 五.总结 上节课介绍了 value function approxim
一文读懂梯度下降背后的数学原理几何
来源:AI科技评论 本文共3600字,建议阅读10+分钟。 数学原理拆解+简单的现实案例,带你领略梯度下降的数学之美! 对于诸位“MLer”而言,梯度下降这个概念一定不陌生,然而从直观上来看,梯度下降的复杂性无疑也会让人“敬而远之”。本文作者 Suraj Bansal 通过对梯度下降背后的数学原理进行拆解,并配之以简单的现实案例,以轻松而有趣的口吻带大家深入了解梯度下降这一在机器学习领域至关
【强化学习的数学原理-赵世钰】课程笔记(二)贝尔曼公式
【强化学习的数学原理-赵世钰】课程笔记(二)贝尔曼公式 一. 内容概述 1. 第二章主要有两个内容 (1)一个核心概念:状态值(state value):从一个状态出发,沿着一个策略我所得到的奖励回报的平均值。状态值越高,说明对应的策略越好。之所以关注状态值,是因为它能评价一个策略的好坏。 (2)基本工具:贝尔曼公式(the Bellman equation): 用于分析状态值,描述所有
【强化学习的数学原理-赵世钰】课程笔记(一)基本概念
目录 一. 内容概述1. 通过案例介绍强化学习中的基本概念2. 在马尔可夫决策过程(MDP)的框架下将概念正式描述出来 二. 通过案例介绍强化学习中的基本概念1. 网格世界(A grid world example)2. 状态(State)3. 动作(Action)4. 状态转移(State transition)5. 策略(Policy)6. 奖励(Reward)7. 轨迹和收益(Traj
卷积神经网络(CNN)的数学原理解析
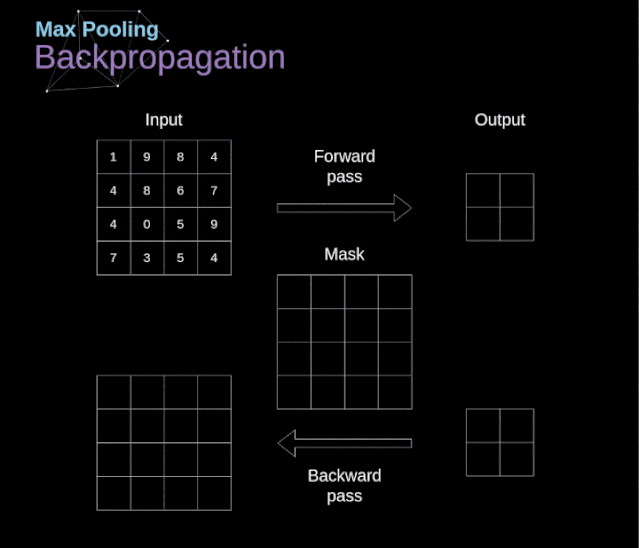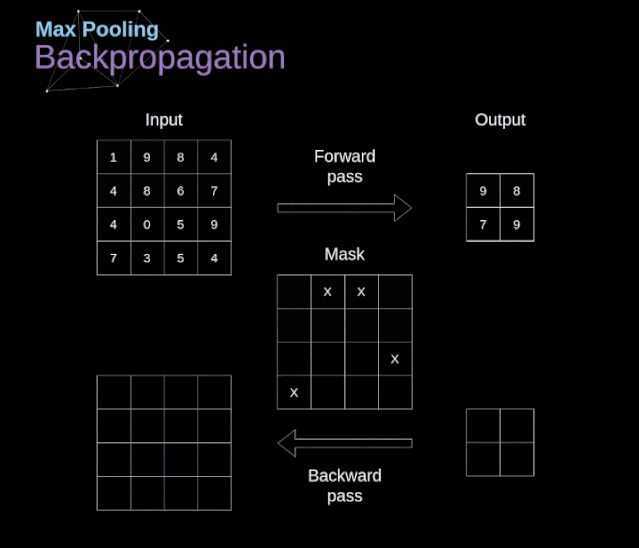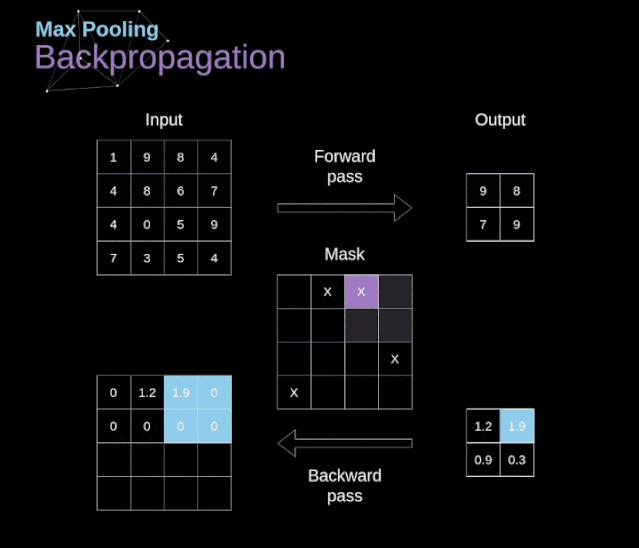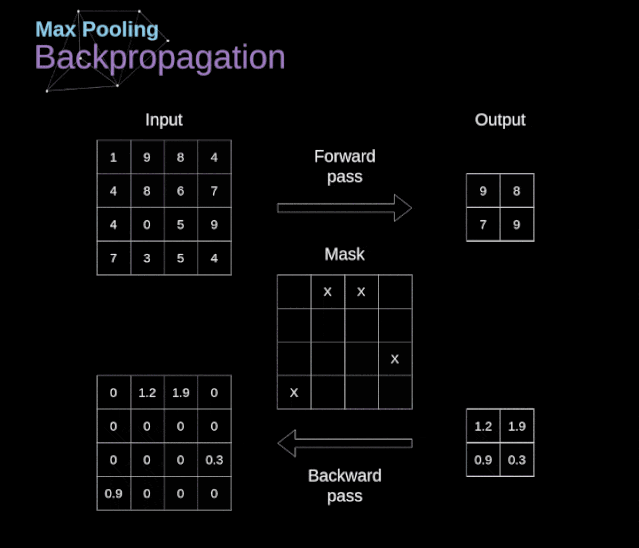
文章目录 前言 1、介绍 2、数字图像的数据结构 3、卷积 4、Valid 和 Same 卷积 5、步幅卷积 6、过渡到三维 7、卷积层 8、连接剪枝和参数共享 9、卷积反向传播 10、池化层 11、池化层反向传播 前言 本篇主要分享卷积神经网络(CNN)的数学原理解析,会让你加深理解神经网络如何工作于CNNs。出于建议,这篇文章将包含相当复杂的数学方程,如果你不习惯线性代数
理解Harris角点检测的数学原理
Harris角点检测的数学原理 Harris角点检测基于图像的局部自相似性,它通过分析图像窗口在各个方向上移动时灰度变化的程度来识别角点,它通过计算每个像素点的Harris响应值来评估该点是否为角点。数学上,这种变化可以通过构建一个二次型函数来量化,该函数基于图像在x和y方向上的一阶导数(即图像的梯度),以及梯度的二次项的组合。 一、数学题目第一题 假设我们有一个图像区域的灰度函数 I (
数学之美系列二十二 由电视剧“暗算”所想到的 — 谈谈密码学的数学原理
前一阵子看了电视剧“暗算”,蛮喜欢它的构思和里面的表演。其中有一个故事提到了密码学,故事本身不错,但是有点故弄玄虚。不过有一点是对的,就是当今的密码学是以数学为基础的。(没有看过暗算的读者可以看一下介绍, http://ent.sina.com.cn/v/2005-10-17/ba866985.shtml 因为我们后面要多次提到这部电视剧。) 密码学的历史大致可以推早到两千年前,相传名将
【强化学习的数学原理-赵世钰】课程笔记(七)时序差分方法
一.内容概述 第五节课蒙特卡洛(Mento Carlo)方法是全课程中第一次介绍 model-free 的方法,本节课的 Temporal-difference learning(TD learning)是我们要介绍的第二种 model-free 的方法。基于蒙特卡洛(Mento Carlo)的方法是一种非递增(non-incremental)的方法,Temporal-difference le