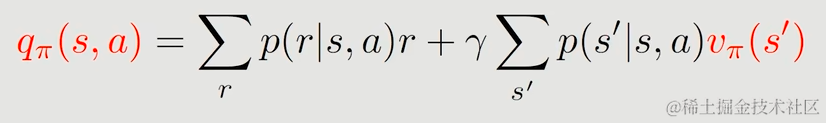本文主要是介绍西湖大学赵世钰老师【强化学习的数学原理】学习笔记2节,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
强化学习的数学原理是由西湖大学赵世钰老师带来的关于RL理论方面的详细课程,本课程深入浅出地介绍了RL的基础原理,前置技能只需要基础的编程能力、概率论以及一部分的高等数学,你听完之后会在大脑里面清晰的勾勒出RL公式推导链条中的每一个部分。赵老师明确知道RL创新研究的理论门槛在哪,也知道视频前的你我距离这个门槛还有多远。
本笔记将会用于记录我学习中的理解,会结合赵老师的视频截图,以及PDF文档Book-Mathematical-Foundation-of-Reinforcement-Learning进行笔记注释,之后也会补充课程相关的代码样例,帮助大家理解
笔记合集链接(排版更好哦🧐):《RL的数学原理》
记得点赞哟(๑ゝω╹๑)
- State-Value除了表示状态的价值大小以外,也是判断这个状态好坏的标准
Q:return和state-value的关系是什么?
A:return是对单个trajectory求得,而state-value是对多个trajectory求return再平均,当我们从一个state出发,能够产生多个trajectory时,两者就出现了差别。

3. Bellman euation:Derivation
贝尔曼公式描述了不同的state-value之间的关系

首先,我们现将Gt同之前的V一样分解两个部分,本阶段的即时奖励Rt+1,与γ相乘的下一个阶段以后的Gt+1,随后把期望拆分为两个式子,我们将分别讨论该如何计算。
3.1. 第一项

首先补充一个知识点:条件期望与全期望公式
我们对第一个式子继续进行拆分:
- 由于在当前state
s可以有多个不同的action达成后一个RewardRt+1(即均为离散型随机变量),因此可以拆出状态s条件下所有动作a的策略概率与对应条件期望(值)的乘积之和。 - 而对于同样的状态
s和动作a,所产生的奖励r同样会有所不同(即也均为离散型随机变量),因此又可以拆分出在态s和动作a的条件下的所有奖励r的概率与对应期望(只剩下r了)的乘积之和
第一项得到了immediate reward的一个mean(expectation),即立即奖励的期望
3.2. 第二项

- 从当前s出发,我们将下一个可能到达的状态称为s’,由于依然离散,我们再一次拆分出s转移到s’的概率和对应条件下的期望
- 又根据马尔科夫性质,我们发现
St=s这一条件信息是没有价值的,将其省略 - 此时的期望恰好就是
s'状态下的state_value - 最后我们再根据所采取的不同动作,再进行一次分解
第二项得到了future rewards的一个期望
3.3. 合并以及进一步推导


贝尔曼公式链接了状态之间的state-value
其包含了即时奖励与未来奖励
对状态空间中所有的状态都成了,即有n个状态,就会有n个式子,从而能够解方程获得state_value
现在,方程中的未知数是各个Vπ(S),为了求解他们,我们需要明确其余参数的值
π(a|s)就是一个给定的策略p(r|s,a)``p(s'|s,a)则是在环境中所给出的信息,但是无论知道与否,我们都有求解state_value的方法(未知的时候,称为model-free reinforcement learning算法)
3.3.1. Policy1




3.3.2. Policy2


最后发现Vπ(s4)``Vπ(s3)``Vπ(s2)都同样为10,但Vπ(s1)为8.5<9,因此策略一更好
4. Bellman equation:Matrix-vector form

为了求解贝尔曼方程,我们需要用所有状态的等式,组成方程组,于是加入了线性代数的逻辑形式,引入矩阵向量形式
虽然前面好不容易才拆开,接着就又要合上啦🙃
- 首先我们将括号中前一项取出,相乘化简,其实际意义是计算从状态s出发,按照策略π的概率选择动作a,所带来的即时奖励reward的平均
- 随后是另一项,它的实际意义是将
在状态s,通过动作a,到达状态s'的概率×在状态s,按照策略选择动作a的概率,获得了从状态s到状态s'的总概率 - 然后我们就会获得一个相对简单一些的式子


Vπ=rπ+γPπVπ
4.1. 两个policy的例子


5. Bellman euation:Solve the state values
Q:为什么要求解贝尔曼公式?
A:求解贝尔曼公式,进而获得state-value才能够实现policy-evaluation
我们将先前的等式进行一次变化,对I-γPπ 取逆

关于I-γPπ 的证明见下(本蒟蒻没有看懂)

但是在实际当中,当状态空间比较大是,求逆矩阵的运算量过大,因此更加常用的方式是迭代(iteration)


通过对有限数量的公式反复迭代后,我们可以发现Vk最终将近似于Vπ
通过极限推导可以证明δ->0
5.1. 两个好策略的例子
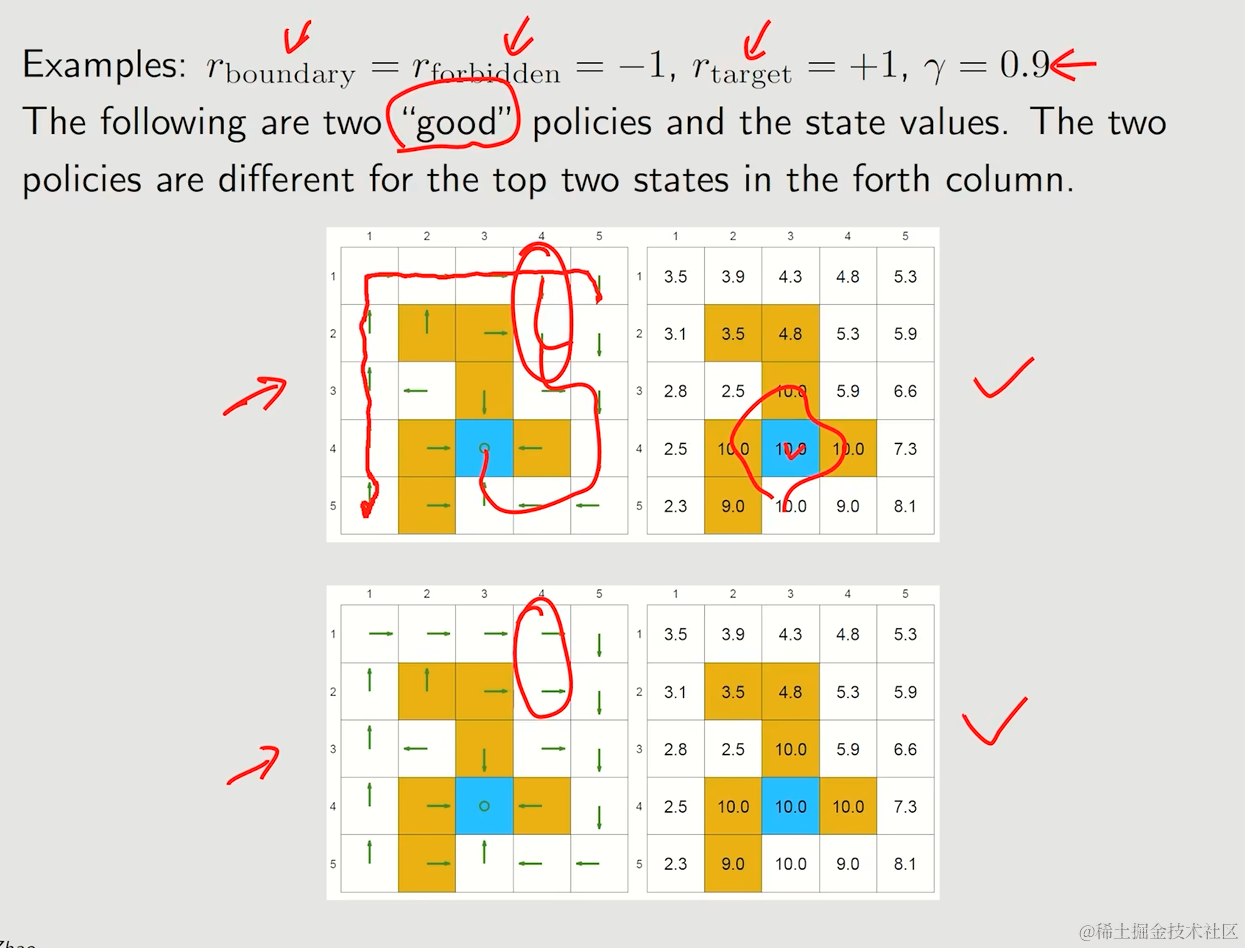
体现出的特征有:
- 所有state values均为正数
- 靠近target-area的state value会越大,反之则会越小
- 不同的policy能够产生相同的state value
5.2. 两个坏策略的例子
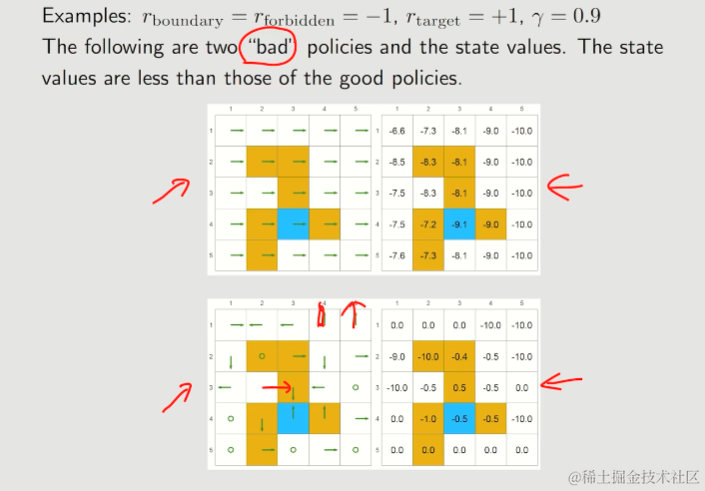
体现出的特征有:
- 所有state values均为负数
state value可以用来判断policy的好坏
6. ✨Action value
- state value指agent从一个状态出发,所得到的average return
- action value指agent从一个状态出发,并且选择了一个action之后,所得到的average return
根据action value更高的action来获得更高的reward
我们使用qπ(s,a)来表示Action value
qπ(s,a)是(s,a)的函数(由s和a共同决定)qπ(s,a)同样依赖于策略π,因为不同的策略导致的action的期望并不相通

6.1. Example
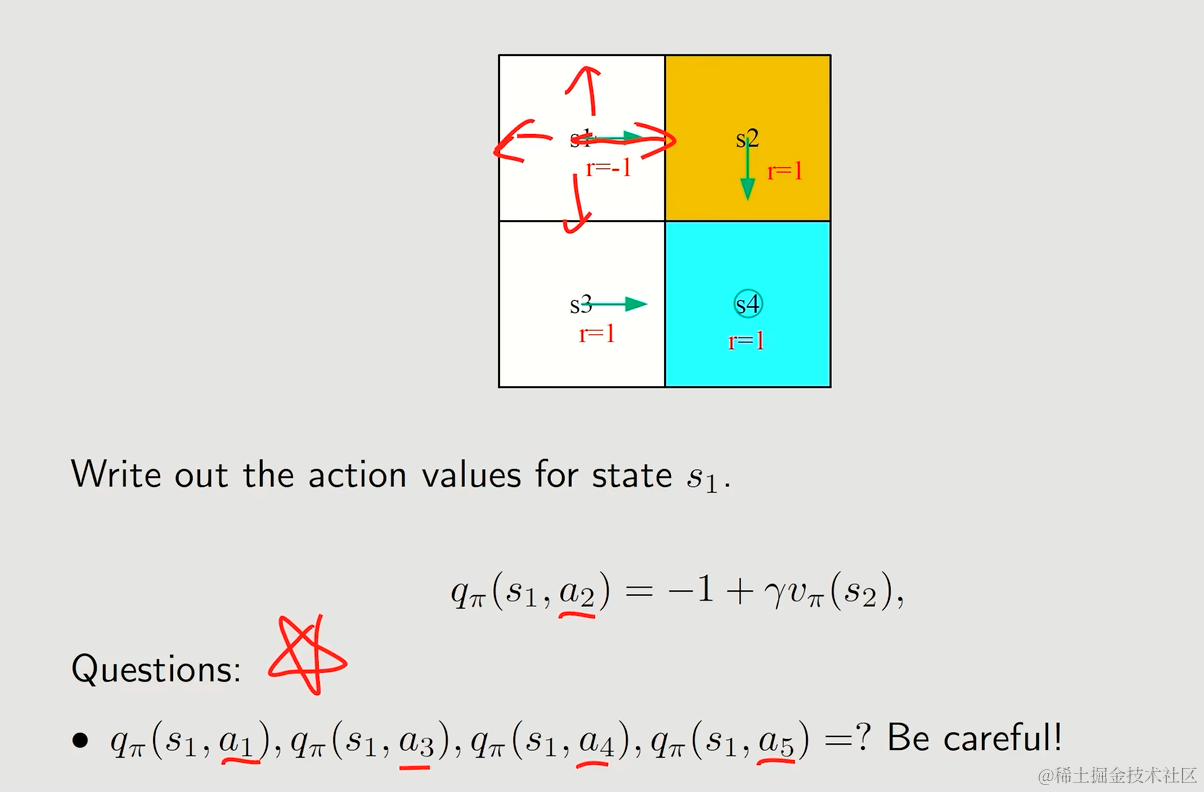

- Action value直接决定了我们选择哪一种action
- 可以通过state value以贝尔曼公式推出action value,或是通过数据直接计算(不依赖模型)
7. Summary

- 本节主要讲述了State value与Action value
- 贝尔曼公式描述了State value之间的关系,并提供了一种求解的工具,另外右联立起了State value与Action value
- 我们还介绍了贝尔曼公式的矩阵形式
- 两种求解贝尔曼公式的方法:closed-form solution(矩阵求解法),iterative solution(迭代法)
这篇关于西湖大学赵世钰老师【强化学习的数学原理】学习笔记2节的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!