悖论专题
罗素悖论 是集合论中的一个经典悖论
罗素悖论(Russell’s Paradox)是集合论中的一个经典悖论,揭示了某些集合定义的矛盾。悖论的核心是这样的:考虑一个集合,包含所有不包含自身作为元素的集合。假设这个集合是 ( R ),那么如果 ( R ) 包含自身,它就不应该包含自身;但如果 ( R ) 不包含自身,它又应该包含自身。这个矛盾显示了集合论中的一些基本假设的问题。这个悖论促使集合论的发展,引入了更严格的公理系统,如 ZFC
营销堆砌、智能悖论,褪去流量外衣后,usmile笑容加还剩下什么?
撰稿|行星 来源|贝多财经 今年的天猫“618”购物节,口腔护理品牌usmile笑容加火力全开,在渠道竞争中守擂成功,摘得等多个电商平台类目榜单桂冠,并成为天猫“618”开门红个护TOP10销售榜单上,唯一一个口腔护理品牌。 成立于2015年的usmile仅用了数年就高调走上行业牌桌,通过一系列的发展战略助推电动牙刷市场“大洗牌”,占领市场高地。但在独占细分赛道鳌头的同时,usmile“网红
从0开始学统计-蒙彼利埃尔悖论与条件概率
1.什么叫均衡可比? "均衡可比"指的是在进行比较时,确保所比较的对象或情况具有相似的特征和条件,以保持比较的公正性和准确性。这个概念通常应用于研究设计和数据分析中,以确保比较结果的可信度和有效性。 在研究中,如果要比较不同群体、不同条件或不同情况之间的影响或效果,就需要确保它们具有相似的特征和条件,以避免混杂因素的影响。只有在比较的对象之间存在相似性时,才能更准确地评估所比较的变量对结果的影
从“微积分”角度--话谈“芝诺悖论-阿基里斯与龟”
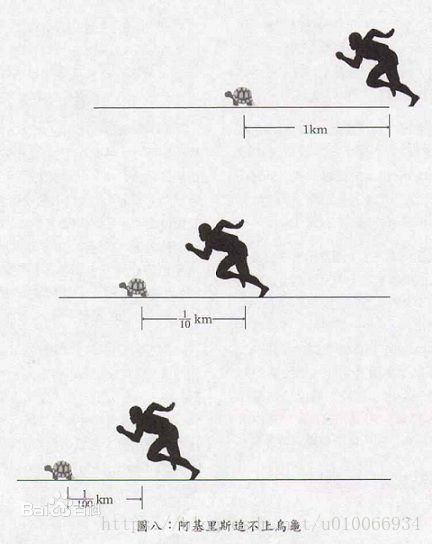
阿基里斯(又名阿喀琉斯)是古希腊神话中善跑的英雄。在他和乌龟的竞赛中,他速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他不可能追上乌龟。因为在竞赛中,追者首先必须到达被追者的出发点,当阿喀琉斯追到100米时,乌龟已经又向前爬了10米,于是,一个新的起点产生了;阿喀琉斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿喀琉斯只能再追向那个1米。就这样,乌龟会制造出无穷个起点,
关于集合悖论的通俗理解
集合分为两类,第一类集合的特征是: 集合本身又是集合中的元素。 属于第一类的例如:所有集合所组成的集合,应该是一个递归定义,具有自吞性: 第二类集合的特征是,集合本身不是集合的元素,属于第二类的例如:直线上点的集合,所有的男人的集合等等,这种没有自吞性的形式比较普遍: OK,问题来了,如果现在有一个集合A,是所有第二类集合构成的集合,也就是其集合中的元素本身也是集合,而且这个集合
林浩然的“芝诺悖论大作战”
林浩然的“芝诺悖论大作战” Lin Haoran’s “Zeno’s Paradox Grand Battle” 在一个名叫“数学江湖”的神秘世界里,住着一位名叫林浩然的智者。他身怀绝技,尤其擅长极限剑法——这门源自微积分的绝世武学,更是破解千古谜题“芝诺悖论”的利器。 In a mysterious world known as the “Mathematics Realm
男孩女孩问题 生日悖论 三门问题
上篇文章 洗牌算法详解 讲到了验证概率算法的蒙特卡罗方法,今天聊点轻松的内容:几个和概率相关的有趣问题。 计算概率有下面两个最简单的原则: 原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现的所有结果。事件 A 发生的概率 = A 包含的样本点 / 样本空间的样本总数。 原则二、计算概率一定要明白,概率是一个连续的整体,不可以把连续的概率分割开,也就是所谓的条件概率。
国王的悖论——关于自然语言
国王的悖论 国王抓住一个小偷,对小偷说你还能说一句话,如果这句话是真话你会被砍头;如果这句话为假话你会被绞死,如果你不说话会被拉去喂鳄鱼。 小偷说我应当被绞死。 这时国王犯难了,不知道该如何处理小偷。 当我们考虑到如果小偷被绞死,小偷说的就是真话,那么小偷该被处死时,此时处于一种“错误”当中。 很容易想当然的认为小偷找到了一个可以免于死亡的方法,但是假若稍加思考便会发现这句话在
生日悖论问题——《算法导论学习笔记》
1 生日悖论问题 1.1 原始问题 一个房间里的人数必须达到多少,才能使两个人生日相同的机会达到50%?不考虑闰年情况,也就是一年按照365天来计算。 解答: 假设房间里的人数是k,我们对其进行编号:1, 2, … , k。 为简单起见,用n表示一年的天数(也就是365天),那么一个人的生日在一年中的哪一天应该是机会均等的,我们用bi表示第i个人的生日,1<=bi<
林浩然的“芝诺悖论大作战”
林浩然的“芝诺悖论大作战” Lin Haoran’s “Zeno’s Paradox Grand Battle” 在一个名叫“数学江湖”的神秘世界里,住着一位名叫林浩然的智者。他身怀绝技,尤其擅长极限剑法——这门源自微积分的绝世武学,更是破解千古谜题“芝诺悖论”的利器。 In a mysterious world known as the “Mathematics Realm
第三章-集合论 3.2-Russell 悖论(选读)
概括公理(axiom comprehension)(万有分类公理) 每个性质对应于一集合基础公理(foundation axiom) A A 是一个非空集合,AA 至少包含一个元素 x x,它要么不是集合,要么是与 AA 不同的集合 习题 (1)反证,依据定义推矛盾 (2)若两者都不成立,则有 A∈B∈A A\in B\in A定义 P(x) P(x) 恒为真,集合 {x| P(x
蒙提霍尔悖论:羊车门问题
羊车门问题(又名三门问题、蒙提霍尔悖论): 有3扇关闭的门,一扇门后停着汽车,另外两扇门后是山羊,主持人知道每扇门后是什么。参赛者首先选择一扇门。在开启它之前,主持人会从另外两扇门中打开一扇门,露出门后的山羊(也就是说主持人只能开羊门)。此时,允许参赛者更换自己的选择。问换还是不换,概率为多少。 解题 难点:我们的直觉倾向于第一轮开出车的概率为⅓,第二轮变两扇门开出车的概率为½。但
网络流量与布雷斯悖论 1160300929 郑子豪
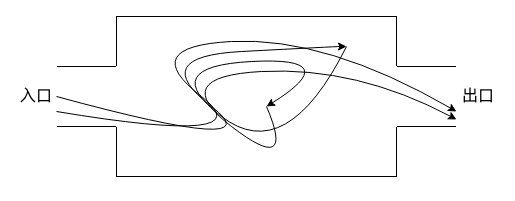
现实生活中的好多问题都可以用博弈论的知识去解释,比如在交通运输网络中行驶或者是互联网传送数据包,每个人都需要根据自己或他人的选择来对路线进行评估,最后做出最终选择。 在开车的时候,有的人觉得如果在起点和终点之间加入一些路径,会让从起点到终点的时间缩短。这是非常朴素的思维,不使用博弈论的手段进行分析的话,你可能永远都认为这是对的,实际上,在分析网络流量模型的时候,会发现一个悖论,增加网络容量可能反
世纪之争:量子物理学解决了「黑洞悖论」
在黑洞内部,20 世纪物理学的两大理论支柱似乎发生了冲突。现在,一群年轻的物理学家认为,他们通过诉诸新世纪的中心支柱——量子信息物理学,已经解决了这一冲突。 2013 年 8 月,数十位著名理论物理学家齐聚加利福尼亚州圣巴巴拉,讨论一场危机:他们对黑洞的微弱理解正在瓦解。从远处看,就像通过望远镜一样,黑洞的行为应该与行星、恒星或任何其他基本粒子的集合体一样。但是,如果物理学家们相信阿尔伯特·
【算法导论】生日悖论
生日悖论问题: 不考虑出生年份,问:一个房间中至少多少人,才能使其中两个人生日相同的概率达到50%? 解: 假设一年有 n 天,屋子中有 k 人,用整数 1, 2, …, k 对这些人进行编号。假定每个人的生日均匀分布于 n 天之中,且两个人的生日相互独立。 则,设 k 个人生日互不相同为事件A, 则事件 A 的概率为: P ( A ) = n n ∗ n − 1 n ∗ . . . ∗ n −
布雷斯悖论和借贷式拥塞控制
先看布雷斯悖论,新增一条路不但没减少交通延滞,反而降低了服务水准,下面一个简单的例子: 关于布雷斯悖论的讨论已经太多,我给出个新解释,这和我引出 借贷式拥塞控制 (差论证和编码)有关。 看一个不严谨但更简单实际(日常生活中常见)的例子: 当打通一条 “近路” 后,绝大多数流量都会自动进入近路,结果: 流量进入近路,近路上 A 处拥堵。2 处分流的假象,可能引导更多流量从 1 进入。偶
博弈论——伯特兰德悖论
伯特兰德悖论 0 引言 前面有一篇文章是关于伯特兰德寡头模型(Bertrand Model), 博弈论——伯特兰德寡头模型(Bertrand Model) 文章将伯特兰德模型与古诺模型和斯塔克尔伯格模型进行比较,这两个模型都是把厂商的产量作为竞争手段,是一种产量竞争模型,也就是说博弈方的决策变量都是产量,而伯特兰德模型是价格竞争模型,即决策变量为价格。 同时,我们在模型建立中,又提到一句话“
伯特兰悖论(Bertrand paradox)
文章目录 1. 概率中的伯特兰悖论1.1 Bertrand 对问题的表述1.2 经典解决方案1.3 Jaynes 的解决方案——使用“最大无知”原则 2. 博弈论中的伯特兰悖论 1. 概率中的伯特兰悖论 伯特兰悖论(Bertrand paradox)是概率论经典解释中的一个问题。Joseph Bertrand 在他的著作 “Calcul des probabilités, 1
14悖论_简单故事悖论
14悖论 我最近一直很感兴趣地关注 Kent Beck(@kentbeck),David Heinemeier Hansson(@dhh)和Martin Fowler(@martinfowler)之间的#isTDDDead辩论。 我认为,可以以建设性的方式挑战通常被认为是理所当然的想法是特别有益的。 这样,您就可以确定他们是经得起审查还是跌落在脸上。 讨论从@dhh开始,就TDD
Comunion:打破后工业时代的努力与收益悖论
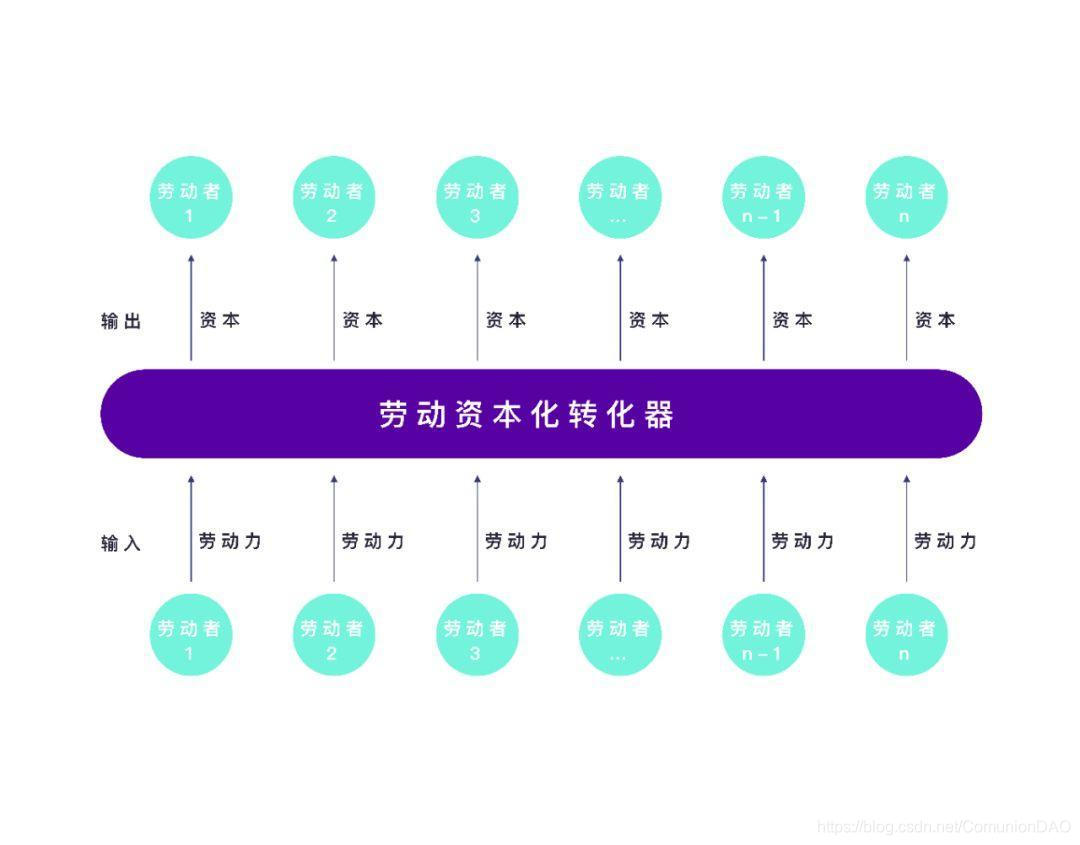
摘要 Comunion 是一个去中心化组织协作网络,旨在帮助商业公司、组织和个人创建、管理并运营去中心化组织(DAO) 。Comunion 的使命是通过重塑现有生产关系激活生产力,让全球资源实现高效分配,让劳动价值像资本一样自由流通、交易和积累。 现代性的后果 工业时代技术与生产力的大爆炸将我们卷入了现代性世界。现代性不但让我们的意识形态进入了单向度空间,也为我们带来了时空维度上的脱域,知识性
企业应如何解决云成本优化悖论?
最近一篇题为“云的成本,万亿美元悖论”的分析备受关注。这篇文章挑战了围绕云转型和云迁移狂热的传统思维,它要求我们思考云基础设施成本的影响(以及这反过来对公司估值的影响)。 也有观点指出,对于 SaaS 公司来说,云计算的成本会拖累他们的市值。 这个悖论表明,在公司发展的早期,云计算成本更低,随着公司规模的扩大,它变得更加昂贵。他们说得很简单:“如果你不从云开始,你就疯了,如果你坚持下去