本文主要是介绍布雷斯悖论和借贷式拥塞控制,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
先看布雷斯悖论,新增一条路不但没减少交通延滞,反而降低了服务水准,下面一个简单的例子:
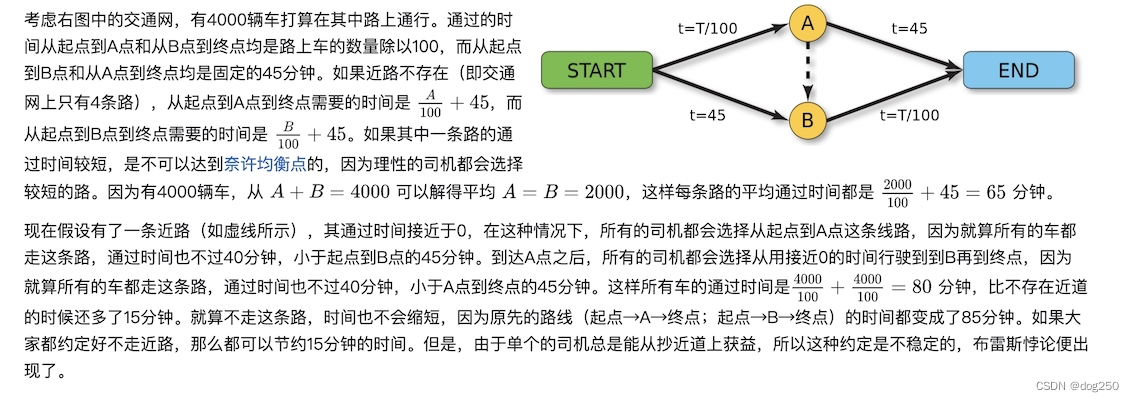
关于布雷斯悖论的讨论已经太多,我给出个新解释,这和我引出 借贷式拥塞控制 (差论证和编码)有关。
看一个不严谨但更简单实际(日常生活中常见)的例子:
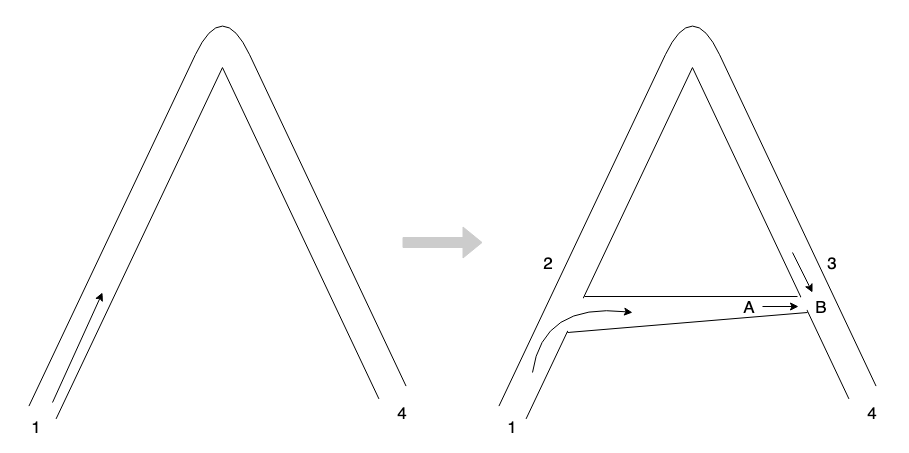
当打通一条 “近路” 后,绝大多数流量都会自动进入近路,结果:
- 流量进入近路,近路上 A 处拥堵。
- 2 处分流的假象,可能引导更多流量从 1 进入。
- 偶尔进入原始路径的流量在 3 处和近路流量汇合而拥堵。
- 如果 2 到 3 间有入口,新流量会被 2-3 间的小流量欺骗,大量涌入后在 3 处加剧拥堵。
所有这一切都因打通了 2,3 间的近路。
进一步抽象一下,将入口 1 和 4 之间的所有可能路径设想成一个纷乱如麻的黑盒子,里面塞满了所有可能的路径(这是可能的,但不容易想象):

所有这些路径有直达的,有中转的,总之这简直是 full-mesh,能连接的都连在一起。假设每条路径都有流量,以下结论是显然的:
- 总存在至少 1 条路径从入口到达出口时间最短。
- 总存在至少 1 条路径使出口满负载运转。
现在做以下操作:
- 上述第一点的那些路径加入集合 S,排除 S 外的其它路径。
- 看出口是否满负载,如果不满负载,在集合 S 外找最优路径,重复 1。
- 直到出口满负载。
集合 S 让出口满负载,这就是这个盒子的最优解:最小时延,最大带宽:
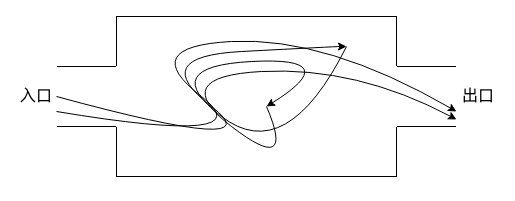
现在将那些不属于 S 的路径逐步添加进盒子,这等价于 “修路”,它的结果是:
- 出口负载已满,不会再增加。
- 入口进入的流量增加。
- 出入不守恒,盒子内部拥塞,这表示 “整个网络的服务水准下降”。
以上就是布雷斯悖论的解释。
拥塞的根本原因在于负反馈时间过久,以至入口容量的假象欺骗太久,如果盒子巨大,溢出盒子需很久,这将导入大量无效流量。容易发现,越宽的路,堵车时越壮观,无论多宽的路,似乎总是被填满。
负反馈的延迟导致正反馈:路越宽,负反馈越久,维持欺骗的时间越久,拥塞程度越剧烈。buffer 越大,拥塞越很。
若转为主观,占便宜不花代价,大家都占便宜时,自己必须趋同,整条路都被占便宜者堵着,你能怎么办,缺乏反向激励和惩罚机制。这就是我屡次强调过的,别的流通过 probe 挤兑带宽时,自己就必须用至少一样的力度挤兑,否则将一无所有。
评价车牌拍卖制度时,我们能感受到虽然本意是减缓拥塞,车牌价格相当于拥塞税,你要开车,就要花钱,因为你不花钱就没拍照,所以花钱而已,车就越来越多。这和 cubic vs. bbr 异曲同工,想获得更多带宽,只能 probe,但也就 probe 而已,buffer 越堆越满,幸好 cubic 有 aimd 约束,当然也是为了自己。
拍牌相当于提前预付拥塞税,必须交钱才能开车,既然已经交了,就随便上路了,没有 “实时的” 反向措施作为勾引或反制。比如如果不开车转而坐公共交通,会退钱。
回到上面黑盒子,如果每人进入盒子一次收 1 元,两次收 2 元,10 人合并进入一次奖励 1 元,20 人合并进入奖励 2 元,这个盒子最终会自动识别 S 集。
再回到最上面 wiki 的例子,如果近路不再 0 成本,而是第一天收 1 元,第二天收 2 元,第一天走原路奖励 1 远,第二天走原路奖励 2 元,结合时间货币成本自行考量,新路顺利提升了通行效率。
一方亏的给了另一方,让他的收益递减他才肯主动亏,因为这能换来他的收益递增。没有动机作恶才是最好的。
总之,负反馈也好,自抑制也罢,让占便宜的收益递减,不占便宜的吃亏递增,or 占便宜的惩罚递增,不占便宜的奖励递减,系统就会自动收敛到高效和公平,结合经济规律以及人口规律的周期性,这就是我那个 借贷式拥塞控制 的缘起和初衷。
aimd 和 bbr 分别处于借贷式拥塞控制的两边,aimd 预付拥塞税,却对代价零存整取,而 bbr 则试图实时跟踪并匹配资源,虽说我们不希望 cc 工作在右边的丢包点,但左边的 bltbw/proprt 最优操作点却不可达,真实情况在二者之间。
纳什均衡可能也不是最优解,但却是最平衡的。
浙江温州皮鞋湿,下雨进水不会胖。
这篇关于布雷斯悖论和借贷式拥塞控制的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




