本文主要是介绍芝诺悖论,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们先来看一下芝诺悖论的三个经典问题:
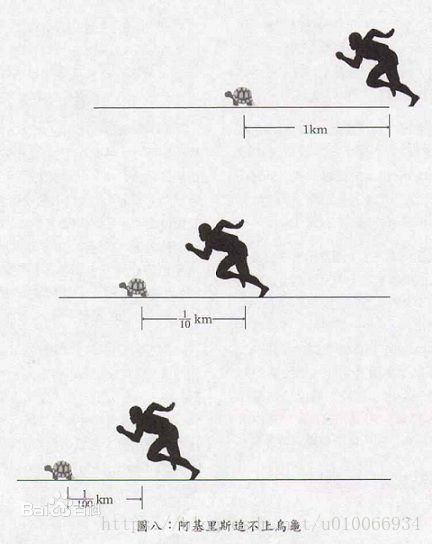
阿基里斯是古希腊神话中的跑步健将。假设他和乌龟赛跑,他速度为乌龟的10倍,乌龟在前面10米出发,他在后面追。芝诺可以证明,阿基里斯永远不可能追上乌龟:
当阿基里斯追到10米时,乌龟已经向前爬了1米;而当他追过这1米时,乌龟又已经向前爬了0.1米,他只能再追向那个0.1米。因为追赶者需要用一段时间才能达到被追者的出发点,这段时间内被追者已经又往前走了一段距离,所以被追者总是在追赶者前面。这样,阿基里斯就永远也追不上乌龟!
设想一支飞行的箭。在每一时刻,它位于空间中的一个特定位置。由于时刻无持续时间,箭在每个时刻都没有时间而只能是静止的。鉴于整个运动期间只包含时刻,而每个时刻又只有静止的箭,所以芝诺断定,飞行的箭总是静止的,它不可能在运动。
首先假设在操场上,在一瞬间(一个最小时间单位)里,相对于观众席A,列队B、C将分别各向右和左移动一个距离单位。
◆◆◆◆观众席A
▲▲▲▲队列B
▼▼▼▼队列C
B、C两个列队开始移动,如下图所示相对于观众席A,B和C分别向右和左各移动了一个距离单位。
◆◆◆◆观众席A
▲▲▲▲队列B……向右移动
▼▼▼▼队列C……向左移动
而此时,对B而言C移动了两个距离单位。也就是,队列既可以在一瞬间(一个最小时间单位)里移动一个距离单位,也可以在半个最小时间单位里移动一个距离单位,这就产生了半个时间单位等于一个时间单位的矛盾。因此队列是移动不了的。
第一个问题:时间是不可分的,时间不因为任何事暂停,不论乌龟跑了多久,或者阿基里斯跑了多久,他们不可能永远停留在无限分割的无限小的时间里。
第二个问题:速度也是不可分的,速度必定是一个时间段内的计算出来的值,假设时间停止,就没有速度,只要时间在流逝,速度就不可能是0
第三个问题:移动是相对的,参考值应该始终唯一。
虽然芝诺悖论已经被解决了,但是很多时候,猛一听,还是很有道理的,让人更感兴趣的是,在几千年前,人们就已经在开始思考这样的问题,而在现代,其实很多人一辈子都没有听说过芝诺悖论。
这篇关于芝诺悖论的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!