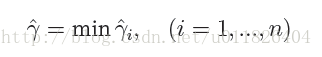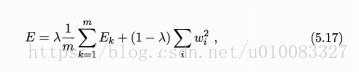周志华专题
《机器学习》周志华-CH5(神经网络)
5.1神经元模型 机器学习中谈论神经网络指“神经网络学习”。 神经网络基本成分是神经元(neuron)和模型 1943年,McCulloch and Pitts:M-P神经元模型 5.2感知机与多层网络 感知机(Perceptron)由两层神经元组成,又称“阈值逻辑单元(threshold logic unit)” 感知机可实现与、或、非运算, y =
《机器学习》周志华-CH4(决策树)
4.1基本流程 决策树是一类常见的机器学习方法,又称“判别树”,决策过程最终结论对应了我们所希望的判定结果。 一棵决策树 { 一个根结点 包含样本全集 若干个内部结点 对应属性测试,每个结点包含的样本集合根据属性测试结果划分到子结点中 若干个叶结点 对应决策结果 一棵决策树 \begin{cases} 一个根结点 &包含样本全集 \\ 若干个内部结点 & 对应属性测试,每个结点包含的样本
周志华《Machine Learning》学习笔记(7)--支持向量机
写在前面的话:距离上篇博客竟过去快一个月了,写完神经网络博客正式进入考试模式,几次考试+几篇报告下来弄得心颇不宁静了,今日定下来看到一句鸡血:Tomorrow is another due!也许生活就需要一些deadline~~ 上篇主要介绍了神经网络。首先从生物学神经元出发,引出了它的数学抽象模型–MP神经元以及由两层神经元组成的感知机模型,并基于梯度下降的方法描述了感知机模型的权值调整规则。
周志华《Machine Learning》学习笔记(6)--神经网络
上篇主要讨论了决策树算法。首先从决策树的基本概念出发,引出决策树基于树形结构进行决策,进一步介绍了构造决策树的递归流程以及其递归终止条件,在递归的过程中,划分属性的选择起到了关键作用,因此紧接着讨论了三种评估属性划分效果的经典算法,介绍了剪枝策略来解决原生决策树容易产生的过拟合问题,最后简述了属性连续值/缺失值的处理方法。本篇将讨论现阶段十分热门的另一个经典监督学习算法–神经网络(neural n
《机器学习(周志华)》Chapter5 神经网络 课后习题答案
若用线性函数作为神经元激活函数则无法处理复杂的非线性问题。 激活函数在神经网络中的作用 相当于每个神经元都在进行对率回归 学习率控制着梯度下降的搜索步长,学习率过大收敛过程容易发生振荡,学习率过小收敛速度过慢 https://blog.csdn.net/victoriaw/article/details/78075266 https://blo
《机器学习(周志华)》Chapter5 神经网络
一、神经元模型: θ为阀值,输入样本x与权重w相乘再求和若大于阀值θ则兴奋即输出为1,否则抑制输出为0,f为激活函数经典的有Sigmoid函数 二、感知机与多层网络: 感知机由两层神经元组成 若θ设置为常数,则可训练出权重w 多层前馈神经网络: 三、误差逆传播算法 称BP算法,采用链式求导法则求出各层权重及阀值的导数。 假设神经网络的输出为: 则均
《机器学习(周志华)》Chapter4 决策树 课后习题答案
由决策树生成过程可知,不含冲突数据对结点标记有两种情况,一、划分后数据集为同一类则结点标记为该类的叶节点,二、划分后数据集中的属性相同则标记为数据集中类别最多的类。这样所有属性相同的样本最终标记必定会一样,即必存在误差为0的决策树。 训练误差不一定能代表泛化误差,若以最小训练误差作为决策树划分选择准则会容易导致过拟合,泛化性能差 4.3编程实现id3 4.4编程实现C
《机器学习(周志华)》Chapter4 决策树
决策树算法比较容易理解,在这里简单做一下记录。 一、决策树: 决策树解决分类问题,简单来说就是依次选择样本属性作为结点,将该样本属性值作为叶子来展开,最终划分出的叶子标记为训练样例数最多的类别。 二、划分选择: 在选择属性的时候到底改选择哪个属性?这就引出了划分选择,选择出决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”越来越高,文中介绍了三种方式:信息增益、增益率、基
《机器学习(周志华)》Chapter3 线性模型 课后习题答案
偏置项b在数值上代表了自变量取0时,因变量的取值; 1.当讨论变量x对结果y的影响,不用考虑b; 2.可以用变量归一化(max-min或z-score)来消除偏置。 这里提供大致思路,对一元函数而言,求二阶导,如果二阶导小于零则为凸函数,否则为非凸。 若对多元函数求二阶导,需要得到Hessian矩阵,然后根据Hessian的正定性判定函数的凸凹性,比如Hessian矩阵半正定
《机器学习(周志华)》Chapter3 线性模型
本章介绍线性模型,性模型能解决哪些现实中的问题?主要有对连续数据的预测(回归问题)、二分类问题、线性判别分析(LDA)和多分类问题。 一、单变量线性回归、多变量线性回归 1、线性回归基本形式: 目的是训练出一组w和b使得y≈f(x),一般用均方误差度量即: (上式也可以理解为求数据到直线的欧式距离最小) 要求出最小值,对3.4式求导后等于零即可求出: 2、多变量线性回归
《机器学习(周志华)》Chapter2 模型评估与选择 课后习题答案
根据题意可知正例和反例各位50个样本,题目假定的算法为若训练集中正例较多则为正例,反之为反例。 1、先考虑简单的留一法: 若取得1个正例为测试集,则剩下训练集为49个正例50个反例,算法预测为反例,则与测试集预测相反。反之同样成立,则留一法的错误率为100% 2、10折交叉验证 若测试集中正例与反例各为5个,则剩下训练集为45个正例45个反例,因为训练样本数据相同时进行随机猜测
《机器学习(周志华)》Chapter2 模型评估与选择
这一章几乎把整个机器学习的工作流程都介绍了一遍,能让读者了解到如何一步步的搭建一个机器学习项目。下面先把整个流程大致的梳理一遍: 一、评估方法: 我们在拿到数据之后首先要处理的就是将数据划分为训练集和测试集,西瓜书提供了三种方法,分别是:留出法、交叉验证法和自助法。 1、留出法:将数据集划分为两个互斥的集合,将70%划分为训练集,30%划分为测试集。如果我们希望评估的是整个训练集的模
《机器学习by周志华》学习笔记-线性模型-03
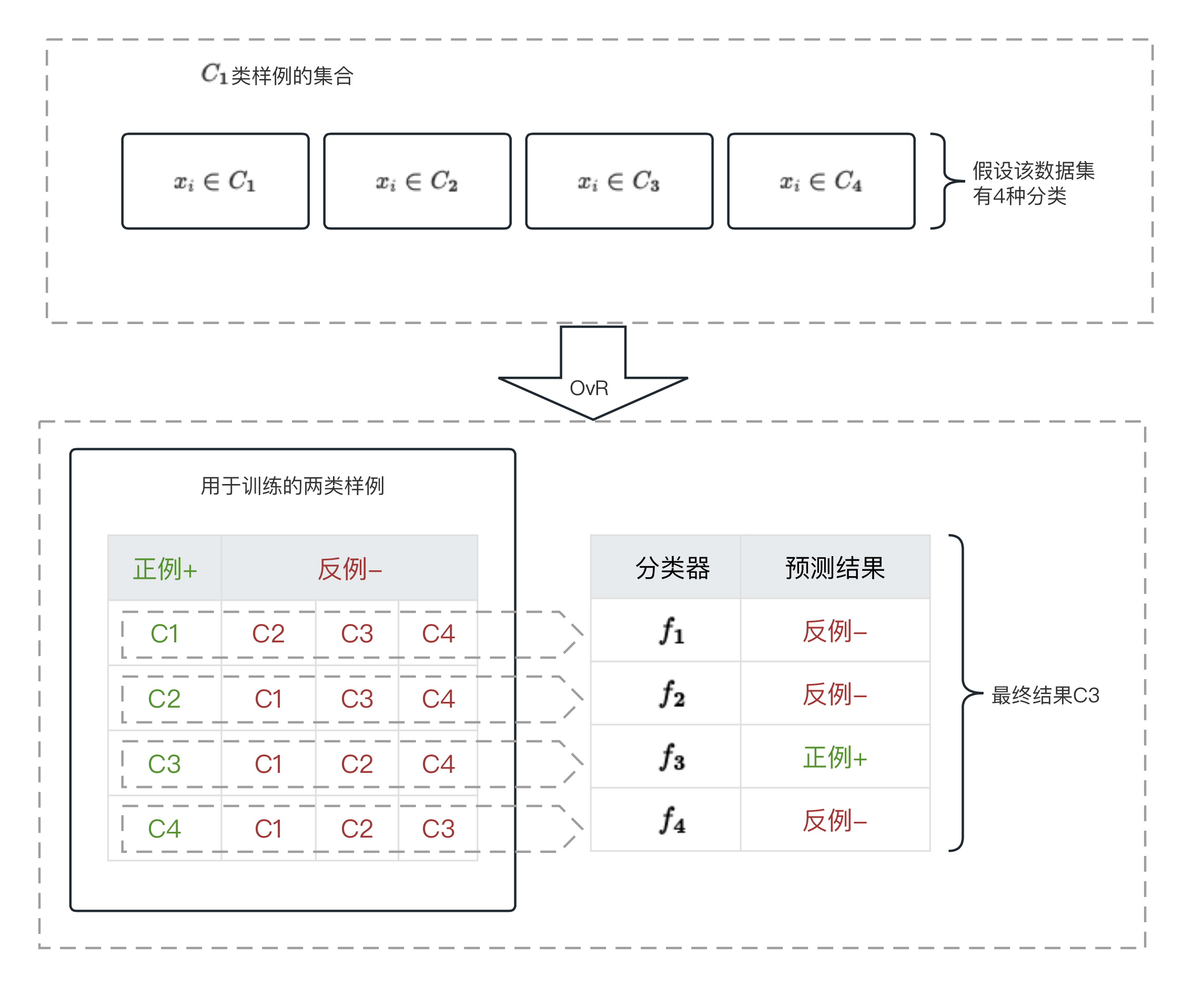
1、多分类学习 1.1、背景 我们在上一节介绍了「线性判别分析(LDA)」,LDA的从二分类任务可以推广到多分类任务中。 而现实中常遇到的多分类学习任务。有些二分类的学习方法可以直接推广到多分类,但是更多情况下是基于一些策略,利用二分类学习器来解决多分类的问题。 1.2、概念 我们通常将「分类学习器」简称「分类器(classifier)」,多个「分类器」的集成使用,则称为「集成学习」。
周志华《机器学习》算法优缺点总览
说明 本文档使用MindManager编辑: 做这个笔记的初衷是供自己快速复习查找合适的算法,基本以各算法的优缺点与条件为主,省略推导过程和公式,所以分享出来也是供《机器学习》一书的读者复习使用,或仅仅想简单了解或查找机器学习的一些常用算法及数据处理方法的读者使用;每个算法、处理方法及指标的详细说明在便笺中,若要查看需在图标上悬停或点击;此笔记是根据已购买的正版实体书手打整理,如果里面有错误之
《机器学习by周志华》学习笔记-线性模型-02
1、对数几率回归 1.1、背景 上一节我们考虑了线性模型的回归学习,但是想要做分类任务就需要用到上文中的广义线性模型。 当联系函数连续且充分光滑,考虑单调可微函数,令: 1.2、概念 找一个单调可谓函数,将分类任务的真实标记与线性回归模型的预测值联系起来,也叫做「Heaviside函数」。 在二分类任务中,输出的真实标记,而线性回归模型产生的预测值是实数值。于是我们将转化为0、1值
机器学习理论 | 周志华西瓜书 第十六章:强化学习
第十六章 强化学习 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 16.1 任务与奖赏 通常使用马尔可夫决策过程(MDP)描述目的:找到能长期积累奖赏最大化策略长期奖赏方式 T步积累奖赏: E [ 1 T ∑ t = 1 T r t ] \mathbb{E}[\frac 1 T\sum_{t=1}^Tr_t] E[T1∑t=1Trt] γ折扣积累奖赏: E [ ∑
机器学习理论 | 周志华西瓜书 第十五章:规则学习
第十五章 规则学习 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 15.1 基本概念 规则:语义明确,能描述数据分布所隐含的客观规律或领域概念规则学习:从训练数据中学习一种能用于未见示例进行判别的规则优点:有更好的可解释性、有冲突可进行冲突消解 15.2 序贯覆盖(分治策略) 原因:规则学习的目标是产生一个能覆盖尽可能多的样例的规则集,最直接做法——序贯覆盖(逐条归纳
机器学习理论 | 周志华西瓜书 第十二章:计算学习理论
第十二章 计算学习理论 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 12.1 基础知识 1、概述 目的:分析学习任务的困难本质,为学习算法提供理论保证) 2、一些定义 令h为从X到Y的映射,h的泛化误差: E ( h ; D ) = P x ∼ D ( h ( x ) ≠ y ) E(h;\mathcal{D})=P_{\bm x\sim\mathcal{D}}(h
机器学习理论 | 周志华西瓜书 第十一章:特征选择与稀疏学习
第十一章 特征选择与稀疏学习 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 11.1 子集搜索与评价 1、一些概念 特征/相关特征/无关特征 冗余特征:所包含的信息能从其他特征中推演出来(多数时候不起作用,除去以减轻学习负担,但有时会降低学习任务的难度) 2、特征选择的原因:减轻维数灾难,降低学习难度 3、特征选择方法本质 特征子集搜索机制(subset searc
机器学习理论 | 周志华西瓜书 第十章:降维与度量学习
第十章 降维与度量学习 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 10.1 k近邻学习 1、描述 常用的监督学习方法 工作机制:给定测试集,基于某距离度量找出最靠近的k个样本,基于k个邻居的信息预测 分类——投票法回归——平均法 懒惰学习的代表 2、懒惰学习与急切学习 懒惰学习(lazy study):没有显式训练过程,仅把样本保存,训练时间无开销,待收到测试
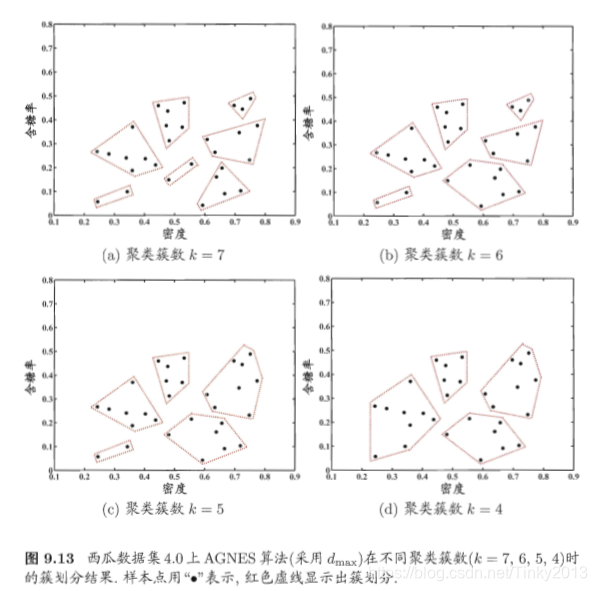
机器学习理论 | 周志华西瓜书 第九章:聚类
第九章 聚类 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 9.1 聚类任务 无监督学习:训练样本标记位置,学习揭示内在规律,分类任务等前驱过程 将数据集划分为若干互不相交的子集(簇:cluster) 9.2 性能度量 1、概念 内相似度(intra-cluster similarity)簇间相似度(inter-cluster similarity) 2、指标
机器学习理论 | 周志华西瓜书 第八章:集成学习
第八章 集成学习 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 8.1 个体与集成 集成学习的一般结构 示意图 个体学习器(individual learner) 基学习器(base learner) 同质(homogenous)集成:集成中只包含同种类型的个体学习器 基学习器——同质集成中的个体学习器 基学习算法(base learning algorithm)——相应
机器学习理论 | 周志华西瓜书 第七章:贝叶斯分类器
第七章 贝叶斯分类器 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 7.1 贝叶斯决策理论 期望损失(expected loss):在样本x上的“条件风险”(conditional risk) 具体算式: R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R(c_i|\bm x)=\sum_{j=1}^N\lambda_{ij}P
机器学习理论 | 周志华西瓜书 第六章:支持向量机
第六章 支持向量机 此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中… 6.1 间隔与支持向量 超平面(w,b) 存在多个划分超平面将两类样本分开的情况 线性方程: w T x + b = 0 w^Tx+b=0 wTx+b=0 w w w:法向量,决定超平面方向 b b b:位移项,决定超平面与原点之间的距离 样本空间中任意点到超平面的距离: r = ∣ w T x + b
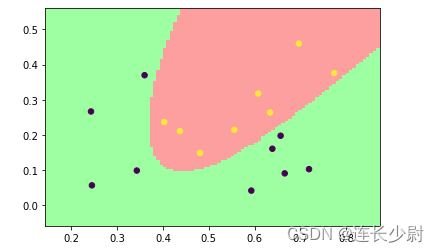
周志华《机器学习》习题6.2——使用LIBSVM比较线性核和高斯核的差别
1.题目 试使用LIBSVM,在西瓜数据集3.0α上分别用线性核和高斯核训练一个SVM,并比较其支持向量的差别。 西瓜数据集3.0α如下图: 2.LIBSVM libsvm是目前比较著名的SVM软件包,由台湾大学林智仁(Chih-Jen Lin)教授等开发,它可以帮助程序员轻松的实现SVM二分类、多分类或者SVR等任务。 LIBSVM官网:https://www.csie.ntu.edu