机器学习理论 | 周志华西瓜书 第十一章：特征选择与稀疏学习

本文主要是介绍机器学习理论 | 周志华西瓜书 第十一章：特征选择与稀疏学习，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第十一章 特征选择与稀疏学习

此系列文章旨在提炼周志华《机器学习》的核心要点，不断完善中…

---

11.1 子集搜索与评价

1、一些概念
特征/相关特征/无关特征
冗余特征：所包含的信息能从其他特征中推演出来（多数时候不起作用，除去以减轻学习负担，但有时会降低学习任务的难度）

2、特征选择的原因：减轻维数灾难，降低学习难度

3、特征选择方法本质

• 特征子集搜索机制(subset search)（贪心策略）
  前向搜索：单特征开始，每次增加一个最相关的
  后向搜索：完整开始，每次去掉一个最无关的
  双向搜索：二者结合
• 子集评价机制(subset evaluation)
  • 给定数据集D，假定D中第i类样本所占比例为$p_i(i=1,2,...,|\mathcal{Y}|)$。对属性子集A，假定根据其取值将D分成了V个子集 { D 1 , D 2 , . . . D V } \{D^1,D^2,...D^V\} {D1,D2,...DV}，每个子集中的样本在A上取值相同
  • 信息增益Gain(A)：越大表明包含有利于分类的信息越多
    信息熵定义：$Ent(D)=-{\sum }_{k=1}^{|\mathcal{Y}|}{p}_{k}lo{g}_2{p}_k$
    子集A的信息增益： $Gain(A)=Ent(D)-{\sum }_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$
  • 注意：信息熵仅是判断这个差异的一种途径，其他能判断两个划分差异的机制都能用于特征子集评价：不合度量、相关系数等

11.2 过滤式选择（不考虑后续学习器）

1、二分类问题方法：Relief

• 确定相关统计量
  猜中近邻(near-hit)：对每个示例${\mathbf{x}}_i$，在同类样本中寻找最近邻${\mathbf{x}}_{i,nh}$
  猜错近邻(near-miss)：对每个示例${\mathbf{x}}_i$，在异类样本中寻找最近邻${\mathbf{x}}_{i,nm}$

• 相关统计量对应于属性j的分量：
  $${\delta }^j=\sum _j-diff(x_i^j,x_{i,nh}^j{)}^2+diff(x_i^j,x_{i,nm}^j{)}^2$$

• Relief只需在数据集的采样上而不必在整个数据集上估计相关统计量，因此是一个运行效率很高的过滤式特征选择法

2、多分类问题方法：Relief-F

• 确定相关统计量
  $${\delta }^j=\sum _j-diff(x_i^j,x_{i,nh}^j{)}^2+\sum _{l\ne k}(p_l\ast diff(x_i^j,x_{i,l,nm}^j{)}^2)$$

11.3 包裹式选择（直接把最终将要使用的学习器的性能作为特征子集的评价准则）

1、与过滤式选择比较

• 包裹式特征选择最终学习器性能更好
• 包裹式特征选择的计算开销通常大得多

2、典型方法：LVW(Las Vegas Wrapper)

• 在拉斯维加斯方法(Las Vegas method)框架下使用随机策略来进行子集搜索，以最终分类器的误差为特征子集评价准则
• 算法：
• 若初始特征数很多（即|A|很大）、停止条件控制参数T设置较大：算法可能运行很长时间都达不到停止条件（若有时间限制可能解不出）

11.4 嵌入式选择与L1正则化（将特征选择过程与学习器训练过程融为一体）

1、基于L1正则化的学习方法——嵌入式特征选择方法

• 线性回归模型以平方误差为损失函数的优化目标：$mi{n}_{\mathbf{w}}{\sum }_{i=1}^m(y_i-{\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}{)}^2$
• 样本特征很多而样本数目相对较少时——缓解过拟合
  引入L2正则化（岭回归）：$mi{n}_{\mathbf{w}}{\sum }_{i=1}^m(y_i-{\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}{)}^2+\mathbf{\lambda }||\mathbf{w}|{|}_2^2$
  引入L1正则化（LASSO）：$mi{n}_{\mathbf{w}}{\sum }_{i=1}^m(y_i-{\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}{)}^2+\mathbf{\lambda }||\mathbf{w}|{|}_1$
• 图解
  

2、L1正则化问题的求解——近端梯度下降(Proximal Gradient Descent, PGD)

11.5 稀疏表示与字典学习

1、特征选择考虑的稀疏性问题：无关特征(矩阵中的列)与当前学习任务无关

2、另一种稀疏性问题：数据矩阵存在很多0，但并不是以整行/整列形式存在

• 1）文档分类任务：每个文档看做一个样本，每个字(词)作为一个特征，在文档中出现的频率作为特征取值（恰当稀疏 not 过度稀疏）
• 2）一般学习任务(如图像分类)——字典学习(dictionary learning)
  • 简述：为普通稠密表达的样本找到合适的字典，将样本转化为合适的稀疏表示形式，从而使学习任务得以简化，模型复杂度得以降低
  • 数学推导
    字典学习最简单形式：
    $$mi{n}_{\mathbf{B},{\mathbf{\alpha }}_{\mathbf{i}}}\sum _{i=1}^m||{\mathbf{x}}_i-\mathbf{B}{\mathbf{\alpha }}_{\mathbf{i}}|{|}_2^2+\mathbf{\lambda }\sum _{i=1}^m||{\mathbf{\alpha }}_i|{|}_1$$
    按照LASSO解法求解该式：
    $$mi{n}_{{\mathbf{\alpha }}_{\mathbf{i}}}||{\mathbf{x}}_i-\mathbf{B}{\mathbf{\alpha }}_{\mathbf{i}}|{|}_2^2+\mathbf{\lambda }||{\mathbf{\alpha }}_i|{|}_1$$
    固定αi来更新字典B：
    $$mi{n}_{\mathbf{B}}||\mathbf{X}-\mathbf{B}\mathbf{A}|{|}_F^2$$
    重写上式：
    

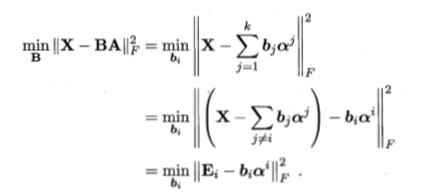
11.6 压缩感知

1、问题：根据部分信息恢复全部信息

• 奈奎斯特(Nyquist)采样定理：令采样频率达到模拟信号最高频率的两倍，则采样后的数字信号就保留了模拟信号的全部信息
• 影响重构原信号的因素
  传递、存储：对采样的数字信号进行压缩，可能损失信息
  信号传输：信道出现丢包等问题，可能损失信息

2、例子：通过稀疏表示求解欠定方程

3、两个阶段

• 感知测量：关注如何对原始信号进行处理以获得稀疏样本表示（傅里叶变换、小波变换…）
• 重构恢复：关注如何基于稀疏性从少量观测中恢复原信号

4、压缩感知相关理论：限定等距性(Restricted Isometry Property, RIP)

压缩感知问题转化为L1范数最小问题求解（如上式可转化为LASSO等价形式->近端梯度下降求解——基寻踪去噪）

5、基于部分信息恢复全部信息技术的应用（协同过滤任务：推荐系统——矩阵补全[低秩矩阵恢复]）
目标函数：$mi{n}_{\mathbf{X}}rank(\mathbf{X})$
限制条件：$s.t.(\mathbf{X}{)}_{ij}=(\mathbf{A}{)}_{ij},(i,j)\in \Omega$
X的核范数（边范数）：$||\mathbf{X}|{|}_{\ast }={\sum }_{j=1}^{min(m,n)}{\sigma }_j(\mathbf{X})$
最小化矩阵核范数求解：$mi{n}_{\mathbf{X}}||\mathbf{X}|{|}_{\ast }$、$s.t.(\mathbf{X}{)}_{ij}=(\mathbf{A}{)}_{ij},(i,j)\in \Omega$
凸优化问题，半正定规划(SDP)求解

这篇关于机器学习理论 | 周志华西瓜书 第十一章：特征选择与稀疏学习的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---