稀疏专题
稀疏自编码器tensorflow
自编码器是一种无监督机器学习算法，通过计算自编码的输出与原输入的误差，不断调节自编码器的参数，最终训练出模型。自编码器可以用于压缩输入信息，提取有用的输入特征。如,[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]四比特信息可以压缩成两位,[0,0],[1,0],[1,1],[0,1]。此时，自编码器的中间层的神经元个数为2。但是，有时中间隐藏层的神经元
【稀疏矩阵】使用torch.sparse模块
文章目录 稀疏矩阵的格式coocsrcsc Construction of Sparse COO tensorsConstruction of CSR tensorsLinear Algebra operations（稀疏与稠密之间混合运算）Tensor methods and sparse（与稀疏有关的tensor成员函数）coo张量可用的tensor成员函数（经实测，csr也有一些可以用
基于深度学习的稀疏感知器设计
基于深度学习的稀疏感知器（Sparse Perceptron）设计旨在构建高效的神经网络结构，通过在网络中引入稀疏性来减少计算和存储需求，同时保持模型的性能。这种设计方法不仅适用于深度感知器（如全连接层），还适用于卷积神经网络（CNN）和图神经网络（GNN）等复杂结构。 1. 稀疏感知器的背景与动机 深度学习模型，尤其是全连接层（如感知器），通常拥有大量的参数和复杂的计算操作，这导致了： 高
Spark中的稀疏矩阵
SparkMLlib中的稀疏矩阵写法是这样的： Matrices.sparse(3,2,Array(0,1,3), Array(0,2,1), Array(9,6,8)) 或者写成这样： Matrices.sparse(3, 2, [0, 1, 3], [0, 2, 1], [9, 6, 8]) 这是一个3×2的即3行2列的矩阵写法 这个东西执行完结果是这样的: (0,0) 9.
CEASC:基于全局上下文增强的自适应稀疏卷积网络在无人机图像上的快速目标检测
Adaptive Sparse Convolutional Networks with Global Context Enhancement for Faster Object Detection on Drone Images 摘要 提出了一种基于稀疏卷积的探测头优化方法，该方法在精度和效率之间取得了较好的平衡。然而，该算法对微小物体的上下文信息融合不足，
2-79 基于matlab的卷积稀疏的形态成分分析的医学图像融合
基于matlab的卷积稀疏的形态成分分析的医学图像融合，基于卷积稀疏性的形态分量分析 (CS-MCA) 的稀疏表示 (SR) 模型，用于像素级医学图像融合。通过 CS-MCA 模型使用预先学习的字典获得其卡通和纹理组件的 CSR。然后，合并所有源图像的稀疏系数，并使用相应的字典重建融合分量。最后，实现融合图像计算。程序已调通，可直接运行。 2-79 卷积稀疏的形态成分分析 - 小红书 (xi
【综述】 从稀疏的数据中进行深度补全：Deep Depth Completion from Extremely Sparse Data: A Survey
【综述】 从稀疏的数据中进行深度补全：Deep Depth Completion from Extremely Sparse Data: A Survey 占坑，3日内更新
稀疏数据的优化之道：PyTorch中torch.sparse的高效应用
稀疏数据的优化之道：PyTorch中torch.sparse的高效应用 在机器学习和数据科学领域，稀疏矩阵是一类特殊而又常见的数据结构，特别是在处理大规模文本数据或社交网络关系时。PyTorch，作为当前深度学习研究和应用的主流框架之一，提供了对稀疏矩阵的原生支持。本文将深入探讨如何在PyTorch中使用torch.sparse模块来高效处理稀疏数据。 1. 稀疏矩阵简介 稀疏矩阵是指大部分
数据结构学习之稀疏数组
稀疏数组应用场景 适用于压缩，对于二维数组冗余数据较多，压缩成稀疏数组 当一个数组的大部分数据为0，或者为同一个数时，可以使用稀疏数组进行压缩 属于非线性结构 步骤 1 定义二维数组 2 转换成稀疏数组 遍历二维数组 得到有效数据个数sum 根据sum创建稀疏数组 讲二维数组有效的数据存入稀疏数组 3 稀疏数组转换成二维数组 读取第一行数据 转换后续数据 代
简单了解B+树和密集、稀疏索引
B+树是B树的变体，定义基本与B树相同，除了： 非叶子节点的子树指针与关键字个数相同；非叶子节点的子树指针P[i]，指向关键字值[K[i], K[i+1])的子树，这里必须是小于K[i+1]的，（也有的说是不一定是大于等于K[i]）；非叶子节点只用来存储索引，叶子节点才是存储数据的；（也就是说所有的节点都是需要从根节点到叶子节点，B+树也会更矮）所有叶子节点均有一个链指针指向下一个叶子节点；（B
机器学习第十一章--特征选择与稀疏学习
一、子集搜索与评价 我们将属性称为 “特征”(feature），对当前学习任务有用的属性称为 “相关特征”(relevant feature）、没什么用的属性称为 “无关特征”(irrelevant feature)．从给定的特征集合中选择出相关特征子集的过程，称为“特征选择”(feature selection). 有两个很重要的原因：减轻维数灾难问题、降低学习任务的难度. “冗余特征”(
「单细胞转录组系列」如何从稀疏矩阵中提取部分数据进行分析
这一篇文章是回答知识星球中一位星友的提问，她的电脑内存有限，无法直接使用所有数据，只能分析部分数据。 数据来源: https://content.cruk.cam.ac.uk/jmlab/atlas_data.tar.gz 解压缩之后，得到下面数据 数据清单 其中raw_counts.mtx是以稀疏矩阵格式存放的表达量数据，文件为6.5G, 用普通的文本编辑器无法打开，
【稀疏三维重建】Flash3D：单张图像重建场景的GaussianSplitting
项目主页：https://www.robots.ox.ac.uk/~vgg/research/flash3d/ 来源：牛津、澳大利亚国立 提示： 文章目录 摘要1.引言2.相关工作3.方法3.1 背景：从单个图像中重建场景3.2 单目 4.实验4.14.2 跨域新视角合成4.3 域内新视图合成4.4 域内新视图合成 摘要 Flash3D，一种通用的单一图像场景重建。
【机器学习】Lasso回归：稀疏建模与特征选择的艺术
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈｜ 炫酷HTML | JavaScript基础 💫个人格言: "如无必要，勿增实体" 文章目录 Lasso回归：稀疏建模与特征选择的艺术引言一、Lasso回归简介1.1 基本概念1.2 数学表达式 二、算法与实现2.1 解决方案2.2 Python实现示例 三、Lasso回归的优势与特性3.1
Python俄罗斯方块可操纵卷积分类 | 稀疏辨识算法 | 微分方程神经求解器
🎯要点 🎯组卷积网络：实现循环组，可视化组动作，实现提升卷积核，MNIST 训练数据集训练组卷积网络的泛化能力 | 🎯可操控卷积网络：紧群的表征与调和分析，代码验证常规表征结果，不可约表征实现，傅里叶变换对群调和分析，实现可操控卷积网络 | 🎯深度概率模型：给定高维和结构化对单变量响应变量建模，实现分类响应模型，顺序响应模型、序列标记模型 | 🎯深度离散潜变量模型：使用FashionM
![[CUDA 学习笔记] 稀疏矩阵向量乘法(SpMV) CUDA 实现与优化](https://img-blog.csdnimg.cn/direct/49e9c610c3d04ee8b27608db0a68f680.png)
[CUDA 学习笔记] 稀疏矩阵向量乘法(SpMV) CUDA 实现与优化
稀疏矩阵向量乘法(SpMV) CUDA 实现与优化 本文主要围绕基于 CUDA 的 SpMV 实现进行介绍, 包括几种典型稀疏矩阵存储格式下 SpMV 的朴素实现, 以及 CSR 格式下的几种优化实现. 稀疏矩阵存储格式 稀疏矩阵即含有大量零元的矩阵. 对于稀疏矩阵, 像稠密矩阵一样使用二维数组来存储数据会浪费大量内存空间, 一般采用特殊的数据结构来存储非零元, 以减少内存使用并尽可能有较高
稀疏矩阵coo_matrix、csr_matrix
coo_matrix 内存占用比csr_matrix少，易手工构建 例如： data即元素，row,col分别是稀疏矩阵中元素的坐标位置 >>> import numpy as np>>> data = np.array([4,5,7,9])>>> dataarray([4, 5, 7, 9])>>> row = np.array([0,3,1,0])>>> rowarray([0
论文阅读（一种新的稀疏PCA求解方式）Sparse PCA: A Geometric Approach
这是一篇来自JMLR的论文，论文主要关注稀疏主成分分析（Sparse PCA）的问题，提出了一种新颖的几何解法（GeoSPCA）。 该方法相比传统稀疏PCA的解法的优点：1）更容易找到全局最优；2）计算效率更高；3）因为不再需要计算存储整个协方差矩阵，所以对存储资源需求更少；4）GeoSPCA能够一次性构建所有主成分，而不是通过迭代的方式逐步添加，这有助于避免因迭代过程中的数据秩减而导致的信息损
稀疏高效扩散模型：推动扩散模型的部署与应用
数据驱动的世界中，生成模型扮演着至关重要的角色，尤其是在需要创建逼真样本的任务中。扩散模型（Diffusion Models, DM），以其卓越的样本质量和广泛的模式覆盖能力，已经成为众多数据生成任务的首选。然而，这些模型在实际部署时面临的挑战，如长时间的推理过程和对内存的大量需求，限制了它们在资源受限的设备上的应用。为了克服这些限制，本文提出了一种创新的稀疏微调方法，旨在不牺牲生成质量的前提下，
C/C++利用三元组实现稀疏矩阵运算
三元组（（x，y），z）其中（x，y）表示非零元位置，z表示该坐标的值 由于实际操作时，我们所用的矩阵0非常多，所以一个一个输入值很浪费时间，也浪费空间，所以用一些三元组表示非零元即能表示一个矩阵 三元组稀疏矩阵表示一些图也是很不错的选择 这样就很浪费空间，三元组直接 ((0,1),1)((1,2),1)((3,4),1)((5,6),1)((7,8),1) 下面是稀疏矩阵代
（2024，ViT，小波变换，图像标记器，稀疏张量）基于小波的 ViT 图像标记器
Wavelet-Based Image Tokenizer for Vision Transformers 公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群） 目录 0 摘要 1 引言 3 基于小波的图像压缩简介 4 图像标记器 4.1 像素空间标记嵌入 4.2 语义标记嵌入 4.3 Transformer 层的操作计数
昆仑万维官宣开源2000亿稀疏大模型Skywork-MoE
6月3日，昆仑万维宣布开源2千亿稀疏大模型Skywork-MoE，性能强劲，同时推理成本更低。 据「TMT星球」了解，Skywork-MoE基于之前昆仑万维开源的Skywork-13B模型中间checkpoint扩展而来，是首个完整将MoE Upcycling技术应用并落地的开源千亿MoE大模型，也是首个支持用单台4090服务器推理的开源千亿MoE大模型。 开源地址： Skywork-M
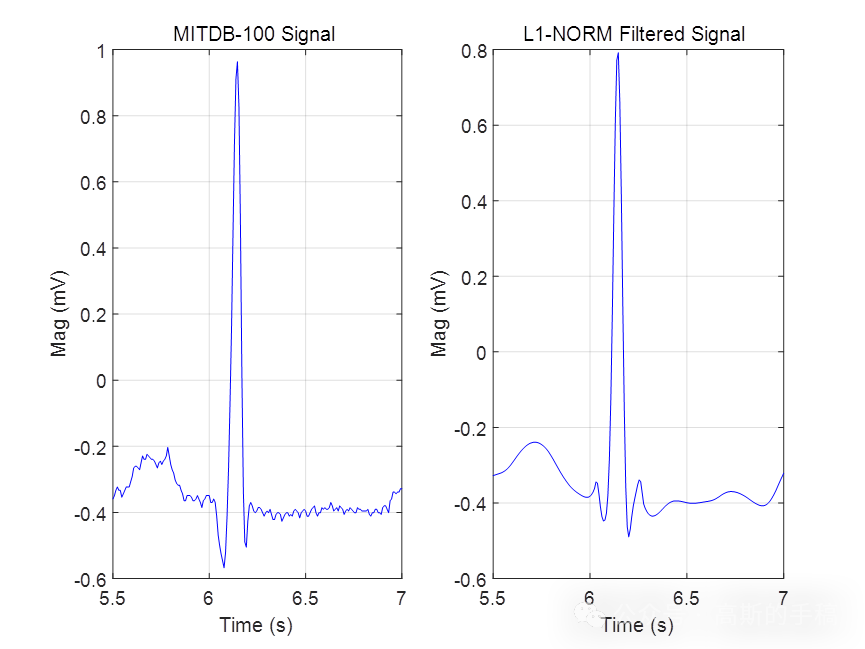
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法（Matlab R2021B）
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量，它的非零系数相对较少，而Tikhonov正则化方法的解通常具有所有的非零系数。即：L2范数正则化方法的解通常是非稀疏的，并且解的结果在一定范围内是发散的，而L1范数正则化方法的解通常是稀疏的。 鉴于此，采用L1范数惩罚的稀疏正则化最小二乘方法对心电信号进行降噪，算法可迁移至金融时间序列，地震信号
matlab——sparse函数和full函数（稀疏矩阵和非稀疏矩阵转换）
函数功能：生成稀疏矩阵 使用方法 ： S = sparse(A) 将矩阵A转化为稀疏矩阵形式，即矩阵A中任何0元素被去除，非零元素及其下标组成矩阵S。 如果A本身是稀疏的，sparse(S)返回S。 S = sparse(i,j,s,m,n,nzmax) 由向量i,j,s生成一个m*n的含有nzmax个非零元素的稀疏矩阵S，并且有 S(i(k),j(k)) = s(k)。 向量 i，j