本文主要是介绍周志华《Machine Learning》学习笔记(6)--神经网络,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上篇主要讨论了决策树算法。首先从决策树的基本概念出发,引出决策树基于树形结构进行决策,进一步介绍了构造决策树的递归流程以及其递归终止条件,在递归的过程中,划分属性的选择起到了关键作用,因此紧接着讨论了三种评估属性划分效果的经典算法,介绍了剪枝策略来解决原生决策树容易产生的过拟合问题,最后简述了属性连续值/缺失值的处理方法。本篇将讨论现阶段十分热门的另一个经典监督学习算法–神经网络(neural network)。
5、神经网络
在机器学习中,神经网络一般指的是“神经网络学习”,是机器学习与神经网络两个学科的交叉部分。所谓神经网络,目前用得最广泛的一个定义是“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应”。
5.1 神经元模型
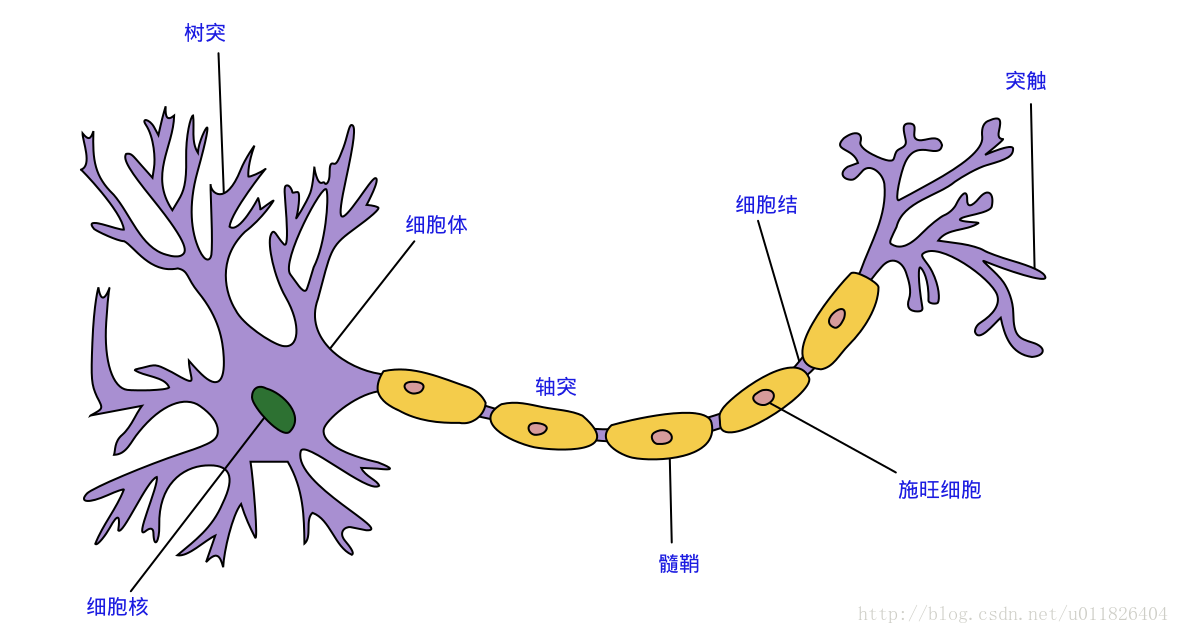
神经网络中最基本的单元是神经元模型(neuron)。在生物神经网络的原始机制中,每个神经元通常都有多个树突(dendrite),一个轴突(axon)和一个细胞体(cell body),树突短而多分支,轴突长而只有一个;在功能上,树突用于传入其它神经元传递的神经冲动,而轴突用于将神经冲动传出到其它神经元,当树突或细胞体传入的神经冲动使得神经元兴奋时,该神经元就会通过轴突向其它神经元传递兴奋。神经元的生物学结构如下图所示,不得不说高中的生化知识大学忘得可是真干净…
一直沿用至今的“M-P神经元模型”正是对这一结构进行了抽象,也称“阈值逻辑单元“,其中树突对应于输入部分,每个神经元收到n个其他神经元传递过来的输入信号,这些信号通过带权重的连接传递给细胞体,这些权重又称为连接权(connection weight)。细胞体分为两部分,前一部分计算总输入值(即输入信号的加权和,或者说累积电平),后一部分先计算总输入值与该神经元阈值的差值,然后通过激活函数(activation function)的处理,产生输出从轴突传送给其它神经元。M-P神经元模型如下图所示:
与线性分类十分相似,神经元模型最理想的激活函数也是阶跃函数,即将神经元输入值与阈值的差值映射为输出值1或0,若差值大于零输出1,对应兴奋;若差值小于零则输出0,对应抑制。但阶跃函数不连续,不光滑,故在M-P神经元模型中,也采用Sigmoid函数来近似, Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内,所以也称为挤压函数(squashing function)。
这篇关于周志华《Machine Learning》学习笔记(6)--神经网络的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!