本文主要是介绍机器学习理论 | 周志华西瓜书 第十六章:强化学习,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第十六章 强化学习
此系列文章旨在提炼周志华《机器学习》的核心要点,不断完善中…
16.1 任务与奖赏
- 通常使用马尔可夫决策过程(MDP)描述
- 目的:找到能长期积累奖赏最大化策略
- 长期奖赏方式
T步积累奖赏: E [ 1 T ∑ t = 1 T r t ] \mathbb{E}[\frac 1 T\sum_{t=1}^Tr_t] E[T1∑t=1Trt]
γ折扣积累奖赏: E [ ∑ t = 0 + ∞ γ t r t + 1 ] \mathbb{E}[\sum_{t=0}^{+∞}\gamma^{t_{r_{t+1}}}] E[∑t=0+∞γtrt+1] - 与监督学习区别:通过尝试发现各个动作结果,没有训练数据告知选择什么动作(某种意义上可看做具有“延迟标记信息”的监督学习问题)
16.2 摇臂赌博机
1、探索与利用
- 两种方法
仅探索法:获知每个摇臂的期望奖赏
仅利用法:执行奖赏最大的动作 - 探索-利用窘境:尝试次数有限
2、ε-贪心
平均奖赏: Q ( k ) = 1 n ∑ i = 1 n v i Q(k)=\frac 1 n\sum_{i=1}^nv_i Q(k)=n1∑i=1nvi
平均奖赏更新: Q n ( k ) = 1 n ( ( n − 1 ) ∗ Q n − 1 ( k ) + v n ) Q_n(k)=\frac 1 n((n-1)*Q_{n-1}(k)+v_n) Qn(k)=n1((n−1)∗Qn−1(k)+vn)
ε-贪心算法描述

3、Softmax
探索和利用进行折中,摇臂概率分配基于Boltzmann分布:

算法描述

16.3 有模型学习(已知模型环境)
1、策略评估:在模型已知时对任意策略能估计出改进策略带来的期望累积奖赏
- 两个函数
- 有状态值函数
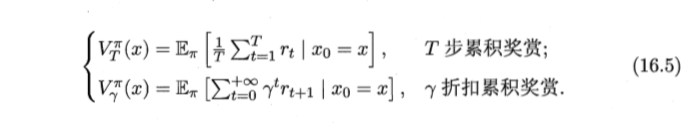
- 状态-动作值函数
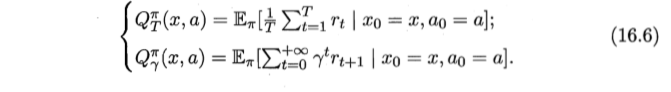
- 有状态值函数
- 值函数的递归形式
- T步奖赏累积

- γ折扣奖赏累积
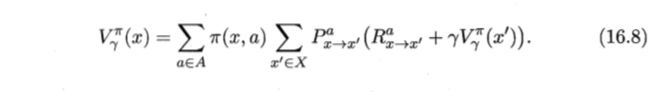
- T步奖赏累积
- 基于T步累积奖赏的策略评估算法

- 结果
状态值函数V→状态动作值函数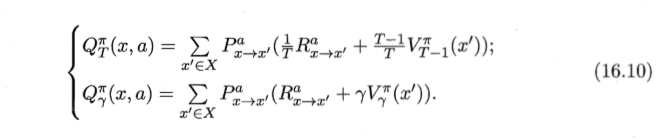
2、策略改进:对某个策略的积累奖赏进行评估后发现非最优,改进
最优状态动作值函数

3、策略迭代与值迭代 - 两种方案
策略迭代:不断迭代进行策略评估和改进知道策略收敛不在改变位置
值迭代:减少耗时 - 两个算法
基于T步累积奖赏的策略迭代算法

基于T步累积奖赏的值迭代算法
16.4 免模型学习(学习算法不依赖环境建模)
1、蒙特卡罗强化学习:通过考虑采样轨迹克服模型位置给策略估计造成的困难
- 同策略蒙特卡罗强化学习算法

- 异策略蒙特卡罗强化学习算法

2、时序差分学习:结合动态规划与蒙特卡罗方法的思想,能做到更高效的免模型学习 - Sarsa算法

- Q-学习算法

16.5 值函数近似
- 概述
值函数:关于有限状态的表格值函数
更改一个状态上的值不会影响其他状态的值 - 线性值函数近似Sarsa算法

16.6 模仿学习(从范例中学习)
- 直接模仿学习:直接模仿人类专家的状态-动作对
- 逆强化学习:从人类专家提供的范例数据中反推出奖赏函数,有助于解决设计奖赏函数困难
迭代式逆强化学习算法
这篇关于机器学习理论 | 周志华西瓜书 第十六章:强化学习的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







