机器学习理论 | 周志华西瓜书 第十二章：计算学习理论

本文主要是介绍机器学习理论 | 周志华西瓜书 第十二章：计算学习理论，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第十二章 计算学习理论

此系列文章旨在提炼周志华《机器学习》的核心要点，不断完善中…

---

12.1 基础知识

1、概述
目的：分析学习任务的困难本质，为学习算法提供理论保证）

2、一些定义

• 令h为从X到Y的映射，h的泛化误差：$E(h;\mathcal{D})=P_{\mathbf{x}\sim \mathcal{D}}(h(\mathbf{x})\ne y)$
• h在D上的经验误差：$\hat{E}(h;D)=\frac{1}{m}{\sum }_{i=1}^m\mathbb{I}(h({\mathbf{x}}_i)\ne y_i)$
• 通过不合(disagreement)度量映射之间差别：$d(h_1,h_2)=P_{\mathbf{x}\sim \mathcal{D}}(h({\mathbf{x}}_1)\ne h({\mathbf{x}}_2))$

3、常用不等式

12.2 PAC学习

1、概述
概率近似正确(Probably Approximately Correct)学习理论

2、一些定义

12.3 有限假设空间

12.3.1 可分情形$(c\in \mathcal{H})$

12.3.2 不可分情形$(c\notin \mathcal{H})$

12.4 VC维

1、几个概念
标记结果的表示： h ∣ D = { ( h ( x 1 ) , h ( x 2 ) , . . . , h ( x m ) ) } h|_D=\{(h(\bm x_1),h(\bm x_2),...,h(\bm x_m))\} h∣D​={(h(x1​),h(x2​),...,h(xm​))}
增长函数(growth function)：

利用增长函数估计经验误差与泛化误差的关系：

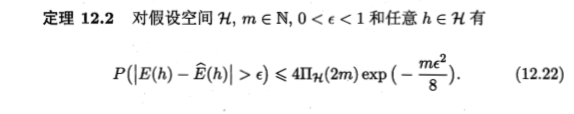
对分(dichotomy)：H中的假设对D中实例赋予标记的每种可能结果称为对D的一种对分
打散(shattering)：假设空间H能实现示例集D上的所有对分

2、VC维的正式定义

VC维与增长函数的密切关系：

由此计算出增长函数的上界：

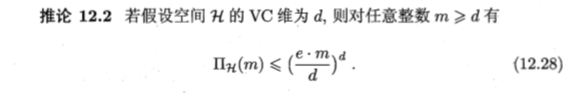
从而得到基于VC维的泛化误差界（分布无关、数据独立的）：

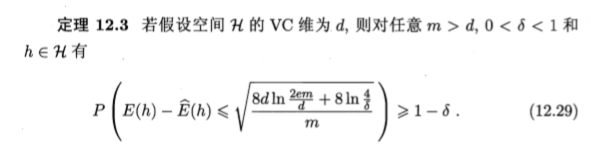
12.5 Rademacher复杂度

1、概述
另一种刻画假设空间复杂度的途径，一定程度考虑数据分布

2、关于函数空间F的泛化误差界

• 定理12.5（回归问题）
  
  
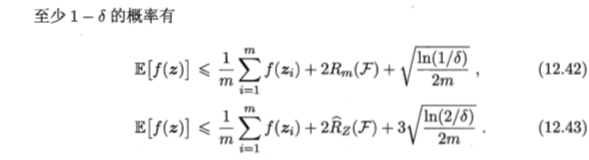
• 定理12.6（二分类问题）
  
• 定理12.7(从Rademacher复杂度和增长函数能推导出基于VC维的泛化误差界)
• 

12.6 稳定性

1、一些定义

• 训练集D的变化
  
• 几种损失
  
  2、算法的均匀稳定性(uniform stability)
  定义12.10（移除示例稳定性包含替换示例稳定性）
  
  定理12.8（给出基于稳定性分析推导出的学习算法学得假设的泛化误差界）
  
  定理12.9 若学习算法 是ERM且稳定的，则假设空间H可学习

这篇关于机器学习理论 | 周志华西瓜书 第十二章：计算学习理论的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---