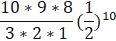二项分布专题
概率论(二)-随机变量及其分布:分布函数F(x)、离散型随机变量【分布律:(0-1)分布、二项分布、泊松分布】、连续型随机变量【概率密度:均匀分布、指数分布、正态/高斯分布】、3σ法则、偏度、峰度
1 随机变量 2 离散型随机变量及其分布律 3 随机变量的分布函数 4 连续型随机变量及其概率密度 5 随机变量的函数的分布
[概率论]-离散型随机变量·二项分布
离散型随机变量 设X是一个随机变量,如果它全部可能的取值只有有限个或可数无穷个,则称X为一个离散型随机变量。 二项分布 伯努利实验 伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努
伯努利试验和二项分布
伯努利试验和二项分布 概念 设试验E只有两个可能结果,A和非A,则称E为伯努利试验,设P(A)=p(0 < p < 1),此时P(非A)=1-p;将E独立重复地进行n次,则称这一串重复的独立试验为n重伯努利试验。 二项分布 在数学中,典型的伯努利试验有,将硬币抛n次,就是n重伯努利试验,抛一个骰子,若A表示得到“1”点,q表示非“A”点,将骰子抛n次,就是n重伯努利试验。 以X表示n重伯
【概率论】5-2:伯努利和二项分布(The Bernoulli and Binomial Distributions)
原文地址1:https://www.face2ai.com/Math-Probability-5-2-the-Bernoulli-and-Binomial-Distributions转载请标明出处 Abstract: 本文介绍Bernoulli Distribution (伯努利分布)和Binomial Distribution(二项分布) Keywords: Bernoulli Distrib
小白入门python如何理解二项分布?
在我们生活中,抛出硬币无非是落下是正面或反面,类似于成功或失败的这样的只有两个可能结果的分布背称为二项分布。二项分布在我们的生活中无所不在,是概率统计中非常基础、非常实用的一种分布,本文介绍python中的二项分布。 1、二项分布是什么? 二项分布(Binomial Distribution)是概率统计中非常基础、非常实用的一种分布。 二项式分布就是只有两个可能结果的分布,比如成功或失败
python统计分析——二项分布
参考资料:用python动手学统计学 广义线性模型的一大特征是可以使用非正态分布。为了能够正确地应用广义线性模型,我们需要知道除了正态分布还有哪些常见的概率分布。 1、导入库 # 导入库# 用于数值计算的库import numpy as npimport pandas as pdimport scipy as spfrom scipy import stats#
假设检验:以样本服从二项分布举例
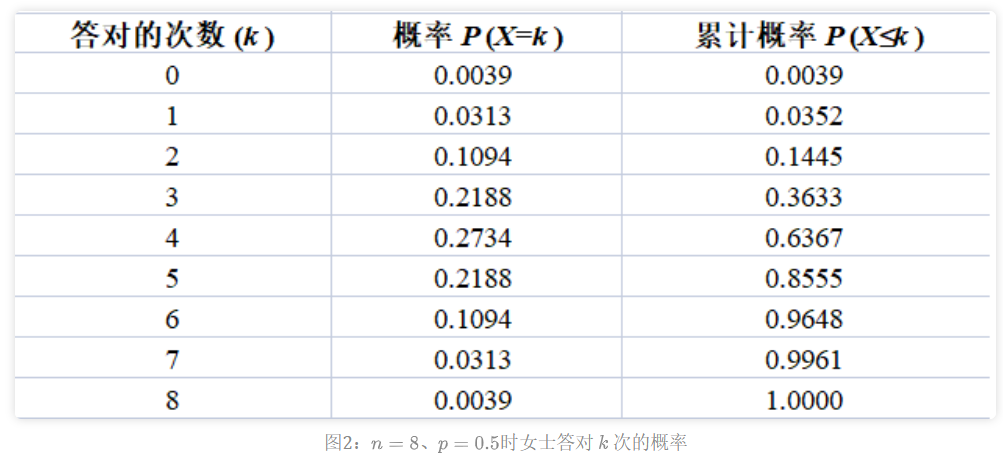
目录 假设检验一、假设检验的思想二、假设检验的基本步骤1. 确定要进行检验的假设2. 选择检验统计量3. 确定用于做决策的拒绝域4. 求出检验统计量的值5. 查看样本结果是否位于拒绝域内6. 做出决策 三、举例说明例子1——某公司治疗打鼾例子2——女士品茶的故事 假设检验 一、假设检验的思想 假设检验的基本思想是 “小概率事件”原理 ,其统计推断方法是带有某种概率性质的反证
人工智能数学基础--概率与统计10:离散随机变量的概率函数及常见的二项分布、泊松分布
一、离散随机变量的概率函数及分布函数 设X为离散随机变量,其全部可能取值为{a1,a2,…},则:pi=P(X=ai) (i=1,2,…)称为X的概率函数,也称为随机变量X的概率分布; 设X为随机变量(包括离散和非离散),则函数:P(X≤x) = F(x) (-∞ < x <∞) 称为X的分布函数; 结合概率函数和分布函数的定义,对于离散随机变量,有: P(i) = P(X=i)
使用R语言计算二项分布的概率和累计概率
需求描述 利用R语言计算二项分布的概率和累计概率。 问题分析 假设某个试验是伯努利试验,其成功概率用p表示,那么失败的概率为q=1-p。进行n次这样的试验,成功了x次,则失败次数为n-x,发生这种情况的概率可用下面公式来计算: 计算过程为: = =120*0.0009765625 =0.1171875 这里的概率称之为概率质量函数,简称概率函数,而R里称之为密度函数是
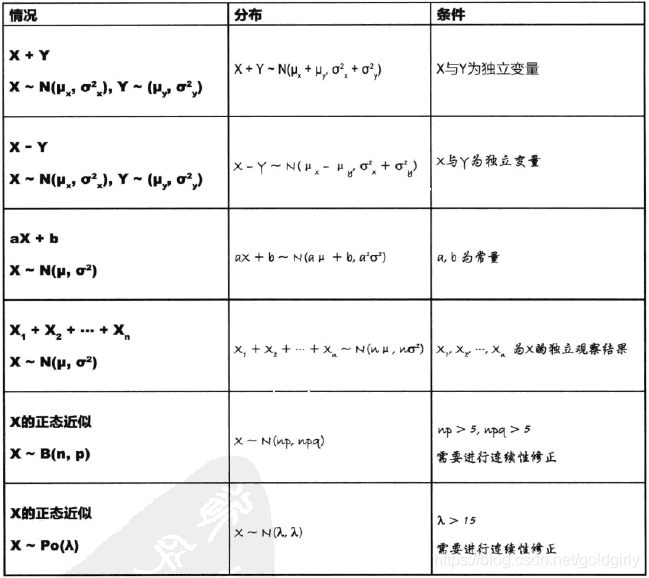
均匀分布二项分布泊松分布正态分布Z=X+Y的概率密度Z=X/YZ=XYmax{X,Y}的分布min{X,Y}的分布
泊松分布 均匀分布 正态分布 Z=X+Y Z=X/Y&&Z=XY max{X,Y}的分布&&min{X,Y}的分布
SPSS二项分布检验
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下载:SPSS数据分析专栏附件! 1.二项分布检验 二项分布检验是一种常见的假设检验方法,适用于一次试验中只有两种可能结果的情况,例如投硬币或抛骰子,或者产品质量检验中有合格
伯努利二项分布的相对高概率与实际的低概率
伯努利二项分布的相对高概率与实际的低概率 计算公式 P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k)=C_{n}^{k} p^k(1-p)^{n-k} P(X=k)=Cnkpk(1−p)n−k n n n 表示试验次数, p p p 表示事件出现的概率, k k k 表示事件出现的次数 简单理解就是,盒子里有total个小球,有 p ∗ t
学习不同概率分布(二项分布、泊松分布等)概念及基础语法
概率分布是描述随机变量取值的概率情况的函数。常见的概率分布包括二项分布、泊松分布等。 二项分布(Binomial Distribution):描述了一次试验中成功事件发生的次数的概率分布。它的基础语法如下: 概率质量函数:pmf(k, n, p) 表示在n次试验中成功k次的概率。累积分布函数:cdf(k, n, p) 表示在n次试验中成功不超过k次的概率。期望:mean(n, p) 表示n次试验
python 二项分布模拟_Python | 二项式实验模拟
python 二项分布模拟 A binomial experiment is described by the following characteristics: 二项式实验由以下特征描述: An experiment that involves repeated trials. 涉及重复试验的实验。 Each trial can only have two possible outcom
统计学2:随机变量分布规律(二项分布、泊松分布、正态分布)
1、离散型随机变量的分布规律:二项分布、泊松分布(Binomial Distribution, Poisson Distribution) -二项分布(Binomial Distribution)泊松分布(Poisson Distribution)怎么计算? X ∼ B ( n , p ) P ( X = k ) = C n k p k q n − k X\sim B\left(n,p\righ
二项分布累积分布函数绘制
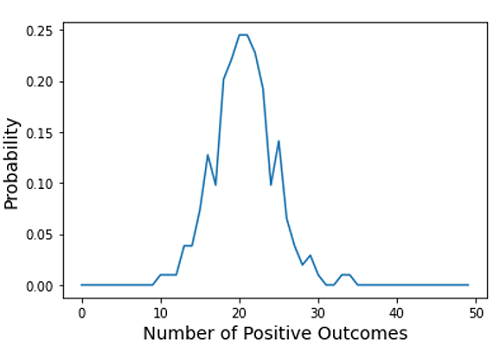
1. 二项分布 2. 示例 投篮n次;投中概率0.1。 import matplotlib.pyplot as pltimport numpy as np from scipy.special import comb, permfrom scipy import integratefig, ax = plt.subplots(1, 1)n = 500p = 0.1res =


![[概率论]-离散型随机变量·二项分布](/front/images/it_default.gif)