本文主要是介绍统计学2:随机变量分布规律(二项分布、泊松分布、正态分布),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、离散型随机变量的分布规律:二项分布、泊松分布(Binomial Distribution, Poisson Distribution)
| - | 二项分布(Binomial Distribution) | 泊松分布(Poisson Distribution) |
|---|---|---|
| 怎么计算? | X ∼ B ( n , p ) P ( X = k ) = C n k p k q n − k X\sim B\left(n,p\right)\ \ \ P\left(X=k\right)=C_n^kp^kq^{n-k} X∼B(n,p) P(X=k)=Cnkpkqn−k | X ∼ B ( λ ) P ( X = k ) = λ k k ! e − λ E ( X ) = V a r ( X ) = λ X\sim B\left(\lambda\right)\ \ \ P\left(X=k\right)=\frac{\lambda^k}{k!}e^{-\lambda}\\E\left(X\right) =Var\left(X\right) =\lambda X∼B(λ) P(X=k)=k!λke−λE(X)=Var(X)=λ |
| 如何判断是否适用? | 1 ) 做 某 件 事 的 次 数 固 定 , 为 n 2 ) 每 件 事 有 两 种 结 果 3 ) 每 次 成 功 的 概 率 相 等 , 为 p 4 ) 在 n 次 试 验 中 , 计 算 成 功 k 次 的 概 率 1) 做某件事的次数固定,为n \\2)每件事有两种结果\\3)每次成功的概率相等,为p\\4)在n次试验中,计算成功k次的概率 1)做某件事的次数固定,为n2)每件事有两种结果3)每次成功的概率相等,为p4)在n次试验中,计算成功k次的概率 | 1 ) 事 件 是 独 立 事 件 2 ) 任 意 相 同 的 时 间 范 围 内 或 任 意 相 同 的 区 域 范 围 内 , 事 件 发 生 的 概 率 相 同 , 为 λ 3 ) 在 某 个 时 间 范 围 内 , 计 算 发 生 某 件 事 k 次 的 概 率 1)事件是独立事件\\2)任意相同的时间范围内或任意相同的区域范围内,事件发生的概率相同,为\lambda\\3)在某个时间范围内,计算发生某件事k次的概率 1)事件是独立事件2)任意相同的时间范围内或任意相同的区域范围内,事件发生的概率相同,为λ3)在某个时间范围内,计算发生某件事k次的概率 |
| 举个栗子 | 1 ) 抛 5 次 硬 币 , 求 2 次 正 面 朝 上 的 概 率 1) 抛5次硬币,求2次正面朝上的概率 1)抛5次硬币,求2次正面朝上的概率 | 1 ) 求 一 个 月 内 某 机 器 损 坏 10 次 的 概 率 2 ) 求 一 个 路 段 一 小 时 内 经 过 9 辆 车 的 概 率 1)求一个月内某机器损坏10次的概率\\2)求一个路段一小时内经过9辆车的概率 1)求一个月内某机器损坏10次的概率2)求一个路段一小时内经过9辆车的概率 |
X:随机变量
期望值和均值
在总体样本量未知时使用期望值计算总体样本均值
二项分布的期望值: E ( x ) = n p E\left(x\right) =np E(x)=np
二项分布
二项式系数公式
( n k ) = C n k = n ! k ! ( n − k ) ! \binom{n}{k}=C^k_n=\frac{n!}{k!\left(n-k\right)!} (kn)=Cnk=k!(n−k)!n!
二项分布与泊松分布
泊松分布公式的推导就是将一段时间范围无限等分,使得每次事件发生都在一个等分的时间范围内,这时这些时间段内发生事件与否就遵循二项分布
泊松分布的推导过程(摘自https://jentchang.github.io/2019/01/01/stats-25/)
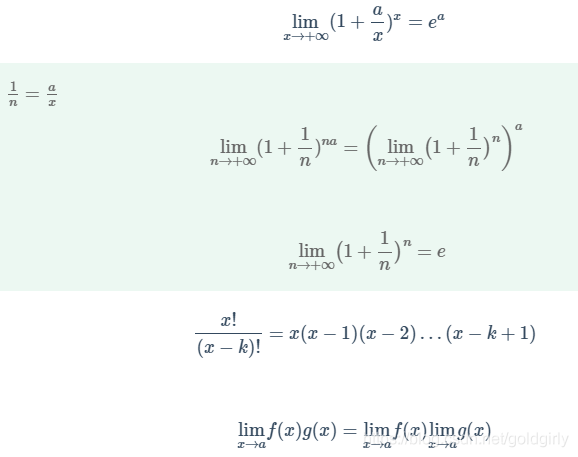

2、连续型随机变量的分布规律:概率密度函数、正态分布(Normal Distribution/ Gaussian Distribution/Bell Curve)
1)正态分布密度函数
X ∼ N ( μ , σ 2 ) P ( X ) = 1 σ 2 π e − 1 2 ( x − μ σ ) 2 X\sim N\left({\mu,\sigma^2}\right)\ \ \ P\left(X\right)=\frac{1}{\sigma\sqrt{2\pi}}^{e^{-\frac{1}{2}}\left(\frac{x-\mu}{\sigma}\right)^2} X∼N(μ,σ2) P(X)=σ2π1e−21(σx−μ)2
其中标准z分数: z = x − μ σ z=\frac{x-\mu}{\sigma} z=σx−μ
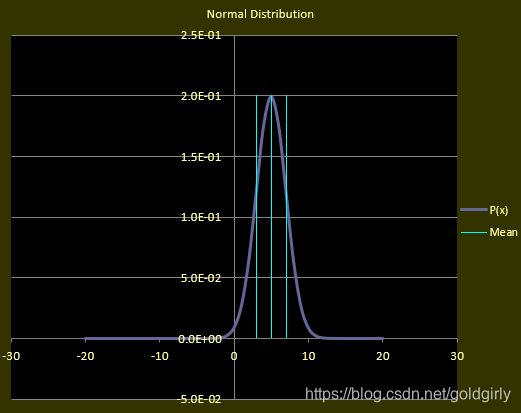
X ∼ N ( 0 , 1 ) X\sim N\left({0,1}\right) X∼N(0,1)为标准正态分布
在概率密度函数的图像中,纵轴为概率密度,概率是对应的面积
2)正态分布密度函数的特点
- 均值μ为对称轴。
- 标准差σ表示图形的宽窄,标准差越小,数值越向平均值靠拢(可以理解为标准差是到均值的平均距离)
- 二项分布是有限的,正态分布在整个实轴上都有定义,即概率密度不会等于0。(尽管延伸出去概率极小,但也是存在的)
3)经验法则
P ( μ − σ < X < μ + σ ) = 68 % P\left(\mu-\sigma<X<\mu+\sigma\right)=68\% P(μ−σ<X<μ+σ)=68%
P ( μ − 2 σ < X < μ + 2 σ ) = 95 % P\left(\mu-2\sigma<X<\mu+2\sigma\right)=95\% P(μ−2σ<X<μ+2σ)=95%
P ( μ − 3 σ < X < μ + 3 σ ) = 99.7 % P\left(\mu-3\sigma<X<\mu+3\sigma\right)=99.7\% P(μ−3σ<X<μ+3σ)=99.7%

4)正态分布的近似
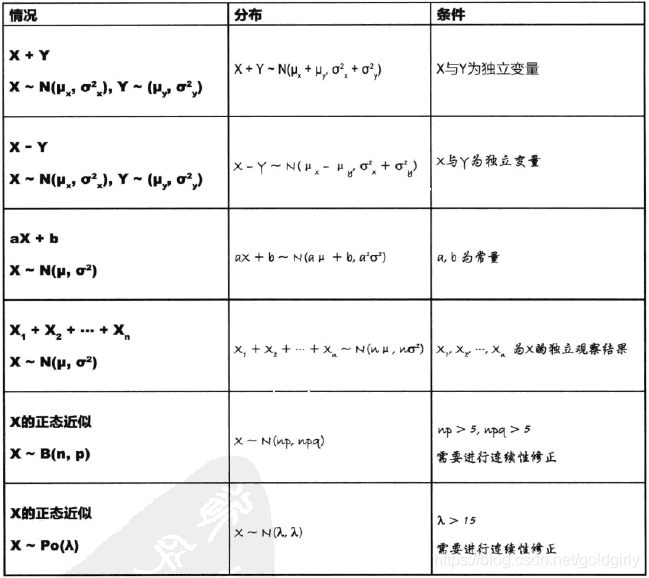
3、 python实现正态分布(待补充)
参考资料:
可汗学院统计学:https://www.bilibili.com/video/av7199273/?p=73
简客:https://jentchang.github.io/contents/math/statistical.html
《深入浅出统计学》
这篇关于统计学2:随机变量分布规律(二项分布、泊松分布、正态分布)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






