本文主要是介绍python统计分析——二项分布,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考资料:用python动手学统计学
广义线性模型的一大特征是可以使用非正态分布。为了能够正确地应用广义线性模型,我们需要知道除了正态分布还有哪些常见的概率分布。
1、导入库
# 导入库
# 用于数值计算的库
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats
# 用于绘图的库
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()2、二项分布
设成功的概率为p,进行N次独立的伯努利试验,成功的次数m所服从的离散型概率分布叫作二项分布。二项分布的参数是成功的概率p和试验次数N。
服从二项分布的随机变量m的期望为Np,方差为Np(1-p)
python的二项分布实现如下:
2.1 概率质量函数
# 二项分布的概率质量函数
# k表示成功的次数,n表示试验的次数,p表示成功的概率
sp.stats.binom.pmf(k=1,n=2,p=0.5)
2.2 生成二项分布随机数
# 生成二项分布随机数
# n表示一组试验中的总次数,p表示单次成功的概率,size表示重复次数
sp.stats.binom.rvs(n=10,p=0.2,size=5)
上图结果表示:进行了5组试验,每组试验的次数是10次;第一组试验成功了2次,第二组试验成功了1次,第三组试验成功了5次......
2.3 二项分布图像展示
# 设置N=10,p=0.2的二项分布
binomial=sp.stats.binom(n=10,p=0.2)
# 设置随机种子,用于复现结果
np.random.seed(1)
# 重复试验1000次
rvs_binomial=binomial.rvs(size=10000)
# 概率质量函数
m=np.arange(0,10,1)
pmf_binomial=binomial.pmf(k=m)
# 绘制样本直方图与概率质量函数的图形
sns.histplot(rvs_binomial,bins=m,stat='density')
plt.plot(m,pmf_binomial)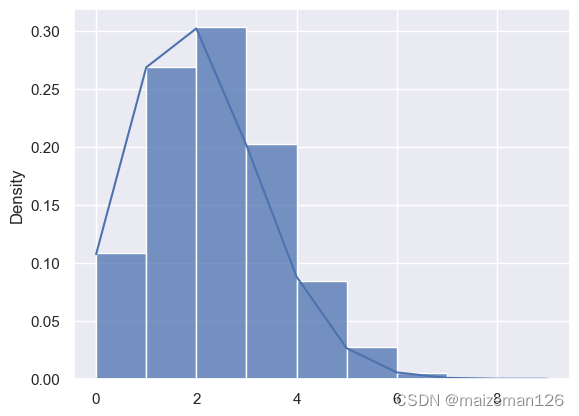
这篇关于python统计分析——二项分布的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




