python 二项分布模拟_Python | 二项式实验模拟

python 二项分布模拟

A binomial experiment is described by the following characteristics:

二项式实验由以下特征描述：

• An experiment that involves repeated trials.

  涉及重复试验的实验。

• Each trial can only have two possible outcomes i.e. success or failure.

  每个试验只能有两个可能的结果，即成功或失败。

• The likelihood of a particular outcome will occur on any given trial that remains constant throughout the experiment.

  在整个实验过程中保持不变的任何给定试验中，都会出现特定结果的可能性。

• All of the trials are independent of the experiment.

  所有试验均独立于试验。

An experiment of a series of coin tosses is a perfect example of a binomial experiment. In this article, we are going to simulate a binomial experiment using an inbuilt function numpy.random.binomial(). This NumPy library function returns a vector containing the number of positive outcomes in n number of trials.

一系列抛硬币实验是二项式实验的完美示例。 在本文中，我们将使用内置函数numpy.random.binomial()模拟一个二项式实验。 此NumPy库函数返回一个向量，其中包含n个试验中的阳性结果数。

Probability of positive outcome: 0.2

阳性结果的可能性：0.2

Following is the python code for demonstration and plotting Probability Distribution of Simulation Binomial Process:

以下是用于演示和绘制模拟二项式过程的概率分布的python代码：

import numpy as np
import matplotlib.pyplot as plt 
n = 100
p = 0.2
x = np.random.binomial(n,p,size = 19)
kk = 0
kr = []
l = 0
for i in range(50):
n = 100
kk = 0
for h in range(100):
# j.append(np.random.binomial(i,p))
jj = np.random.binomial(n,p)
if jj >= i:
kk = kk + 1
kr.append(kk*(100-kk)/10000)                            
# it is number of head
# find the probability of number of head
print(kr)
plt.plot(kr)
plt.xlabel('Number of Positive Outcomes',fontsize=14)
plt.ylabel('Probability',fontsize=14)

Output:

输出：

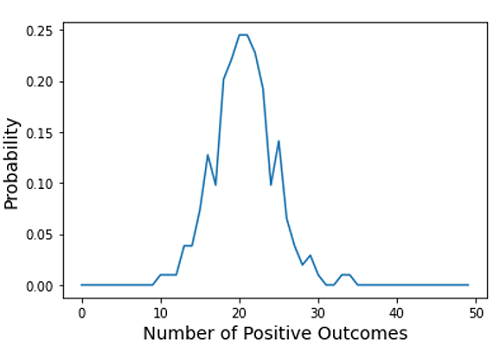
翻译自: https://www.includehelp.com/python/binomial-experiment-simulation.aspx

python 二项分布模拟