二项式专题

量化交易面试：什么是二项式模型？

二项式模型是一种用于描述具有两个可能结果的随机过程的统计模型。它在金融领域特别是在量化交易中有多种应用，比如股票价格变动、期权定价等。以下是对二项式模型的详细解释：基本概念：二项式模型基于二项分布，即每次实验只有两个可能的结果：成功（通常记为1）或失败（通常记为0）。在金融中，这通常用于模型化资产价格在特定时间内的涨跌。二项式树：在量化交易中，二项式模型通常以二项式树的形式表示。在

蓝桥杯算法训练 6-1 递归求二项式系数值

题目：问题描述样例输入一个满足题目要求的输入范例。 3 10 样例输出与上面的样例输入对应的输出。数据规模和约定　　输入数据中每一个数的范围。　　例：结果在int表示时不会溢出。思路：这道题的题目已经给出了解决的方法：递归。剩下的，我的第一反应就是打表，因为题目中给出的数据范围是不会超出整型，所以直接暴力打表。代码如下： #include<stdi

杨辉三角，二项式系数，组合数，斐波那契数列

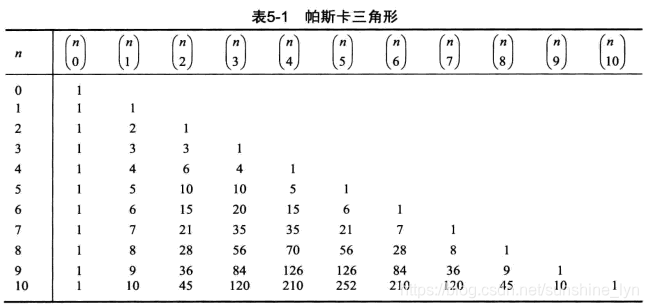
古人就是厉害，在此%杨辉大佬，这个杨辉三角真的是好厉害啊。杨辉三角杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。排列信息: 杨辉三角有多种重要的性质。概述：前提：每行端点与结尾的数为1. 每个数等于它上方两数之和。

CNN中的伯努利分布与二项式分布

伯努利分布是什么？伯努利分布是二项分布的一种特殊情况。在伯努利试验中，只有两个可能的结果，通常用1和0表示，例如成功和失败、正面和反面等。伯努利分布描述了在单次伯努利试验中发生成功的概率。它的概率质量函数为： P(X=k) = p^k * (1-p)^(1-k) 其中，p为成功的概率，k为观察到的结果（成功为1，失败为0）。伯努利分布的期望值为p，方差为p(1-p)。它适用于一些简单的二

package com.supermars.practice;import java.util.Scanner;public class 杨辉三角形与二项式定理递推 {static Scanner cin = new Scanner(System.in);static int C[][] = new int[1 << 7][1 << 7];public static void main(Strin

具体数学之二项式系数2

又是一大堆公式来袭~~ 二项级数的部分和另一种有意思的关系式子： ∑ k ⩽ m ( m + r k ) x k y m − k = ∑ k ≤ m ( − r k ) ( − x ) k ( x + y ) m − k , m 是整数 \sum_{k \leqslant m} \left( \begin{array}{c}{m+r} \\ {k}\end{array}\right)

具体数学之二项式系数1

本章讲述的是二项式系数，包含了一大堆记不住的公式@<@ 1. ( r k ) = { r ( r − 1 ) ⋯ ( r − k + 1 ) k ( k − 1 ) ⋯ ( 1 ) = r k k ! , k ⩾ 0 0 , k < 0 \left( \begin{array}{l}{r} \\ {k}\end{array}\right)=\left\{\begin{array}{l

如何深刻理解从二项式分布到泊松分布

泊松镇贴二项分布和泊松分布的表达式二项分布： P ( x = k ) = C n k p k ( 1 − p ) n − k P(x=k) = C_n^kp^k(1-p)^{n-k} P(x=k)=Cnkpk(1−p)n−k 泊松分布： P ( x = k ) = λ k k ! e − λ P(x=k) = \frac{\lambda^k}{k!}e^{-\lambda} P(

牛顿的广义二项式定理---微积分推倒的开始

Theorem Let α∈R be a real number. Let x∈R be a real number such that |x|<1 . Then: (1+x)α=∑n=0∞αn−n!xn=∑n=0∞1n!(∏k=0n−1(α−k))xn where αn− denotes the falling factorial. That i

python 二项分布模拟_Python | 二项式实验模拟

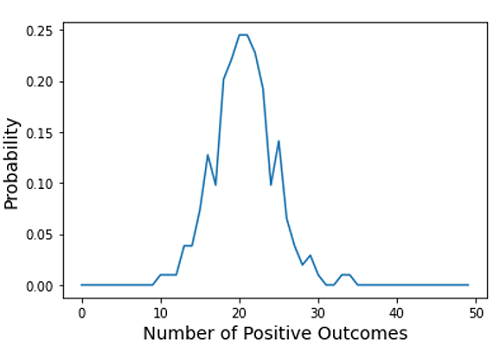
python 二项分布模拟 A binomial experiment is described by the following characteristics: 二项式实验由以下特征描述： An experiment that involves repeated trials. 涉及重复试验的实验。 Each trial can only have two possible outcom

【二进制】【二项式定理】【组合数】C. Moamen and XOR

相同知识点的题目 https://blog.csdn.net/qq_50285142/article/details/122792736 前置知识二项式系数之和： C n 0 + C n 1 + C n 2 + C n 3 + . . . + C n n − 1 + C n n = 2 n C_n^0+C_n^1+C_n^2+C_n^3+...+C_n^{n-1}+C_n^n=2^n Cn

动态规划计算二项式系数

动态规划计算二项式系数，主要用到了一个性质C（m，n）=C（m，n-1）+C(m-1，n-1)；这个式子将C(m , n)的计算问题表述为了（问题描述）C(m-1 , n -1)和C(m -1,n)两个较小的交叠子问题。初始条件：C(m , m) = C(n , 0) = 1 得到c（n,k）: ：代码1（c（n，k）:k为固定值）： [java] vie