本文主要是介绍具体数学之二项式系数1,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本章讲述的是二项式系数,包含了一大堆记不住的公式@<@
1. ( r k ) = { r ( r − 1 ) ⋯ ( r − k + 1 ) k ( k − 1 ) ⋯ ( 1 ) = r k k ! , k ⩾ 0 0 , k < 0 \left( \begin{array}{l}{r} \\ {k}\end{array}\right)=\left\{\begin{array}{l}{\frac{r(r-1) \cdots(r-k+1)}{k(k-1) \cdots(1)}=\frac{r^{k}}{k ! } , k \geqslant 0} \\ {0}, k<0\end{array}\right. (rk)={k(k−1)⋯(1)r(r−1)⋯(r−k+1)=k!rk,k⩾00,k<0
当k=0时,上述结果为1
r为上指标,k为下指标,表示从r个数里面取k个的排序
2.帕斯卡三角形(杨辉三角形)
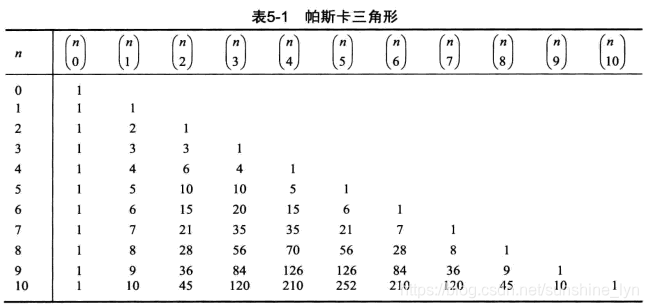
( r 0 ) = 1 , ( r 1 ) = r , ( r 2 ) = r ( r − 1 ) 2 \left( \begin{array}{l}{r} \\ {0}\end{array}\right)=1, \left( \begin{array}{l}{r} \\ {1}\end{array}\right)=r, \left( \begin{array}{l}{r} \\ {2}\end{array}\right)=\frac{r(r-1)}{2} (r0)=1,(r1)=r,(r2)=2r(r−1)
☆ 考虑式子 ( − 1 k ) = ? ( − 1 − 1 − k ) \left( \begin{array}{c}{-1} \\ {k}\end{array}\right) \stackrel{?}{=} \left( \begin{array}{c}{-1} \\ {-1-k}\end{array}\right) (−1k)=?(−1−1−k)
( − 1 k ) = ( − 1 ) ( − 2 ) ⋯ ( − k ) k ! = ( − 1 ) k \left( \begin{array}{c}{-1} \\ {k}\end{array}\right)=\frac{(-1)(-2) \cdots(-k)}{k !}=(-1)^{k} (−1k)=k!(−1)(−2)⋯(−k)=(−1)k
( − 1 − 1 − k ) = ( − 1 ) − 1 − k \left( \begin{array}{c}{-1} \\ {-1-k}\end{array}\right)=(-1)^{-1-k} (−1−1−k)=(−1)−1−k(由上式可以得出),它是1或者-1
因此上述等式总是相等是错误的!
3.吸收等式(5.5)
( r k ) = r k ( r − 1 k − 1 ) \left( \begin{array}{l}{r} \\ {k}\end{array}\right)=\frac{r}{k} \left( \begin{array}{l}{r-1} \\ {k-1}\end{array}\right) (rk)=kr(r−1k−1), 整 数 k ≠ 0 整数 k \neq 0 整数k̸=0
4.相伴恒等式(5.7)
( r − k ) ( r k ) = r ( r − 1 k ) (r-k) \left( \begin{array}{l}{r} \\ {k}\end{array}\right)=r \left( \begin{array}{c}{r-1} \\ {k}\end{array}\right) (r−k)(rk)=r(r−1k)
( r − k ) ( r k ) = ( r − k ) ( r r − k ) , 对 称 性 = r ( r − 1 r − k − 1 ) , 吸 收 等 式 = r ( r − 1 k ) , 对 称 性 \begin{aligned}(r-k) \left( \begin{array}{c}{r} \\ {k}\end{array}\right) &=(r-k) \left( \begin{array}{c}{r} \\ {r-k}\end{array}\right) ,对称性\\ &=r \left( \begin{array}{c}{r-1} \\ {r-k-1}\end{array}\right),吸收等式 \\ &=r \left( \begin{array}{c}{r-1} \\ {k}\end{array}\right) ,对称性\end{aligned} (r−k)(rk)=(r−k)(rr−k),对称性=r(r−1r−k−1),吸收等式=r(r−1k),对称性
5.加法公式(杨辉三角的性质)(5.8)
( r k ) = ( r − 1 k ) + ( r − 1 k − 1 ) \left( \begin{array}{l}{r} \\ {k}\end{array}\right)=\left( \begin{array}{c}{r-1} \\ {k}\end{array}\right)+\left( \begin{array}{l}{r-1} \\ {k-1}\end{array}\right) (rk)=(r−1k)+(r−1k−1),k是整数
利用定义证明:
∑ k ⩽ n ( r + k k ) = ( r 0 ) + ( r + 1 1 ) + ⋯ + ( r + n n ) \sum_{k \leqslant n} \left( \begin{array}{c}{r+k} \\ {k}\end{array}\right)=\left( \begin{array}{l}{r} \\ {0}\end{array}\right)+\left( \begin{array}{c}{r+1} \\ {1}\end{array}\right)+\cdots+\left( \begin{array}{c}{r+n} \\ {n}\end{array}\right) ∑k⩽n(r+kk)=(r0)+(r+11)+⋯+(r+nn) = ( r + n + 1 n ) =\left( \begin{array}{c}{r+n+1} \\ {n}\end{array}\right) =(r+n+1n),n是整数
6.关于上指标求和
∑ 0 ⩽ k ⩽ n ( k m ) = ( 0 m ) + ( 1 m ) + ⋯ + ( n m ) \sum_{0 \leqslant k \leqslant n} \left( \begin{array}{l}{k} \\ {m}\end{array}\right)=\left( \begin{array}{l}{0} \\ {m}\end{array}\right)+\left( \begin{array}{l}{1} \\ {m}\end{array}\right)+\cdots+\left( \begin{array}{l}{n} \\ {m}\end{array}\right) ∑0⩽k⩽n(km)=(0m)+(1m)+⋯+(nm) = ( n + 1 m + 1 ) =\left( \begin{array}{l}{n+1} \\ {m+1}\end{array}\right) =(n+1m+1),整数 m , n ⩾ 0 m, n \geqslant 0 m,n⩾0
∑ k ≤ n ( m + k k ) = ∑ − m ≤ k ⩽ n ( m + k k ) = ∑ − m ≤ k ⩽ n ( m + k m ) = ∑ 0 ⩽ k ⩽ m + n ( k m ) = ( m + n + 1 m + 1 ) = ( m + n + 1 n ) \begin{aligned} \sum_{k \leq n} \left( \begin{array}{c}{m+k} \\ {k}\end{array}\right) &=\sum_{-m \leq k \leqslant n} \left( \begin{array}{c}{m+k} \\ {k}\end{array}\right) \\ &=\sum_{-m \leq k \leqslant n} \left( \begin{array}{c}{m+k} \\ {m}\end{array}\right) \\ &=\sum_{0 \leqslant k \leqslant m+n} \left( \begin{array}{c}{k} \\ {m}\end{array}\right) \\ &=\left( \begin{array}{c}{m+n+1} \\ {m+1}\end{array}\right)=\left( \begin{array}{c}{m+n+1} \\ {n}\end{array}\right) \end{aligned} k≤n∑(m+kk)=−m≤k⩽n∑(m+kk)=−m≤k⩽n∑(m+km)=0⩽k⩽m+n∑(km)=(m+n+1m+1)=(m+n+1n)
7.上指标反转(5.14)
( r k ) = ( − 1 ) k ( k − r − 1 k ) \left( \begin{array}{l}{r} \\ {k}\end{array}\right)=(-1)^{k} \left( \begin{array}{c}{k-r-1} \\ {k}\end{array}\right) (rk)=(−1)k(k−r−1k),k是整数
8. ( − 1 ) m ( − n − 1 m ) = ( − 1 ) n ( − m − 1 n ) (-1)^{m} \left( \begin{array}{c}{-n-1} \\ {m}\end{array}\right)=(-1)^{n} \left( \begin{array}{c}{-m-1} \\ {n}\end{array}\right) (−1)m(−n−1m)=(−1)n(−m−1n) = ( m + n n ) =\left( \begin{array}{c}{m+n} \\ {n}\end{array}\right) =(m+nn),整数 m , n ⩾ 0 m, n \geqslant 0 m,n⩾0
利用上指标公式,也可以推导出下列式子(帕斯卡三角形一行的部分交替求和):
∑ k ≤ m ( r k ) ( − 1 ) k = ( r 0 ) − ( r 1 ) + ⋯ + ( − 1 ) m ( r m ) \sum_{k≤m} \left( \begin{array}{l}{r} \\ {k}\end{array}\right)(-1)^{k}=\left( \begin{array}{l}{r} \\ {0}\end{array}\right)-\left( \begin{array}{l}{r} \\ {1}\end{array}\right)+\cdots+(-1)^{m} \left( \begin{array}{l}{r} \\ {m}\end{array}\right) ∑k≤m(rk)(−1)k=(r0)−(r1)+⋯+(−1)m(rm) = ( − 1 ) m ( r − 1 m ) , m 是 整 数 =(-1)^{m} \left( \begin{array}{c}{r-1} \\ {m}\end{array}\right), \quad m是整数 =(−1)m(r−1m),m是整数
∑ k ⩽ m ( r k ) ( − 1 ) k = ∑ k ⩽ m ( k − r − 1 k ) = ( − r + m m ) = ( − 1 ) m ( r − 1 m ) \begin{aligned} \sum_{k \leqslant m} \left( \begin{array}{c}{r} \\ {k}\end{array}\right)(-1)^{k}=\sum_{k \leqslant m} \left( \begin{array}{c}{k-r-1} \\ {k}\end{array}\right) \\ =\left( \begin{array}{c}{-r+m} \\ {m}\end{array}\right) \\=(-1)^{m} \left( \begin{array}{c}{r-1} \\ {m}\end{array}\right) \end{aligned} k⩽m∑(rk)(−1)k=k⩽m∑(k−r−1k)=(−r+mm)=(−1)m(r−1m)
这篇关于具体数学之二项式系数1的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



