二叉专题
浙大数据结构:04-树7 二叉搜索树的操作集
这道题答案都在PPT上,所以先学会再写的话并不难。 1、BinTree Insert( BinTree BST, ElementType X ) 递归实现,小就进左子树,大就进右子树。 为空就新建结点插入。 BinTree Insert( BinTree BST, ElementType X ){if(!BST){BST=(BinTree)malloc(sizeof(struct TNo
二叉树 - 二叉搜索树中的搜索
700. 二叉搜索树中的搜索 递归: /*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)*
深入理解二叉搜索树(BST)
一棵二叉搜索树(BST)是以一棵二叉树来组织的,可以用链表数据结构来表示,其中,每一个结点就是一个对象,一般地,包含数据内容key和指向孩子(也可能是父母)的指针属性。如果某个孩子结点不存在,其指针属性值为空(NIL)。 二叉搜索树中的关键字key的存储方式总是满足二叉搜索树的性质: 设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点,那么会有y.key<=x.key;如果y是x右子树
二叉搜索树、平衡二叉树、B树、B+树、B*树
二叉查找树 二叉查找树,由于不平衡,如果连续插入的数据是有顺序的、会导致如下图B的所示,此时搜索会退化到O(N) 二叉查找树,也称二叉搜索树,或二叉排序树。其定义也比较简单,要么是一颗空树,要么就是具有如下性质的二叉树: (1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值; (2) 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值; (3) 任
力扣96-不同的二叉搜索树(Java详细题解)
题目链接:96. 不同的二叉搜索树 - 力扣(LeetCode) 前情提要: 因为本人最近都来刷dp类的题目所以该题就默认用dp方法来做。 dp五部曲。 1.确定dp数组和i下标的含义。 2.确定递推公式。 3.dp初始化。 4.确定dp的遍历顺序。 5.如果没有ac打印dp数组 利于debug。 每一个dp题目如果都用这五步分析清楚,那么这道题就能解出来了。 题目思路: 该
C++笔记17•数据结构:二叉搜索树(K模型/KV模型实现)•
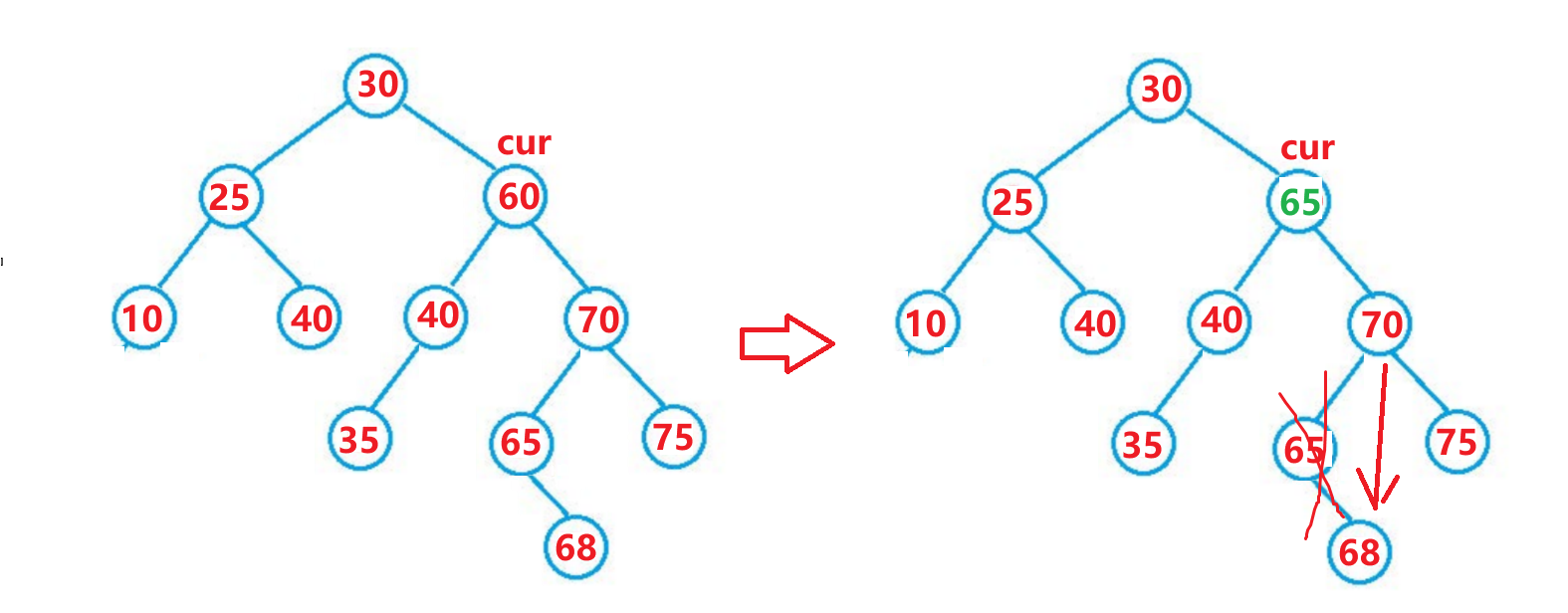
二叉搜索树 1.二叉搜索树 1. 二叉搜索树的查找 a 、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。 b 、最多查找高度次,走到到空,还没找到,这个值不存在。2. 二叉搜索树的插入 插入的具体过程如下: a. 树为空,则直接新增节点,赋值给 root 指针 b. 树不空,按二叉搜索树性质查找插入位置,插入新节点3.二叉搜索树的删除 首先查找元素是否在二叉搜索树中,如果不
【数据结构】详解二叉搜索树及其实现
前言: 二叉搜索树是红黑树等的前身,掌握其操作和性质很重要。总结自用and分享。 目录 一、基本概念 二、其常见操作及其实现 1.定义节点 2.查找元素 3.插入元素 4.删除元素【难点】 三、性质分析 一、基本概念 如下所示:对于所有节点都满足该性质:子树上所有节点的值都小于该节点的值。对于每个节点,右子树上所有节点的值都大于该节点
二叉搜索树(篇1)判断数组是不是二叉搜索树后序遍历的结果
二叉搜索树(Binary Search Tree), 它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。 上图中的二叉搜索树的后序遍历在数组中是:2 9 5 15 16 17 19 18 12 思路: 数组中的最后一个节点是
530. 二叉搜索树的最小绝对差 + 783. 二叉搜索树节点最小距离
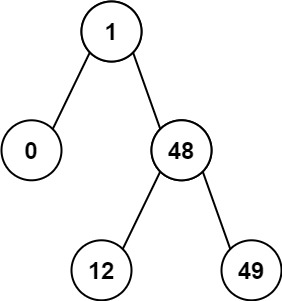
530. 二叉搜索树的最小绝对差 + 783. 二叉搜索树节点最小距离 原题 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其数值等于两值之差的绝对值。 示例 1: 输入:root = [4,2,6,1,3]输出:1 示例 2: 输入:root = [1,0,48,null,null,12,49]输出:1 提示:
【数据结构】二叉搜索树的功能实现详解
文章目录 二叉搜索树查找插入删除找到要删除的节点删除节点1. 要删除节点的左孩子为空2. 要删除节点的右孩子为空3. 要删除的节点的左右孩子都不为空 完整代码 二叉搜索树 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分
LeetCode 重构二叉搜索数,即找出两个被交换的节点
原题:Two elements of a binary search tree (BST) are swapped by mistake. Recover the tree without changing its structure. Note: A solution using O(n) space is pretty straight forward. Could you de
二叉搜索树中的第K大的节点 java实现
题目描述 给定一颗二叉搜索树,请找出其中的第k大的结点。例如, 5 / \ 3 7 /\ /\ 2 4 6 8 中,按结点数值大小顺序第三个结点的值为4。 解题思路:因为这是一颗二叉搜索树,返回的第K个节点其实就是二叉树按中序遍历的第K个节点。 思路一:按中序遍历顺序,将节点一个一个存在LinkedList中,存完之后,取出第k个节点就行啦,这个方法有点low啦 思路二:仍然是按中序遍历,不
【二叉搜索树】K型与KV型二叉搜索树简单实现
关于我: 睡觉待开机:个人主页 个人专栏: 《优选算法》《C语言》《CPP》 生活的理想,就是为了理想的生活! 作者留言 PDF版免费提供:倘若有需要,想拿我写的博客进行学习和交流,可以私信我将免费提供PDF版。 留下你的建议:倘若你发现本文中的内容和配图有任何错误或改进建议,请直接评论或者私信。 倡导提问与交流:关于本文任何不明之处,请及时评论和私信,看到即回
【408DS算法题】033基础-判断二叉树是否是二叉排序树
Index 题目分析实现总结 题目 给定二叉树的根节点root,判断该二叉树是否是二叉排序树。 分析实现 二叉排序树(BST/二叉搜索树):对于每个节点,其左子树中所有节点的值都小于当前结点的值,其右子树中所有节点的值都大于当前结点的值;左子树和右子树本身也是二叉搜索树。 在二叉排序树的定义中含有着递归的思想 - “左子树和右子树本身也是二叉搜索树”,因此可以使用递
leetcode 99:恢复二叉搜索树
方法一:首先使用中序遍历将所有的节点和节点的值存起来,如果是搜索二叉树节点值的数组应该是升序的,找到不是升序的点,交换节点的值,空间复杂度为O(n) void inorder(TreeNode*root,std::vector<TreeNode*>&list,std::vector<int> &vals){if(root==NULL)return;inorder(root->left,l
leetcode 109:有序链表转换二叉搜索树
使用的是递归的方式,所以时间复杂度有些高,48ms TreeNode*newTree(std::vector<int> a,int s,int t){TreeNode*root=NULL;if(t-s==2){root=new TreeNode(a[s+1]);root->left=new TreeNode(a[s]);root->right=new TreeNode(a[s+2]);}el
c-数据结构(二叉搜索树)
树 概念 一组数据中除第一个节点(第一个节点称为根节 点,没有直接前驱节点)之外,其余任意节点有且仅有一个直接前驱,有零个或多个直接后继,这样的一组数据形成一棵树。即用于描述具有层次关系,类似组织架 构关系的一种数据结构。 树的组成:根、分支、叶子 基本术语 节点:树中的元素及其子树 根:树的第一个节点,没有前驱 父节点(parent):某节点的直接前驱就是该节点的父节点 子
[M二叉树] lc236. 二叉树的最近公共祖先(dfs+二叉搜索树)
文章目录 1. 题目来源2. 题目解析 1. 题目来源 链接:236. 二叉树的最近公共祖先 相似题: [M二叉树] lc235. 二叉搜索树的最近公共祖先(dfs+二叉搜索树) 题单: 【题单】链表、二叉树与一般树(前后指针/快慢指针/DFS/BFS/直径/LCA) 二、二叉树 §2.8 最近公共祖先 2. 题目解析 很经典的题目哈,二刷的时候,再注意下非递
代码随想录训练营day34|62.不同路径,63. 不同路径 II,343.整数拆分,96.不同的二叉搜索树
不同路径1 题目 题目并不难想,每一个点只有两种走到的方法,要么从左侧来,要么从上侧来,所以 dp[i][j]=dp[i-1][j]+dp[i][j-1]; vector<vector<int>> dp(m,vector<int>(n,0)); for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(i>0&&j>0){dp[i][j]=dp[i-1][
二叉搜索树的常用操作
参考 :http://blog.csdn.net/wanmeiwushang/article/details/51921821 #include <stdio.h>#include <stdlib.h>typedef enum {false,true}bool;typedef int ElementType;typedef struct TNode* BinTree;stru
深入理解二叉搜索树:在Python中实现插入、删除和查找操作
深入理解二叉搜索树:在Python中实现插入、删除和查找操作 二叉搜索树(BST)是一种重要的数据结构,广泛应用于各种算法和系统中。它不仅支持快速查找,还能高效地进行插入和删除操作。本文将详细介绍如何在Python中实现一个二叉搜索树,并提供插入、删除和查找操作的具体实现。 什么是二叉搜索树? 二叉搜索树是一种特殊的二叉树,满足以下性质: 每个节点的左子树中的所有节点值都小于该节点的值。每
c++ 红黑树(自平衡二叉搜索树)
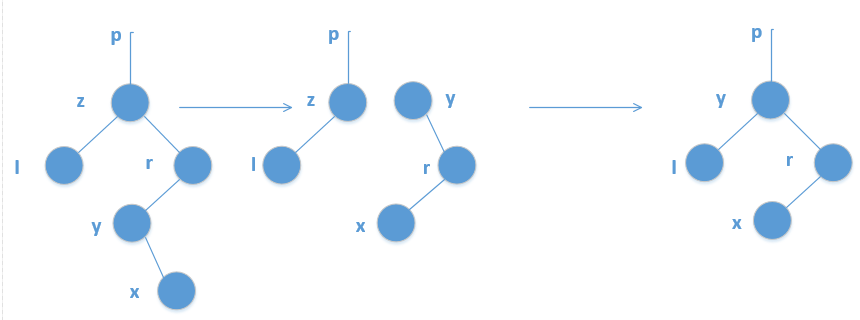
目录 红黑树的概念 红黑树的由来 红黑树的性质 红黑树结点的定义 红黑树的插入 情况一:插入结点的叔叔存在,且叔叔的颜色是红色。 情况二:插入结点的叔叔存在且颜色是黑色 / 叔叔不存在, 情况A:p为g的左孩子,cur为p的左孩子 情况B:p为g的右孩子,cur为p的右孩子 情况C:p为g的左孩子,cur为p的右孩子 情况D:p为g的右孩子,cur为p的左孩子 红黑树
算法day17|530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先
算法day17|算法day17|530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先 530.二叉搜索树的最小绝对差501.二叉搜索树中的众数236. 二叉树的最近公共祖先 530.二叉搜索树的最小绝对差 中间的逻辑有一点小绕,我第一次也做了20分钟左右才发现问题。具体代码如下: class Solution {public:int Mi
二叉搜索树的最近公共祖先:递归与迭代解法全面解析
在本篇文章中,我们将详细解读力扣第235题“二叉搜索树的最近公共祖先”。通过学习本篇文章,读者将掌握如何在二叉搜索树中找到两个节点的最近公共祖先,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述 力扣第235题“二叉搜索树的最近公共祖先”描述如下: 给定一个二叉搜索树,找到该树中两个指定节点的最近公共祖先。 最近公共祖先的定义为:对于有根树 T 的两