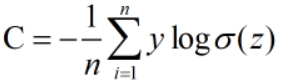mse专题
数学基础 -- 均方误差(Mean Squared Error, MSE)与交叉熵(Cross-Entropy)的数学原理
均方误差(Mean Squared Error, MSE)与交叉熵(Cross-Entropy)的数学原理 1. 均方误差(Mean Squared Error, MSE) 均方误差主要用于回归问题,度量预测值与实际值之间的平均平方差。其数学公式为: MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i
MSE考研--961--第三部分 计算机系统基础
Outline: 一 、处理器体系结构 内容:CPU中的时序电路、单周期处理器的设计、流水线处理器的基本原理、Data Hazard的处理、流水线设计中的其他问题 二、优化程序性能 内容:优化程序性能、优化编译器的能力和局限性以及表示程序性能、特定体系结构或应用特性的性能优化、限制因素、确认和消除性能瓶颈 三、存储器结构及虚拟存储器 内容:局部性、存储器层级结构、计算机高速缓存器原理、
MSE考研--961--第二部分 软件工程 软件测试
四、软件测试 软件测试及测试用例的概念;单元测试、集成测试、确认测试、系统测试、回归测试的概念;调试的概念、调试与测试的关系;测试覆盖度的概念;白盒测试、黑盒测试的概念;代码圈复杂度的计算方法;白盒测试中的基本路径测试方法;黑盒测试中的等价类划分方法。 1.软件测试及测试用例的概念:软件测试是在规定条件下对程序进行操作,从而发现软件错误,衡量软件质量,对其是否满足需求的需求的评估过程; 测试
残差平方和(RSS)、均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)
残差平方和(RSS) 等同于SSE(误差项平方和) 实际值与预测值之间差的平方之和。 MSE: Mean Squared Error 均方误差是RSS的期望值(或均值); MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。 RMSE 均方根误差:均方根误差是均方误差的算术平方根 MAE :Mean Absolute Error 平均绝对误差是绝对
云原生网关 MSE-Higress
云原生网关 MSE-Higress 什么是云原生网关MSEMSE测评产品文档产品能力产品控制台 MSE与其他网关 什么是云原生网关MSE 在体验云原生网关 MSE-Higress功能之前,先了解一下什么是云原生网关 MSE,简单的说就是MSE就是遵循开源 Ingress/Gateway API 标准的下一代网关产品,是一个面向业界主流开源微服务生态的一站式微服务平台,提供注册配置
ImportError: cannot import name ‘compare_mse‘ from ‘skimage.measure‘
问题描述 在复现模型代码的时候遇到错误:ImportError: cannot import name 'compare_mse' from 'skimage.measure' 。 解决方案 这是由于 scikit-image 的版本问题,由于scikit-image版本升级后就修改了库函数。 方法1(修改scikit-image版本,不推荐): pip install sci
sklearn【MSE】均方误差,原理及学习代码!
一、MSE 介绍 均方误差(Mean Squared Error,MSE)是回归问题中常用的一个评估指标,它通过计算预测值与实际值之间差异的平方的平均值来评估模型的精度。 在Python的机器学习库sklearn中,我们可以使用内置的mean_squared_error函数来计算MSE。 具体来说,MSE的计算步骤如下: 收集数据:首先,我们需要一组包含实际目标值(真实值)和模型预测值的数
[机器学习] Pytorch19种损失函数理解[上]— L1、MSE、CrossEntropy、KL、BCE、BCEWithLogits loss function
损失函数通过torch.nn包实现。 文章目录 1 基本用法2 损失函数(前6种)2-1 L1范数损失 —— L1_Loss2-2 均方误差损失 —— MSELoss2-3 交叉熵损失 CrossEntropyLoss2-4 KL 散度损失 KLDivLoss2-5 二元交叉熵损失 BCELoss2-6 BCEWithLogitsLoss 1 基本用法 criterion =
[机器学习] SSE,MSE,RMSE,R-square指标讲解
参考:https://blog.csdn.net/l18930738887/article/details/50629409 SSE(和方差、误差平方和):The sum of squares due to error MSE(均方差、方差):Mean squared error RMSE(均方根、标准差):Root mean squared error R-square(确定系数):Coeffi
【图像去噪】基于matlab GUI均值+中值+高斯低通+多种小波变换图像去噪(含PSNR和MSE)【含Matlab源码 856期】
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。 🍎个人主页:海神之光 🏆代码获取方式: 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭:行百里者,半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理(进阶版) 路径规划(Matlab) 神经网络预测与分类(Matlab) 优化求解(Matlab) 语音处理(Matlab
深度学习代码|MSE损失的代码实现
文章目录 一、MSE代码手动实现(一)导入相关库(二)计算均方误差损失函数(三)示例使用 二、Pytorch中MSELoss函数的接口(一)参数(二)使用示例(三)反向传播 一、MSE代码手动实现 (一)导入相关库 NumPy 是 Python 语言的一个第三方库,支持大量高维度数组与矩阵运算。此外,NumPy 也针对数组运算提供大量的数学函数。机器学习涉及到大量对数组的
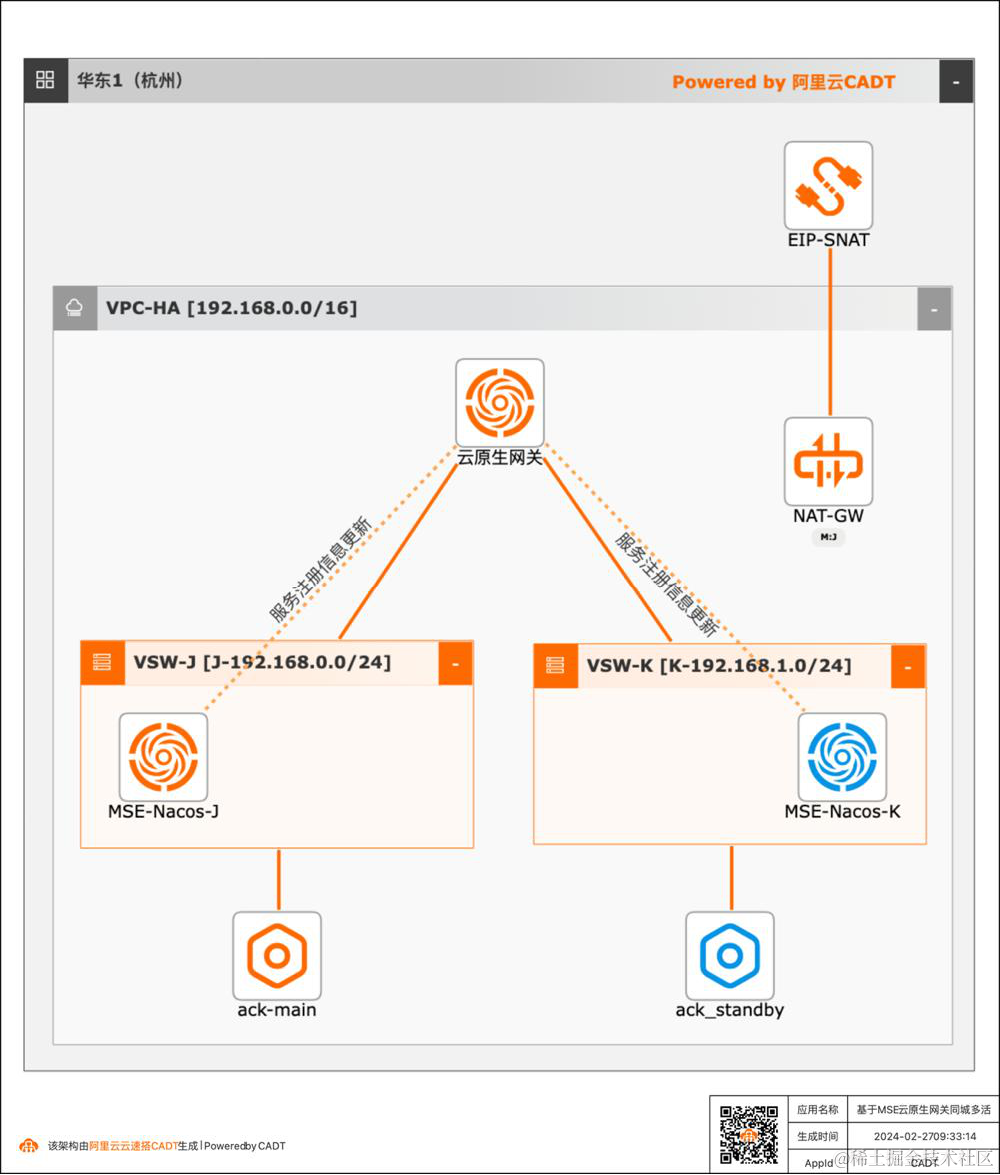
云原生最佳实践系列2:基于 MSE 云原生网关同城多活
方案概述 分布在同城多个机房内的应用同时对外提供服务。同城机房物理距离较小,一般小于 50 公里。同城多活架构的难点有三个: 当某机房出现故障,能不能做到机房级的快速切换?如何实现非对等部署下的全局的流量负载均衡?对流量的精细化管控? 常见的同城多活实现方式(如下图),在这个架构里。DNS 本身存在缓存,DNS 的域名是映射到机房的网关 IP,网关又是每个机房一个局部的。很难做到机房级故障的
转载的 损失函数MSE L1 优化函数ADAM SGD 优化算法等
如有侵权,请联系删除! pytorch框架中损失函数与优化器介绍: 目录 1. 损失函数: 1.1 nn.L1Loss 1.2 nn.SmoothL1Loss 1.3 nn.MSELoss 1.4 nn.BCELoss 1.5 nn.CrossEntropyLoss 1.6 nn.NLLLoss 1.7 nn.NLLLoss2d 2.优化器Optim 2.1 使用 2
MSE v4.3.216
微软杀毒软件。支持系统环境:XP SP3、Vista、Win7。 32位系统:http://download.microsoft.com/download/1/E/D/1ED80C09-218B-44D7-B72D-E1451634E72D/ZHCN/x86/MSEInstall.exe 64位系统:http://download.microsoft.com/download/1/E/D/1E
浏览器采用MSE+FMP4播放海康、大华摄像头RTSP视频流
简述 主要用于解决摄像头视频流无法在WEB上直接显示的需求,网上很多方案涉及的东西较多且复杂,多次转码导致延时较高,直接使用HTML5支持的技术才是上上之选,无插件、无依赖、轻量级。 技术结构 RTSP + H264 + FMP4 + WebSocket + MSE + WEB目前支持海康、大华摄像头RTSP视频流在WEB页面上显示,亲测有效视频流获取支持TCP/UDP两种方式,任意切换通讯库
C++使用OpenCV时计算MSE
前言 OpenCV —— Open Source Computer Vision OpenCV是一个跨平台的计算机视觉库。是由英特尔公司发起并参与开发,以BSD许可证授权发行,可以在商业和研究领域中免费使用。可用于开发实时的图像处理、计算机视觉以及模式识别程序。 在图像处理任务中,评价图像质量标准一般使用MSE(Mean Square Error ,均方误差)和 PSNR(Peak Si
分类问题为什么用交叉熵损失不用 MSE 损失
本文说明以下问题 MSE 损失主要适用与回归问题,因为优化 MSE 等价于对高斯分布模型做极大似然估计,而简单回归中做服从高斯分布的假设是比较合理的交叉熵损失主要适用于多分类问题,因为优化交叉熵损失等价于对多项式分布模型做极大似然估计,而多分类问题通常服从多项式分布 事实上,最大似然估计往往将损失建模为负对数似然,这样的损失一定等价于定义在训练集上的经验分布和定义在模型上的概率分布间的交叉熵
【图像去噪】基于matlab非局部均值(NLM)滤波图像去噪(PSNR和MSE)【含Matlab源码 420期】
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。 🍎个人主页:海神之光 🏆代码获取方式: 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭:行百里者,半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理(进阶版) 路径规划(Matlab) 神经网络预测与分类(Matlab) 优化求解(Matlab) 语音处理(Matlab
损失函数为什么使用交叉熵多而不是MSE(均方差)?
MSE为非凸函数,存在多个极值点,很可能找不到最优解 ,会出现局部最优,不适合作为损失函数 Convex Optimization——凸函数 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/56876303
STATA计算AIC、BIC、MSE、MAE、MAPE值
用STATA做普通的回归时,计算AIC、BIC、MSE、MAE、MAPE并不难,甚至像MSE这样的都会直接给出,但是比如做logit、probit或者mlogit、mprobit甚至ologit、oprobit时,上述五个就不太容易了,在网上搜集了很久,也走了不少弯路。现将方法及代码整理如下: 1.计算AIC、BIC 在做完回归后,紧跟 estat ic 即可得到AIC、BIC 忘记在哪
MSE,MAE和CE的区别
MSE和MAE的区别 异常值 MSE对异常值敏感,因为它的Cost是平方的,所以异常值的loss会非常大,下面的公式中y表示标注,a表示网络预测值。 MAE对异常之不敏感, 不妨设拟合函数为常数,那么MSE就相当于所有数据的均值(列出loss对c求导即可),而MAE相当于所有数据的中位数,所以会对异常值不敏感。 优化效率 MAE不可导而且所有的导数的绝对值都相同,优化时无法确定更
matlab 计算图像的峰值信噪比PSNR以及均方根误差MSE
简介 PSNR 是最普遍,最广泛使用的评鉴画质的客观量测法,不过许多实验结果都显示,PSNR 的分数无法和人眼看到的视觉品质完全一致,有可能 PSNR 较高者看起来反而比PSNR 较低者差。 这是因为人眼的视觉对于误差的敏感度并不是绝对的,其感知结果会受到许多因素的影响而产生变化(例如:人眼对空间频率较低的对比差异敏感度较高,人眼对亮度对比差异的敏感度较色度高,人眼对一个区域的感知结果会受到其周围
FOJ Problem 1075 分解素因子 (筛法求素数Problem 1075 分解素因子 Accept: 1650 Submit: 3102 Time Limit: 1000 mSe)
Problem 1075 分解素因子 Accept: 1650 Submit: 3102 Time Limit: 1000 mSec Memory Limit : 32768 KB Problem Description 假设x是一个正整数,它的值不超过65535(即1<x<=65535),请编写一个程序,将x分解为若干个素数的乘积。 Input 输入的第一行含一个正整数
科赛网新人赛-员工满意度预测 MSE 0.02882
科赛网新人赛-员工满意度预测 - 竞赛思路 原贴地址项目地址 文章目录 科赛网新人赛-员工满意度预测 - 竞赛思路有用的资料、文档、博客环境与工具1.0 基础知识1.1 数据挖掘流程: 2.0 数据探索性分析2.1 单变量分析2.2 多变量分析 3.0 特征工程3.1 特征创建3.1.1 笛卡尔积特征创建3.1.2 使用 number_project 对 average_month
MSE,ks,mAP,weight decay等名词解释
参考链接:http://blog.sina.com.cn/s/blog_57a1cae80101bh65.html 均方误差 (Mean Squared Error)均方误差 MSE是网络的性能函数,网络的均方误差,叫"Mean Square Error"。比如有n对输入输出数据,每对为[Pi,Ti],i=1,2,...,n.网络通过训练后有网络输出,记为Yi。 在相同测量条件下进行的





![[机器学习] SSE,MSE,RMSE,R-square指标讲解](https://img-blog.csdnimg.cn/2021061615322688.png)