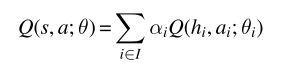decomposition专题

【HDU】5958 New Signal Decomposition【离散对数下的FFT】

题目链接：【HDU】5958 New Signal Decomposition 在此先感谢小q对我的指导，没有q老师的帮助，估计永远也做不出来了。首先我们考虑对这个式子做离散对数。令 g g为pp的某个原根，则有： bi=∑p−1j=0aj⋅r(i,j) \quad b_i=\sum_{j=0}^{p-1}a_j\cdot r(i,j) bi=∑p−1j=0aj⋅2sin32πi⋅j

50个BA分析工具第十一个-Functional Decomposition

知识卡片工具名称： Functional Decomposition（功能分解图）工具介绍：有时会写成Functional Decomposition Diagrams——简称FDD，即功能分解图。它帮助我们管理复杂性，降低不确定性，通过分解流程系统功能领域交付。解决问题： • 大事化小，小事化了。把复杂的东西变成简单的模块，然后去逐一击破。这就是Decomposi

2-8 基于matlab的ESMD（Extreme-Point Symmetric Mode Decomposition）信号分解算法

基于matlab的ESMD（Extreme-Point Symmetric Mode Decomposition）信号分解算法，其基本思想是通过寻找数据序列中的极大值点和极小值点，并以此为基础进行信号分解。该方法在观测数据的趋势分离、异常诊断和时-频分析方面具有独特优势。程序已调通，可直接运行。 2-8 matlab ESMD 信号分解算法 - 小红书 (xiaohongshu.com)

覆盖路径规划经典算法 The Boustrophedon Cellular Decomposition 论文及代码详解

2000年一篇论文 Coverage of Known Spaces: The Boustrophedon Cellular Decomposition 横空出世，解决了很多计算机和机器人领域的覆盖路径问题，今天我来详细解读这个算法。 The Boustrophedon Cellular Decomposition 算法详解这篇论文标题为"Coverage Path Planning: Th

覆盖路径规划经典算法 The Boustrophedon Cellular Decomposition 详解

2000年一篇论文 Coverage of Known Spaces: The Boustrophedon Cellular Decomposition 横空出世，解决了很多计算机和机器人领域的覆盖路径问题，今天我来详细解读这个算法。 The Boustrophedon Cellular Decomposition 算法详解这篇论文标题为"Coverage Path Planning: Th

Face Forgery Detection by 3D Decomposition

文章目录 Face Forgery Detection by 3D Decomposition研究背景研究目标创新点方法提出问题研究过程技术贡献实验结果未来工作 Face Forgery Detection by 3D Decomposition 会议：CVPR2021 作者：研究背景面部伪造引发关注传统面部伪造检测主要关注原始RGB图像

Singular Value Decomposition：奇异值分解(降维)

SVD 降维相似度计算: 1.欧式距离向量的范数2 2.皮尔逊相关系数 cov(X,Y)varxvary c o v ( X , Y ) v a r x v a r y \frac{cov_{(X,Y)}}{var{x} var{y}} 均值意义:样本集合的中间点方差意义: 样本点的离散程度协方差意义: 度量两个随机变量关系的统计量度量各个维度偏离其均值的程度协方差计

[译]sklearn.decomposition.TruncatedSVD

sklearn.decomposition.TruncatedSVD class sklearn.decomposition.TruncatedSVD(n_components=2, algorithm=’randomized’, n_iter=5, random_state=None, tol=0.0) 采用阶段奇异值分解SVD降维。与PCA相比，这种方式再计算SVD之前不指定数据中

Lecture 011-3-Dantzig-Wolfe decomposition

Outline •Fundamental understanding •Lagrangian relaxation & Representation theory •DW & CG •Case application ----------------------------- •列生成算法适用于解决一类候选决策方案可以由多个完全信息下的列表示的组合优化问题。•该算法并不直接对带有所有

10MARL深度强化学习 Value Decomposition in Common-Reward Games

文章目录前言1、价值分解的研究现状2、Individual-Global-Max Property3、Linear and Monotonic Value Decomposition3.1线性值分解3.2 单调值分解前言中心化价值函数能够缓解一些多智能体强化学习当中的问题，如非平稳性、局部可观测、信用分配与均衡选择等问题，然而存在很难直接学习价值函数等问题，特别是动作价值

C#，数值计算，矩阵的乔莱斯基分解（Cholesky decomposition）算法与源代码

一、安德烈·路易斯·乔尔斯基安德烈·路易斯·乔尔斯基出生于法国波尔多以北的查伦特斯海域的蒙古扬。他在波尔多参加了Lycée e，并于1892年11月14日获得学士学位的第一部分，于1893年7月24日获得第二部分。1895年10月15日，乔尔斯基进入莱科尔理工学院，在当年223名入学学生中排名第88位。他在莱科尔理工学院的教授包括卡米尔·乔丹和发现放射性的著名物理学家亨利·贝克勒尔。在

Subgraph Decomposition for Multi-Target Tracking

来源：CVPR2015 创新点：跟踪的常规做法是：首先在空间上选择假设，然后随着时间的推移连接这些假设，在这个过程中需要保证不相交的路径约束。在拥挤场景下，多重假设往往是彼此相似的。基于此，本文提出将时间和空间联合起来，连接合理的检测结果。特别的，将MOT看成是一个最小代价子图多割（a minimum cost subgraph multicut problem）问题。成对的检测假设可以

偏差-方差分解bias-variance decomposition

方差、偏差的直观意义方差维基百科定义： Var ⁡ ( X ) = E [ ( X − μ ) 2 ] 其中 μ = E ( X ) \operatorname{Var}(X)=\mathrm{E}\left[(X-\mu)^{2}\right] 其中\mu=\mathrm{E}(X) Var(X)=E[(X−μ)2]其中μ=E(X) 在给定数据集中方差： var ⁡ ( x ) =

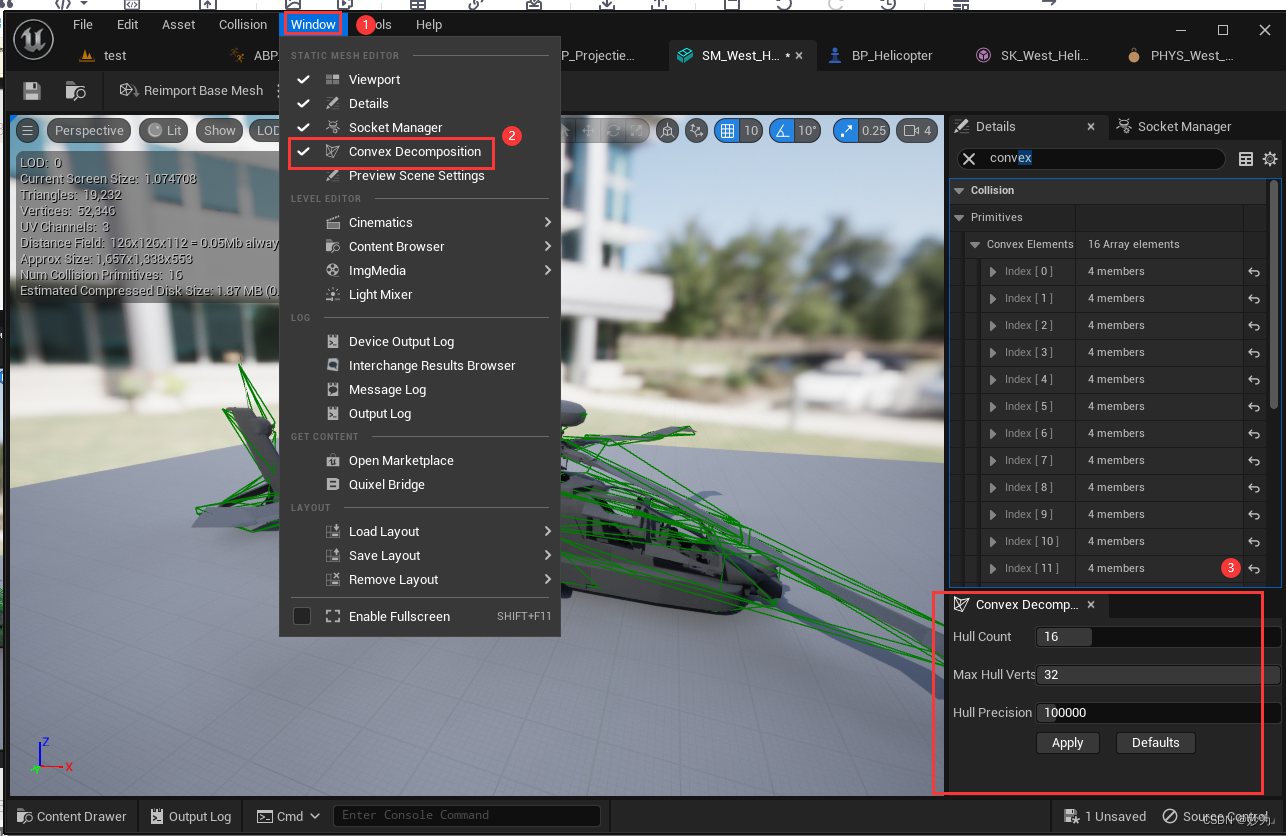
unreal engine5.1中设置convex decomposition凸包分解

UE5系列文章目录文章目录 UE5系列文章目录前言一、convex decomposition是什么？二、convex decomposition属性设置前言今天使用ue5根据网上教程制作可操控直升机，找属性convex decomposition凸包分解，默认的碰撞如下图如果想使用精细化的碰撞检测就要收到设置convex decomposition属性。如下图

方差分解（variance decomposition）研究发展史

方差分解（variance decomposition）研究发展史 1 早期技术概述1.1 方差组分分析（variance components analysis, VCA ）1.2 方差分析（Analysis of Variance，简称ANOVA） 2 交叉嵌套数据结构和早期方差分解技术的局限性3 多层次建模方法的方差分解参考 1 早期技术概述方差分解如下：下面介绍方差

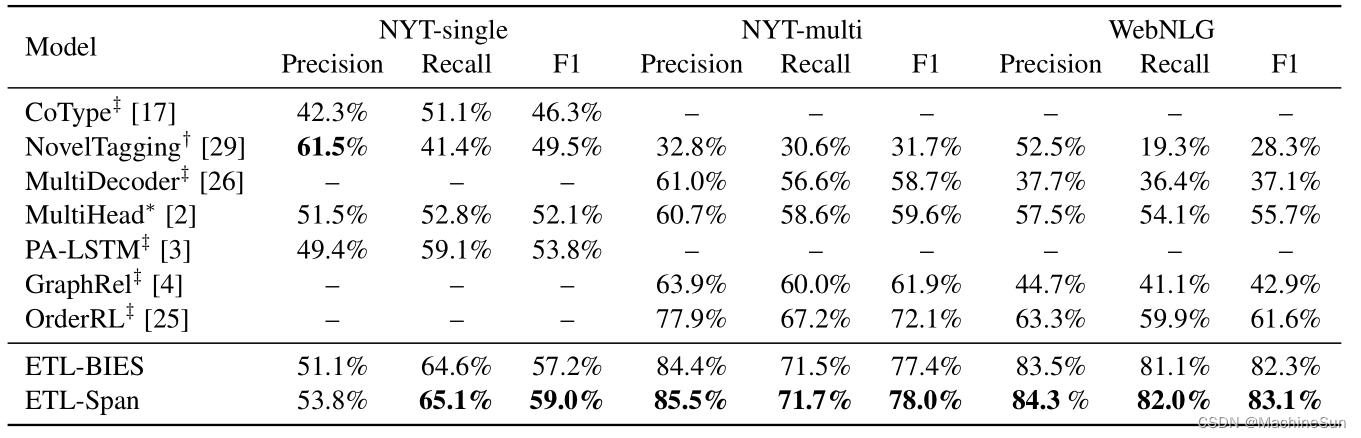
Joint Extraction of Entities and Relations Based on a Novel Decomposition Strategy

Abstract 本文将关系抽取任务转换为两个任务，HE抽取（头实体抽取）和TER抽取（尾实体和关系）前一个子任务是区分所有可能涉及到object关系的头实体，后一个任务是识别每个提取的头实体对应的尾实体和关系，然后基于本文提出的基于span的标记方法将两个子任务进一步分解为多个序列标记任务，采用分层边界标记HBT和多跨度解码算法解决这些问题。本文的第一步不是提取所有实体，而是识别可能参与

固有时间尺度分解（Intrinsic Time Decomposition，ITD）

代码教程固有时间尺度分解(ITD) 代码原理 ITD（Intrinsic Time Decomposition）是一种信号分解方法，用于将信号分解成多个时频组件。它的基本思想是将信号分解为一组原子函数，这些原子函数具有不同的时频特性。 ITD分解的步骤如下：定义一个初始信号x。对初始信号进行一次ITD分解，得到分解后的高频信号和低频信号。判断低频信号是否满足终止条件：如果

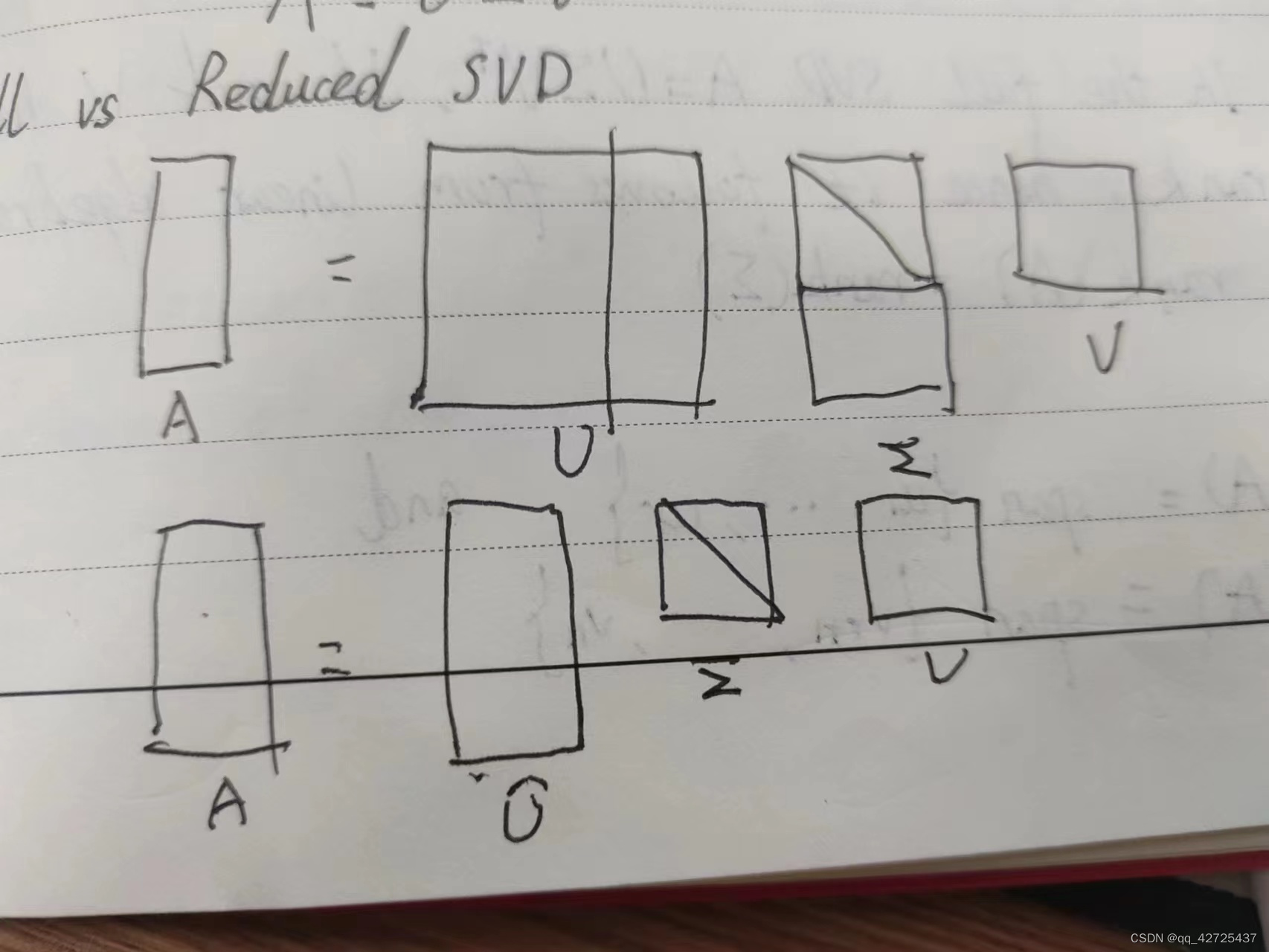
A Singularly Valuable Decomposition(SVD奇异值分解)

A Singularly Valuable Decomposition(SVD奇异值分解) SVD与熟悉的对称矩阵对角化理论密切相关。如果A是对称实数n×n矩阵，则存在正交矩阵V和对角线D，使得A= 。这里V的列是A的特征向量，并形成Rn的正交基; D的对角线上的数值是A的特征值。为了强调与SVD的联系，我们将称为A的特征值分解或EVD。对于SVD，任意一

奇异值分解SVD（singular value decomposition）

奇异值分解 SVD是一个很有用的矩阵因子化方法。 SVD提出的目的：任何一个 m × n m\times n m×n的矩阵都可以当作一个超椭圆（高维空间的椭圆），可以把它们当作单位球体S的像。一个超椭圆可以通过将单位球型在正交方向 u 1 , u 2 , . . . , u m \mathbf{u_1},\mathbf{u_2},...,\mathbf{u_m} u1,u2,...,um

RDGAN Retinex Decomposition Based Adversarial Learning for Low-Light Enhancement（论文阅读笔记）

RDGAN Retinex Decomposition Based Adversarial Learning for Low-Light Enhancement（论文阅读笔记）最近学习了一篇论文《RDGAN Retinex Decomposition Based Adversarial Learning for Low-Light Enhancement》，记录一下概括在本文提出了一种

C#，码海拾贝（17）——对称正定矩阵的乔里斯基分解（Cholesky decomposition）与行列式的求值之C#源代码

31月53日这一天，法国数学家安德烈-路易·乔列斯基在第一次世界大战即将结束时的一场战斗中阵亡，享年<>岁，当时他在法国陆军担任工程军官。他曾担任制图师和大地测量学家，对数学科学的其他贡献之一是Cholesky分解（发现以帮助他的专业），该分解说正定对称矩阵可以分解为较低三角矩阵及其转置的乘积。此属性的其他应用包括求解线性方程组、最小二乘问题、蒙特卡罗模拟和卡尔曼滤波器。在克

逐次变分模态分解(Sequential Variational Mode Decomposition，SVMD)（附代码）

代码原理逐次变分模态分解（Sequential Variational Mode Decomposition，SVMD）是一种用于信号处理和数据分析的方法。它可以将复杂的信号分解为一系列模态函数，每个模态函数代表了信号中的一个特定频率成分。SVMD的主要目标是提取信号中的不同频率成分，并将其重构为原始信号。 SVMD的基本原理是通过变分模态分解的方式将信号分解为多个模态函数。在每个迭代步骤中

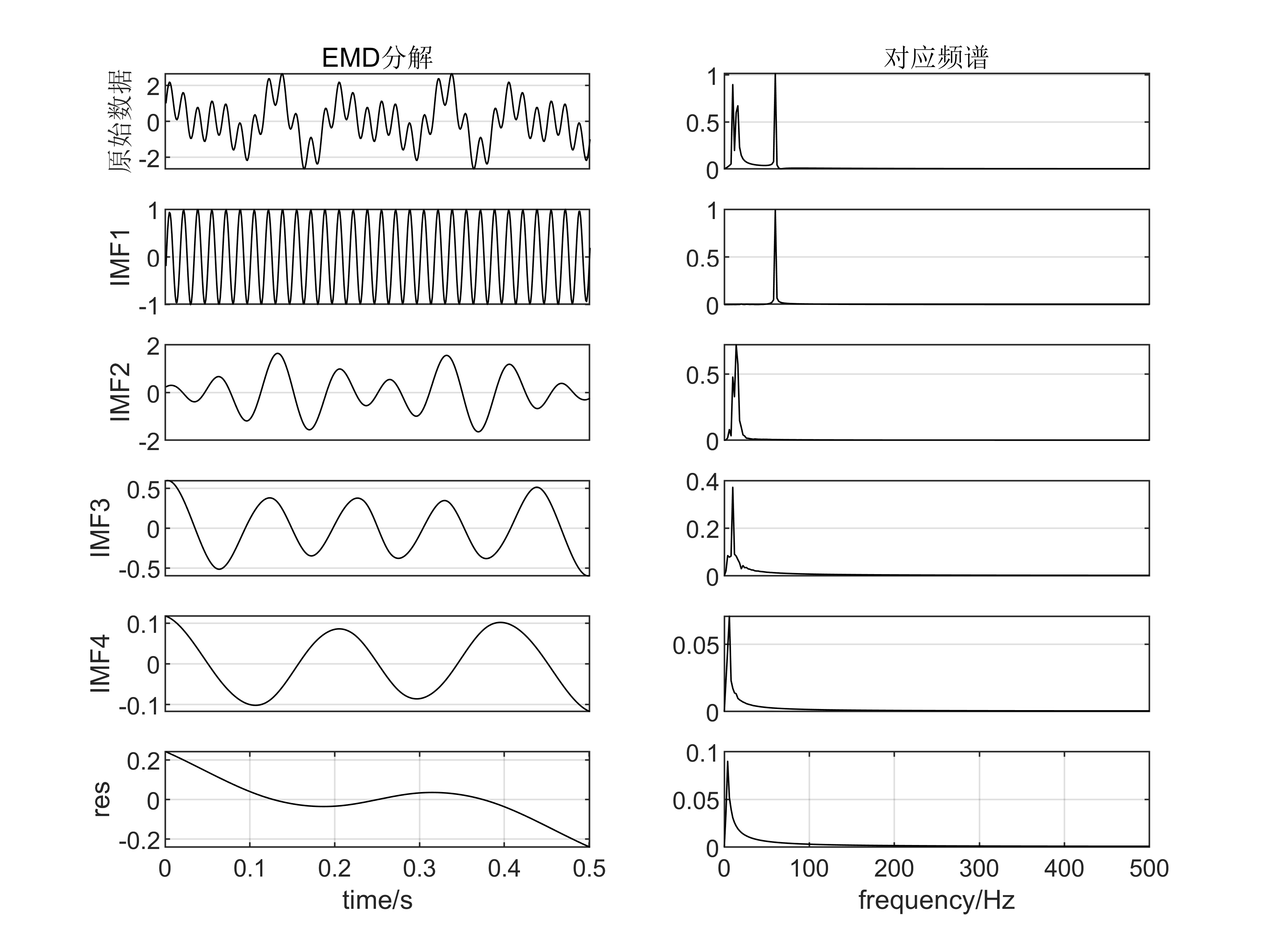
经验模态分解（Empirical Mode Decomposition，EMD）（附代码）

代码原理 EMD（Empirical Mode Decomposition），也称为经验模态分解，是一种将非线性和非平稳信号分解成多个本征模态函数（Intrinsic Mode Functions，简称IMF）的方法。 EMD的基本原理是通过一系列迭代过程将信号分解为一组IMF，其中每个IMF都满足以下两个条件： 1. 在整个信号上的极值点数目相同或最多相差一个。 2. 在任何点上，通过I

Column-and-constraint generation VS Benders‘ decomposition

论文地址：Solving two-stage robust optimization problems using a column-and-constraint generation method 之前介绍过一个column-and-row generation方法，这次介绍一个更加常用的Column-and-constraint generation（C&CG）。从论文题目就可以看出，这

Matrix Decomposition矩阵分解大比拼：性能、应用场景和可视化对比总结

在机器学习领域，矩阵分解是一种常用的技术，用于从复杂数据中提取有用的信息。Cross decomposition 是一种特殊的矩阵分解方法，它用于找到两个矩阵之间的一种或多种关系。这种方法在多个应用场景中非常有用，例如推荐系统、自然语言处理和图像识别等。文章目录 Matrix Decomposition性能对比应用场景对比数据可视化选择优缺点对比性能评估sklearn 零基础入门总结

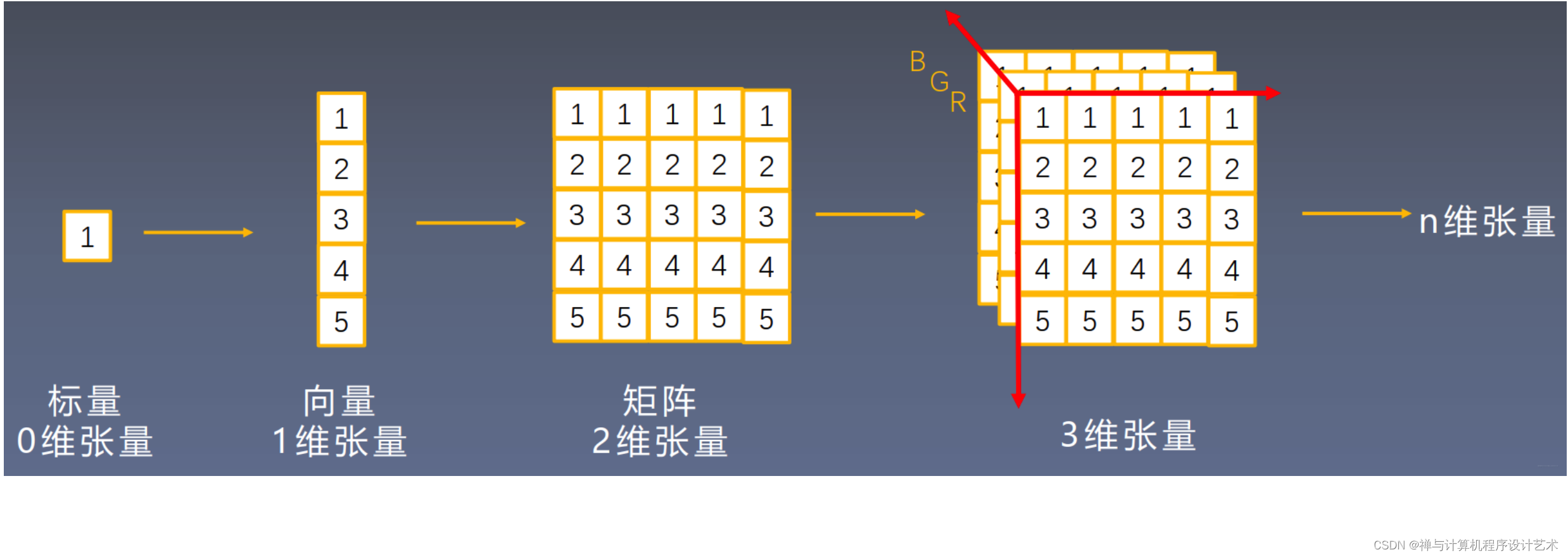
【人工智能的数学基础】张量分解(Tensor Decomposition)

【人工智能的数学基础】张量分解(Tensor Decomposition) 文章目录【人工智能的数学基础】张量分解(Tensor Decomposition)张量的概念张量分解1. Tucker分解2. CP分解3. 应用：缺失数据修复 Tensor Decomposition(Factorization). 张量的概念张量是一种数学对象，它可以用来描述物理现象