本文主要是介绍Lecture 011-3-Dantzig-Wolfe decomposition,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Outline
•Fundamental understanding
•Lagrangian relaxation & Representation theory
•DW & CG
•Case application
-----------------------------
•列生成算法适用于解决一类候选决策方案可以由多个完全信息下的列表示的组合优化问题。•该算法并不直接对带有所有列的规划问题进行求解,而是通过限制主问题求解只包含当前生成列的模型,再由列生成子问题选择可能改进限制主问题目标函数值的列,并加入到限制主问题中。•该算法的优点在于最后没有被子问题生成的列被判定为不会改进限制主问题的当前最优解,所以避免了考虑大量可能的列。
-------------------------------
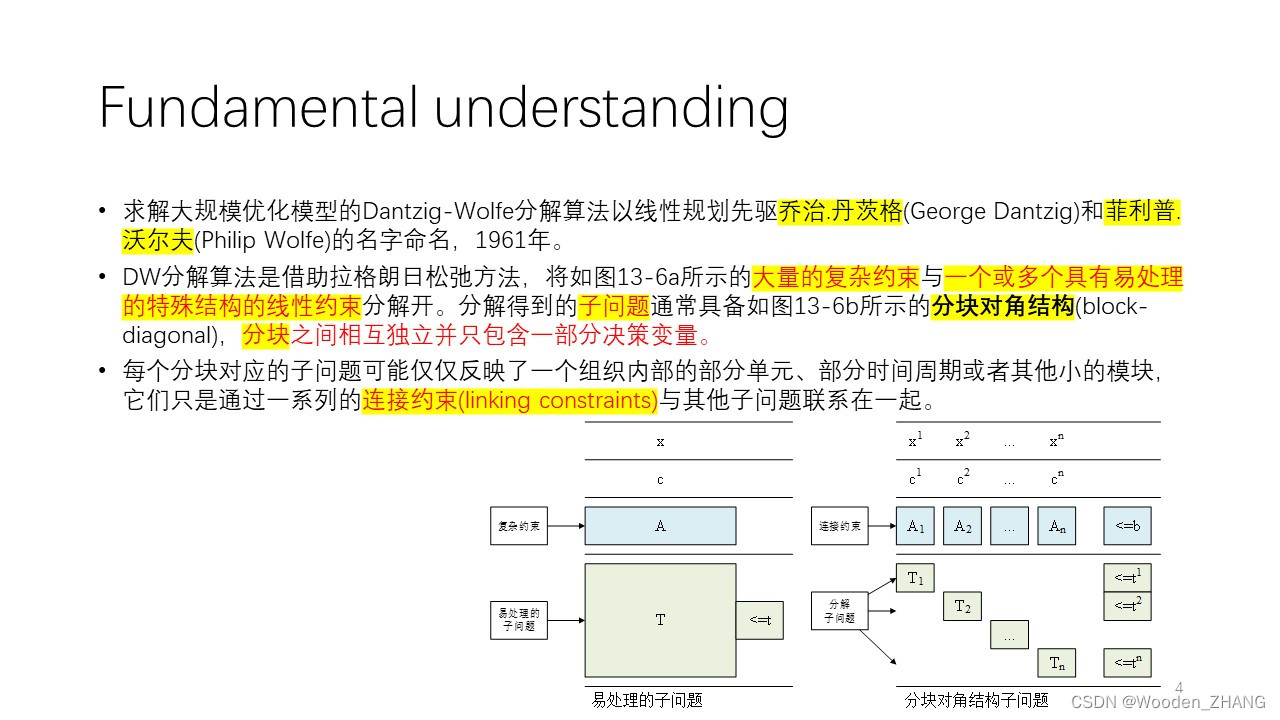
•求解大规模优化模型的Dantzig-Wolfe分解算法以线性规划先驱乔治.丹茨格(GeorgeDantzig)和菲利普.沃尔夫(PhilipWolfe)的名字命名,1961年。
•DW分解算法是借助拉格朗日松弛方法,将复杂约束与一个或多个具有易处理的特殊结构的线性约束分解开。
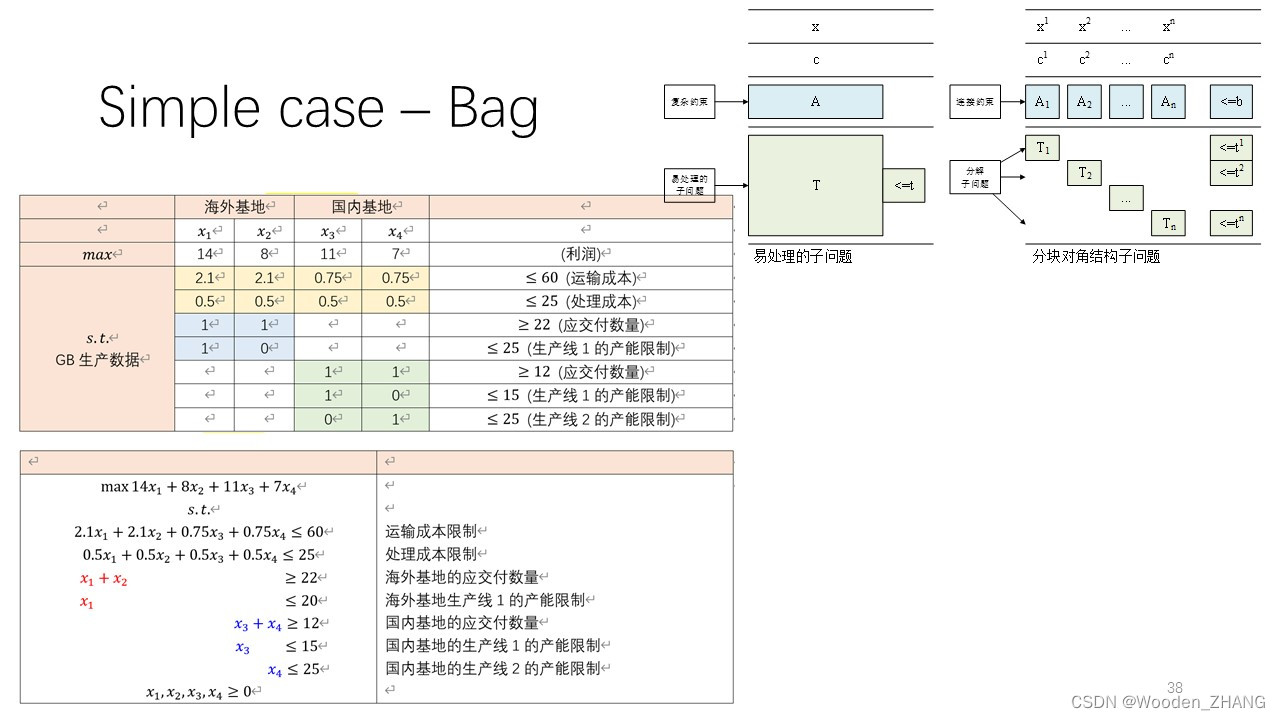
分解得到的子问题通常具备分块对角结构(block-diagonal),分块之间相互独立并只包含一部分决策变量。•每个分块对应的子问题可能仅仅反映了一个组织内部的部分单元、部分时间周期或者其他小的模块,它们只是通过一系列的连接约束(linkingconstraints)与其他子问题联系在一起。•
-----------------------------------------------
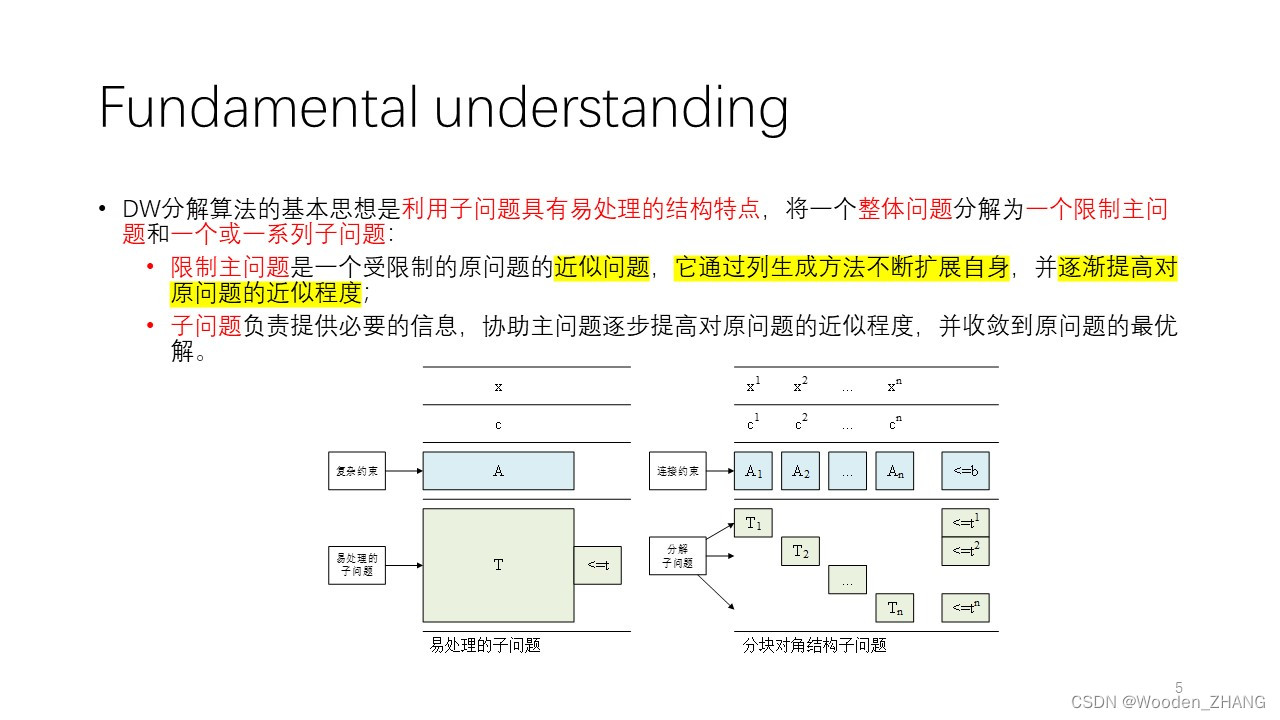
•DW分解算法的基本思想是利用子问题具有易处理的结构特点,将一个整体问题分解为一个限制主问题和一个或一系列子问题:
•限制主问题是一个受限制的原问题的近似问题,它通过列生成方法不断扩展自身,并逐渐提高对原问题的近似程度;
•子问题负责提供必要的信息,协助主问题逐步提高对原问题的近似程度,并收敛到原问题的最优解。•
------------------------

































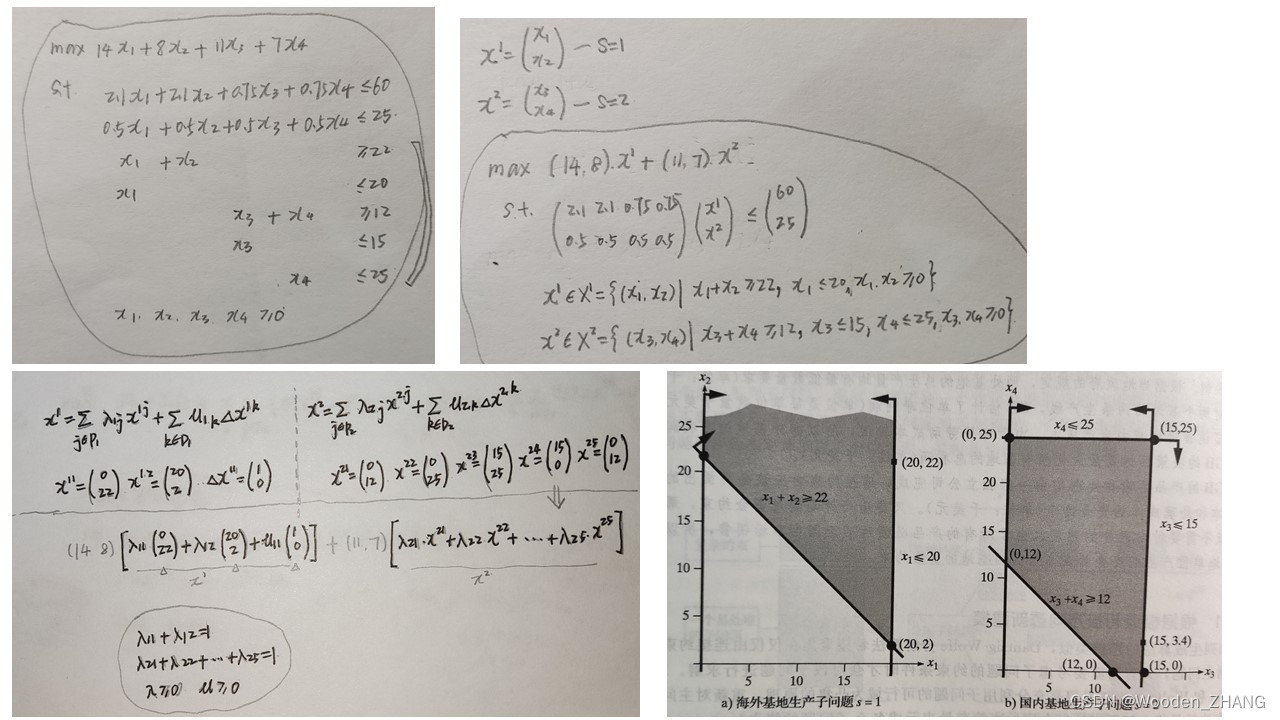





这篇关于Lecture 011-3-Dantzig-Wolfe decomposition的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!