MEMS：Lecture 18 Feedback

本文主要是介绍MEMS：Lecture 18 Feedback，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

讲义

Linear feedback

MEMS热板 Hotplate

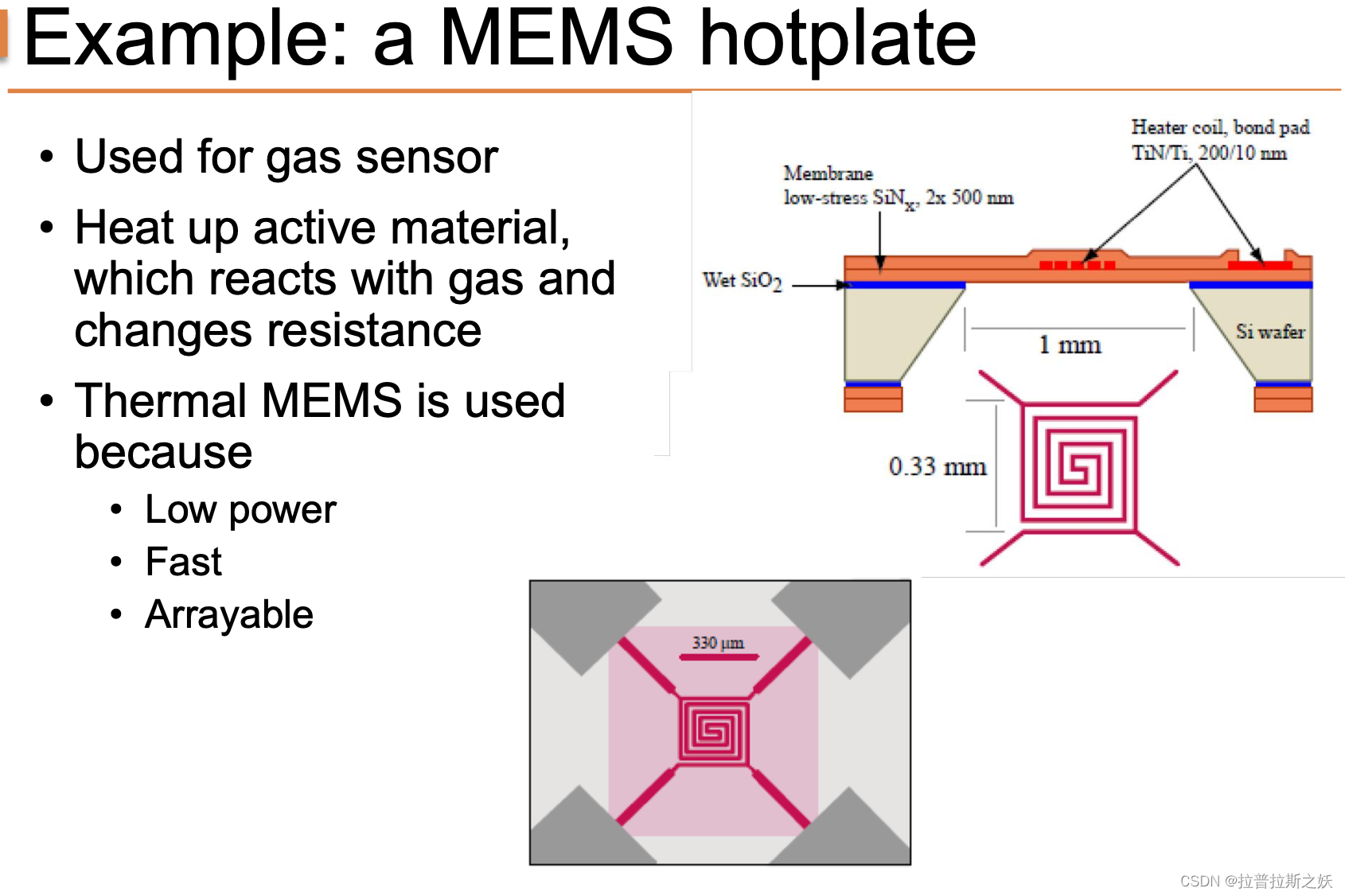
MEMS（微机电系统）热板是现代气体传感器的重要组成部分。它们通过加热一种活性材料来工作，这种材料与气体发生反应，从而改变其电阻。电阻的变化可以用来检测和测量特定气体的存在和浓度。

MEMS热板通常由以下几个部分组成：

• 加热元件：通常是由薄金属膜（如钛/钛氮化物）构成的螺旋形加热器。这些加热器被设计成能够快速且均匀地升温，以确保活性材料能够迅速与气体反应。
• 膜片：由低应力氮化硅（SiNx）制成，厚度约500纳米。膜片的作用是作为加热元件的支撑结构，同时尽可能减少热损失。
• 基底：通常是硅片（Si wafer），其上覆盖有湿法氧化硅（Wet SiO2），起到绝缘作用。

这种结构设计的优点在于低功耗、快速响应和可阵列化。低功耗是由于MEMS技术的微小尺寸和高效设计；快速响应是因为热板的加热和冷却速度很快；可阵列化则允许多个热板集成在一个芯片上，增加了传感器的灵敏度和功能。

MEMS热板常用于气体传感器中，通过加热活性材料（如金属氧化物），使其与环境中的气体发生化学反应。这种反应会导致材料的电阻变化，从而可以检测到气体的种类和浓度。例如，在检测有毒气体、一氧化碳或其他工业污染物时，MEMS热板可以提供快速和可靠的检测方法。

反馈控制系统

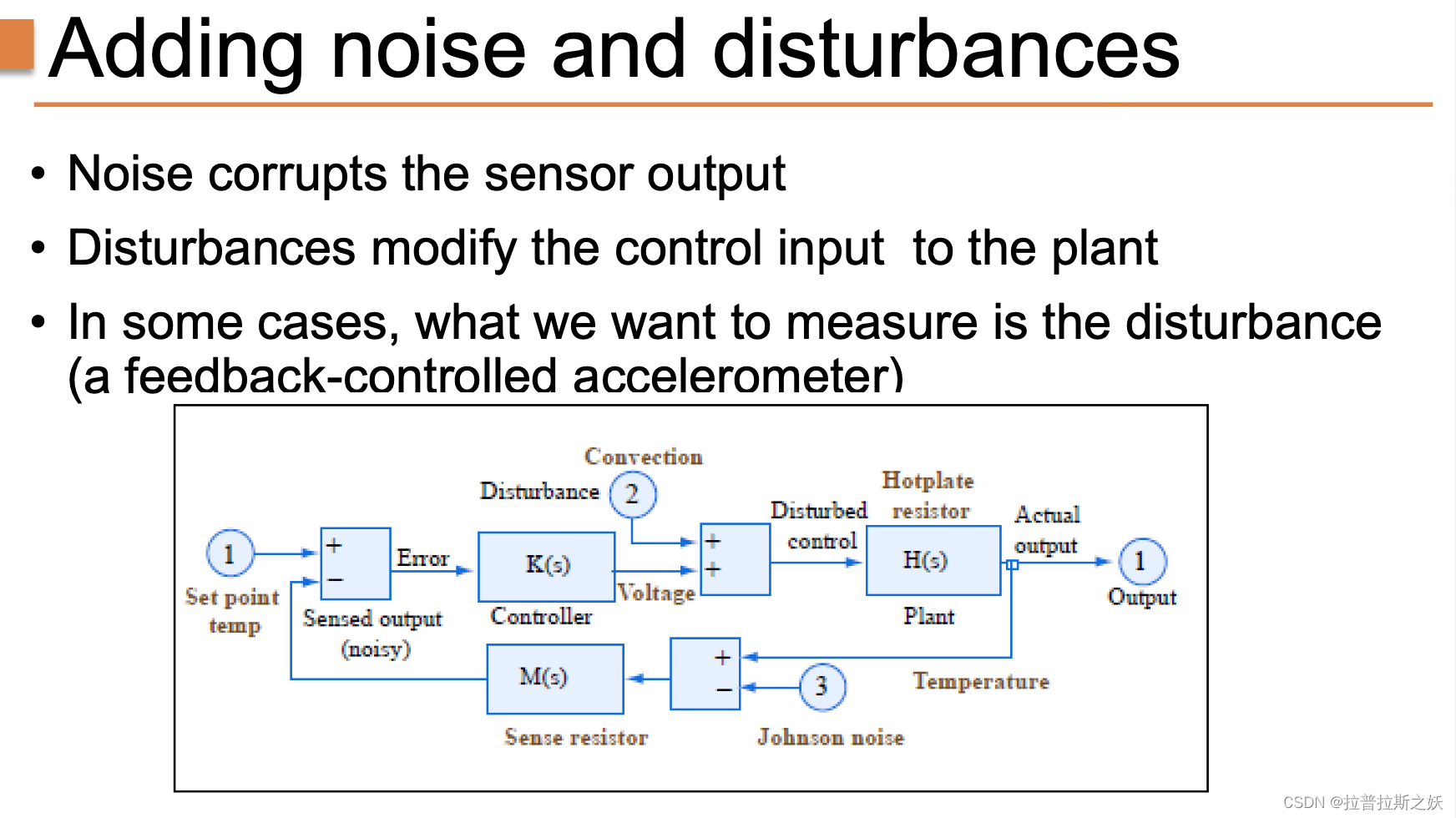
扰动会修改传递到执行机构的控制输入，使得实际执行的操作与预期不符。扰动可以是环境变化、系统内部非理想特性或者外部干扰等。一个常见的例子是热板系统中的对流扰动，热量通过对流方式散失，导致热板温度难以稳定在设定值。

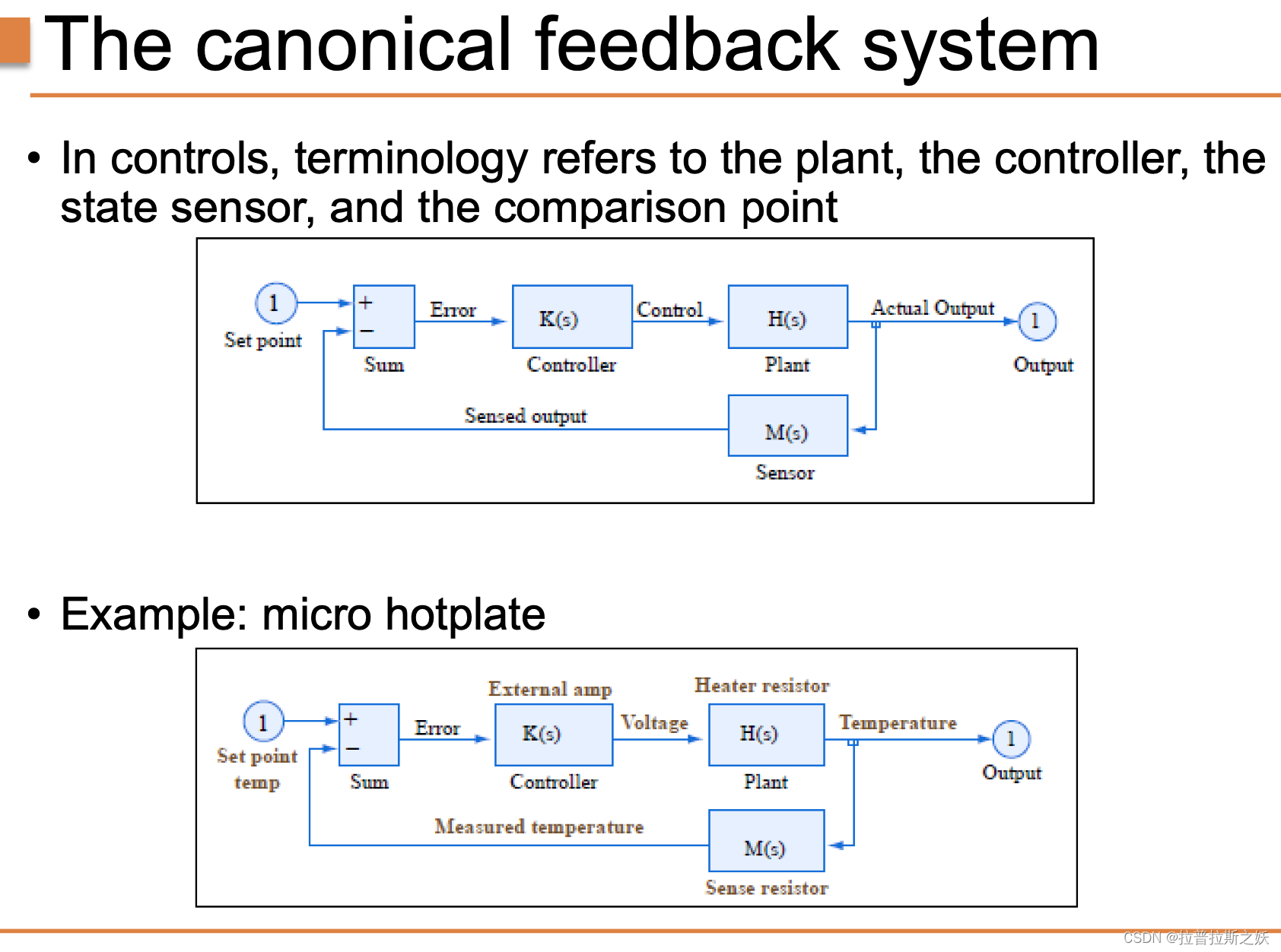
反馈控制系统由以下几个基本部分组成：

• 设定点（Set point）：系统期望达到的目标值。
• 误差（Error）：设定点与实际输出之间的差异。
• 控制器（Controller）：根据误差信号生成控制信号，以调整系统的输出。
• 执行机构（Plant）：实际进行控制操作的部分。
• 传感器（Sensor）：检测系统输出的实际值。

以微型热板为例，该系统的反馈控制流程如下：

1. 设定温度：用户设定一个期望的温度值（设定点）。
2. 温度测量：传感器测量热板的实际温度。
3. 误差计算：控制器计算设定温度与实际温度之间的差异（误差）。
4. 生成控制信号：控制器根据误差生成适当的控制信号，调整加热元件的功率输出。
5. 温度调整：加热元件根据控制信号调整温度，直到实际温度与设定温度一致。

通过这种反馈控制系统，可以确保微型热板在各种环境条件下都能精确维持所需的温度。

闭环传递函数：Black公式

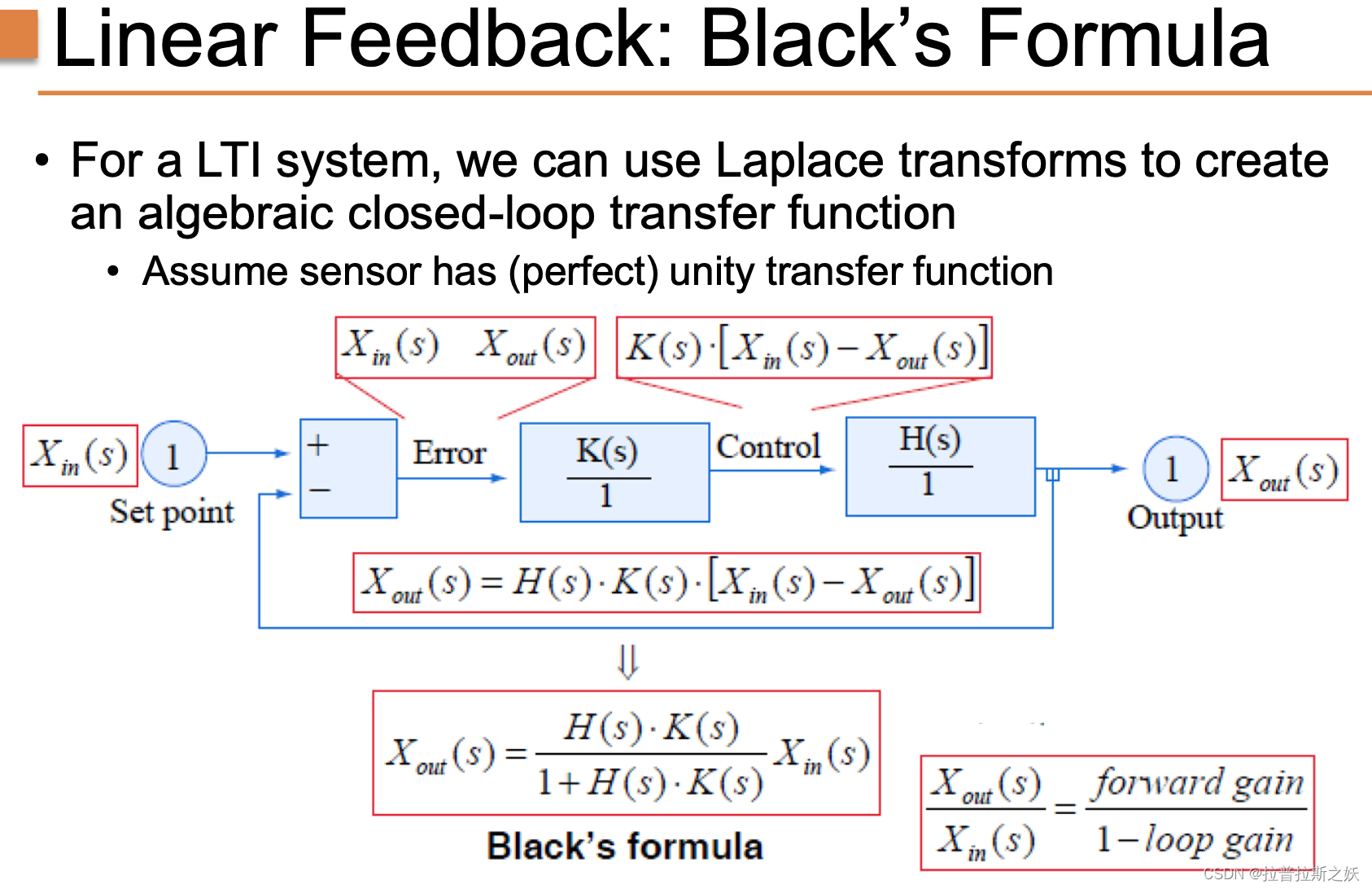
线性时不变系统（LTI系统）中的反馈控制可以通过拉普拉斯变换（Laplace transform）来分析和设计。Black公式提供了一个闭环传递函数的代数表示，使得可以定量地分析系统的稳定性和性能。

假设传感器具有理想的单位传递函数，系统的闭环传递函数可以表示为：

$$X_{out}(s)=H(s)\cdot K(s)\cdot [X_{in}(s)-X_{out}(s)]$$

经过代数变换，可以得到：

$$X_{out}(s)=\frac{H(s)\cdot K(s)}{1+H(s)\cdot K(s)}\cdot X_{in}(s)$$

这就是所谓的Black公式，用于描述闭环系统的输出与输入之间的关系：

$$\frac{X_{out}(s)}{X_{in}(s)}=\frac{forwardgain}{1-loopgain}$$

其中：

• forward gain：前向增益，由传感器和控制器的增益决定。
• loop gain：环路增益，是系统稳定性的重要指标。

通过这个公式，可以分析系统在不同增益条件下的行为，评估系统的稳定性和动态响应。

开环操作（Open-loop Operation）

开环控制系统虽然结构简单，但对扰动和系统参数变化的敏感性较高，难以保证控制精度。在实际应用中，常常需要采用闭环控制系统，通过反馈机制来实时调整控制输入，抵消扰动的影响，提高系统的稳定性和精度。

在控制系统中，开环操作是一种不依赖反馈信号的控制方式。这意味着系统的输出不被用来调整控制输入。开环系统通常用于简单、稳定且对外界扰动不敏感的应用场景。

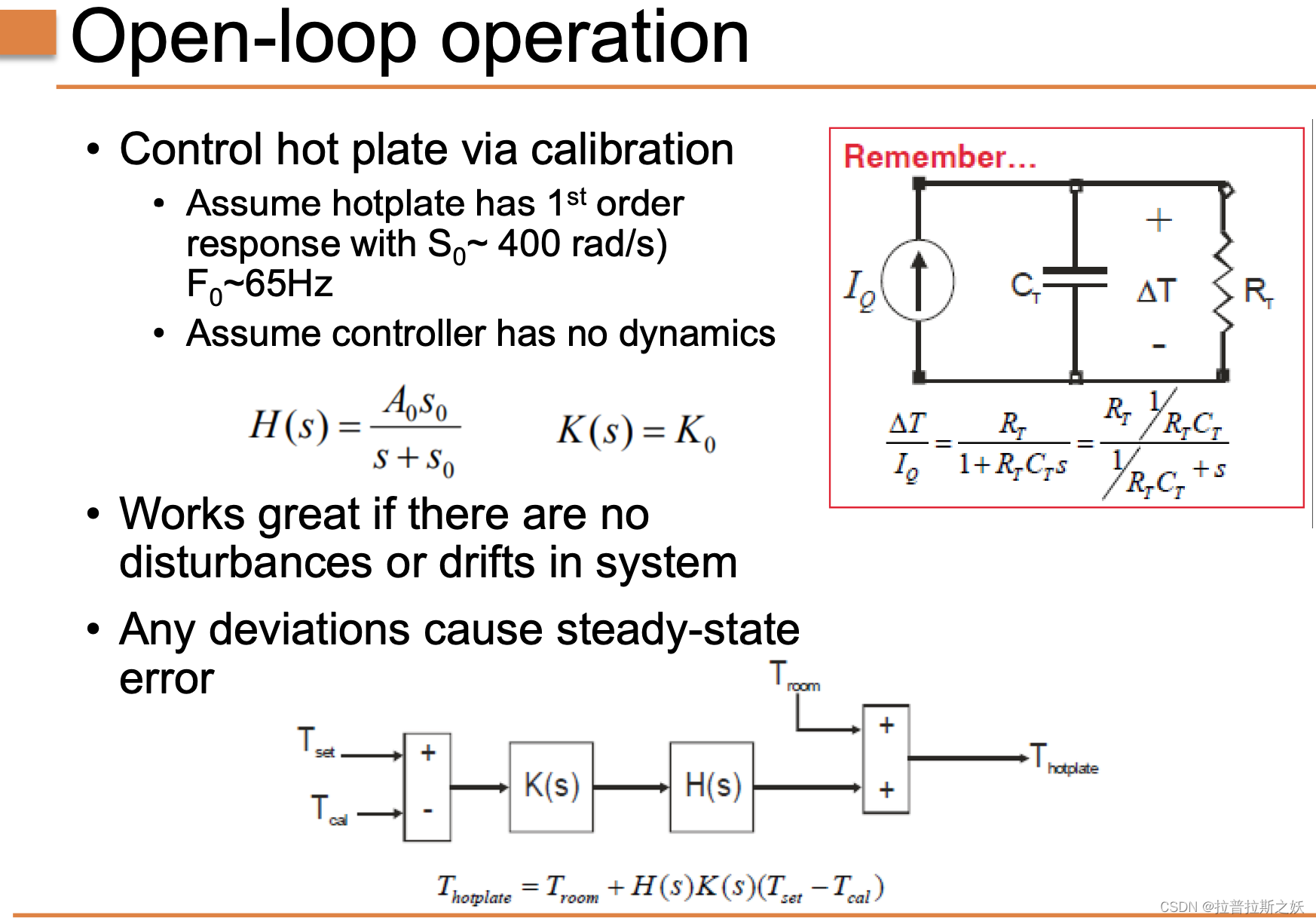
图中的开环操作示例展示了如何通过校准来控制热板的温度：

• 假设热板具有一阶响应：响应频率 $S_0\approx 400\text{rad/s}$ 和频率 $F_0\approx 65\text{Hz}$。
• 假设控制器无动态特性：即控制器输出与输入之间是线性关系，没有延迟或其他动态因素。

系统传递函数 $H(s)$ 和控制器传递函数 $K(s)$ 分别为：

$$H(s)=\frac{A_0{s}_0}{s+s_0}$$
$$K(s)=K_0$$

开环控制系统的优点在于其设计和实现简单。然而，这种系统仅在没有扰动或漂移的情况下才能正常工作。一旦系统出现偏差（如环境温度变化或系统参数漂移），则会产生稳态误差，无法通过调整控制输入来纠正。

右侧的电路图展示了热板的等效电路模型。电路中的热阻 $R_T$ 和热容 $C_T$ 构成了一个一阶系统，其传递函数为：

$$\frac{\Delta T}{I_Q}=\frac{R_T}{1+R_T{C}_{T}s}=\frac{R_T}{1/R_T{C}_T+s}$$

图中下方的框图展示了开环控制系统的结构。系统的输出温度 $T_{\text{hotplate}}$ 可以表示为：

$$T_{\text{hotplate}}=T_{\text{room}}+H(s)K(s)(T_{\text{set}}-T_{\text{cal}})$$

其中：

• $T_{\text{set}}$：设定温度。
• $T_{\text{cal}}$：校准温度。
• $T_{\text{room}}$：环境温度。

响应对控制器、执行机构和扰动的敏感性

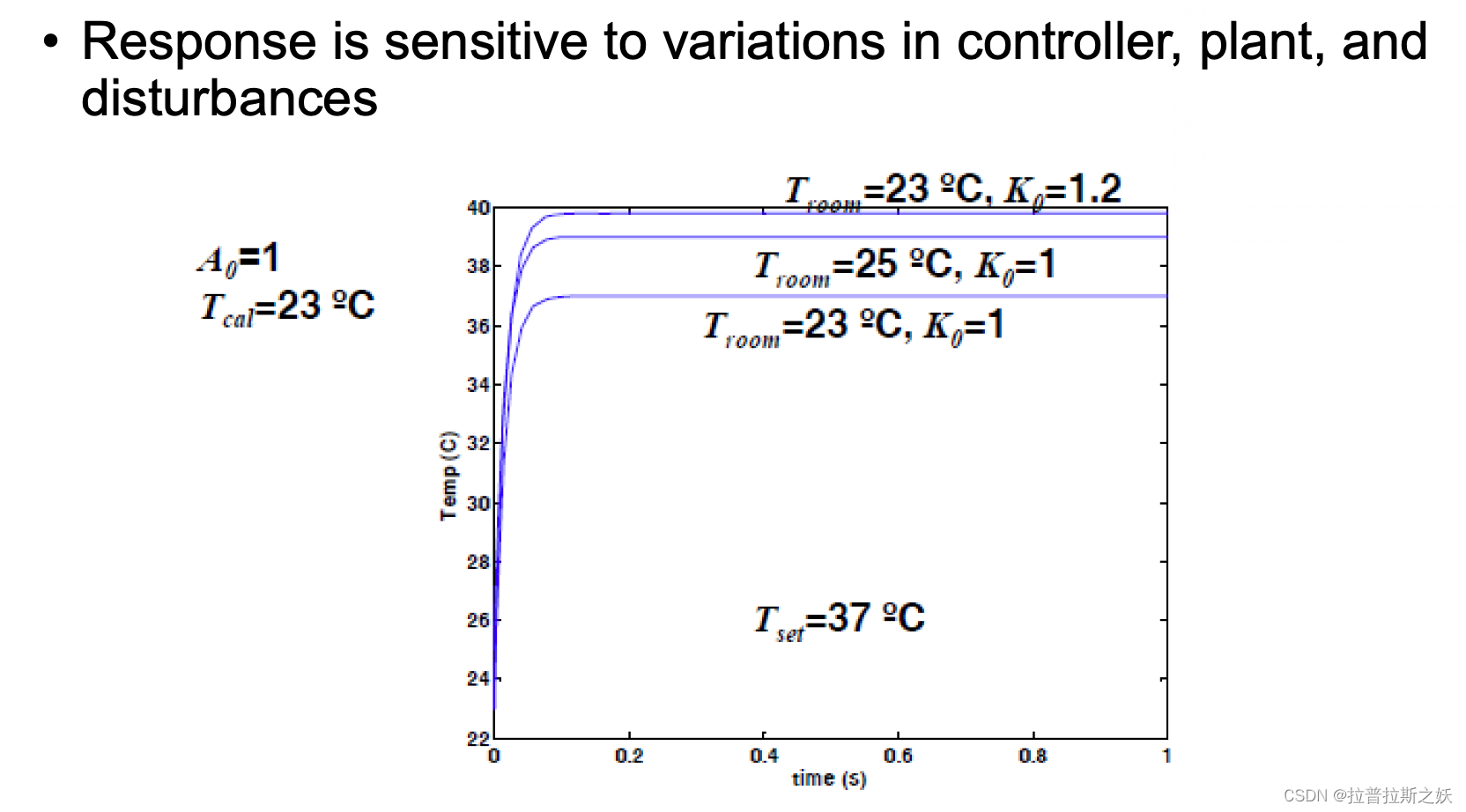
开环系统对控制器参数、执行机构特性和外界扰动非常敏感。图中的曲线展示了不同条件下系统的温度响应：

• 系统参数 $A_0=1$，校准温度 $T_{\text{cal}}=23\text{°C}$。
• 环境温度变化： $T_{\text{room}}=23\text{°C}$ 和 $T_{\text{room}}=25\text{°C}$。
• 控制增益变化： $K_0=1$ 和 $K_0=1.2$。

可以看到，当环境温度或控制增益发生变化时，系统的响应曲线也会发生显著变化。这说明开环系统在实际应用中难以保证精确控制，特别是在外界条件复杂多变的情况下。

闭环控制

通过反馈控制，系统可以显著提高对变化的鲁棒性和响应速度。比例控制通过增加误差比例项，使系统能够抵抗外界扰动和参数变化。而增加控制增益则可以提高系统的带宽，加快响应速度。
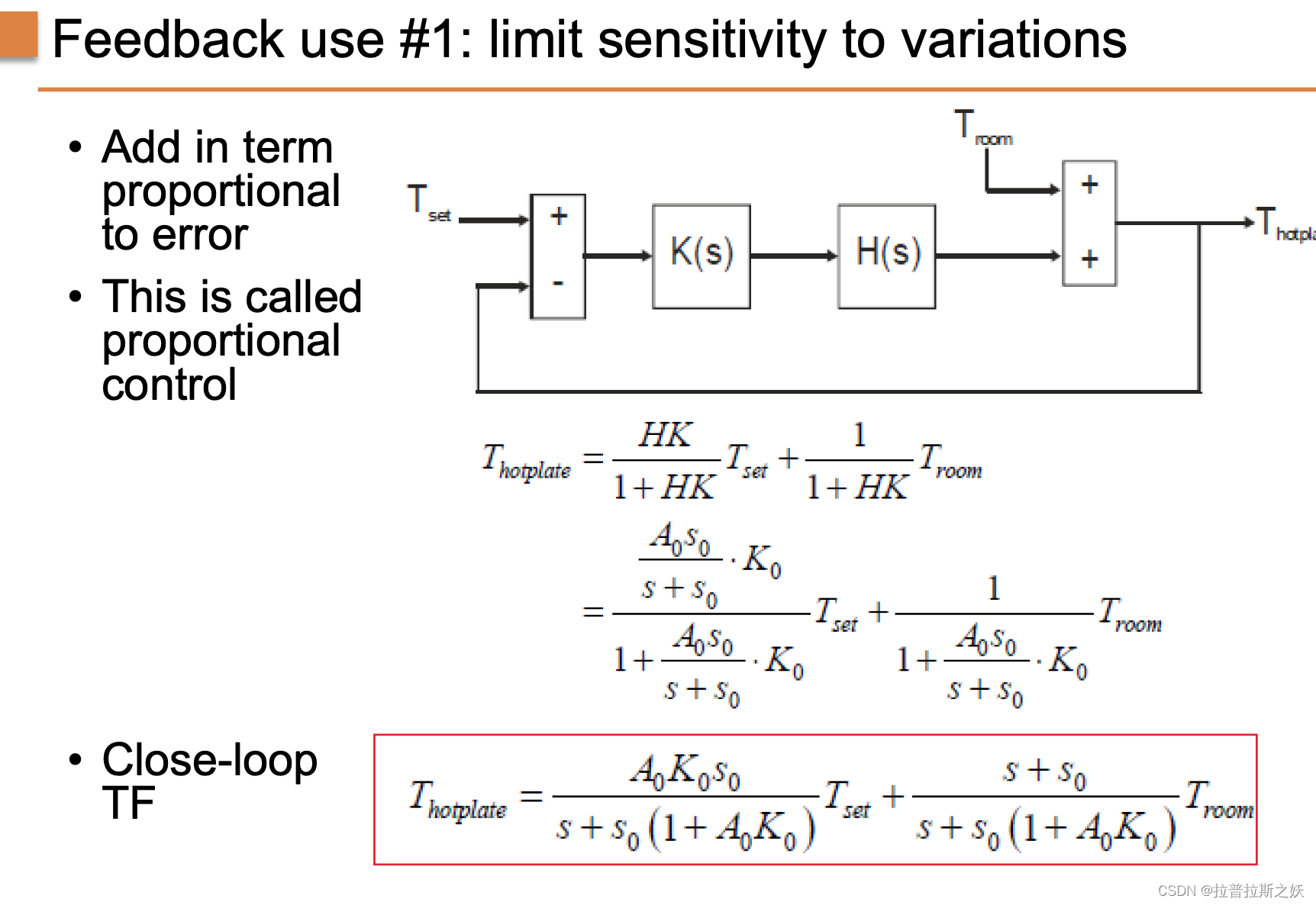
比例控制的基本思想是将误差（设定值与实际值之间的差异）按比例放大后作为控制输入的一部分。这可以通过以下公式表示：

$$T_{\text{hotplate}}=\frac{HK}{1+HK}{T}_{\text{set}}+\frac{1}{1+HK}{T}_{\text{room}}$$

其中：

• $H$ 和 $K$ 分别是系统的传递函数和控制器的增益。
• $T_{\text{set}}$ 是设定温度。
• $T_{\text{room}}$ 是环境温度。

通过代数变换，闭环传递函数可以表示为：

$$T_{\text{hotplate}}=\frac{A_0{s}_0{K}_0}{s+s_0(1+A_0{K}_0)}{T}_{\text{set}}+\frac{s+s_0}{s+s_0(1+A_0{K}_0)}{T}_{\text{room}}$$

闭环系统的优点

通过闭环控制，系统对外界变化的敏感性大大降低。图中的示意图展示了比例控制系统的框图：

• 设定点温度 $T_{\text{set}}$：用户设定的目标温度。
• 误差计算：设定点与实际温度之间的差值。
• 控制器 $K(s)$：根据误差生成控制信号。
• 执行机构 $H(s)$：实际调节温度的部分。

通过这种反馈机制，系统可以在面对环境温度变化或系统参数漂移时保持稳定的输出。

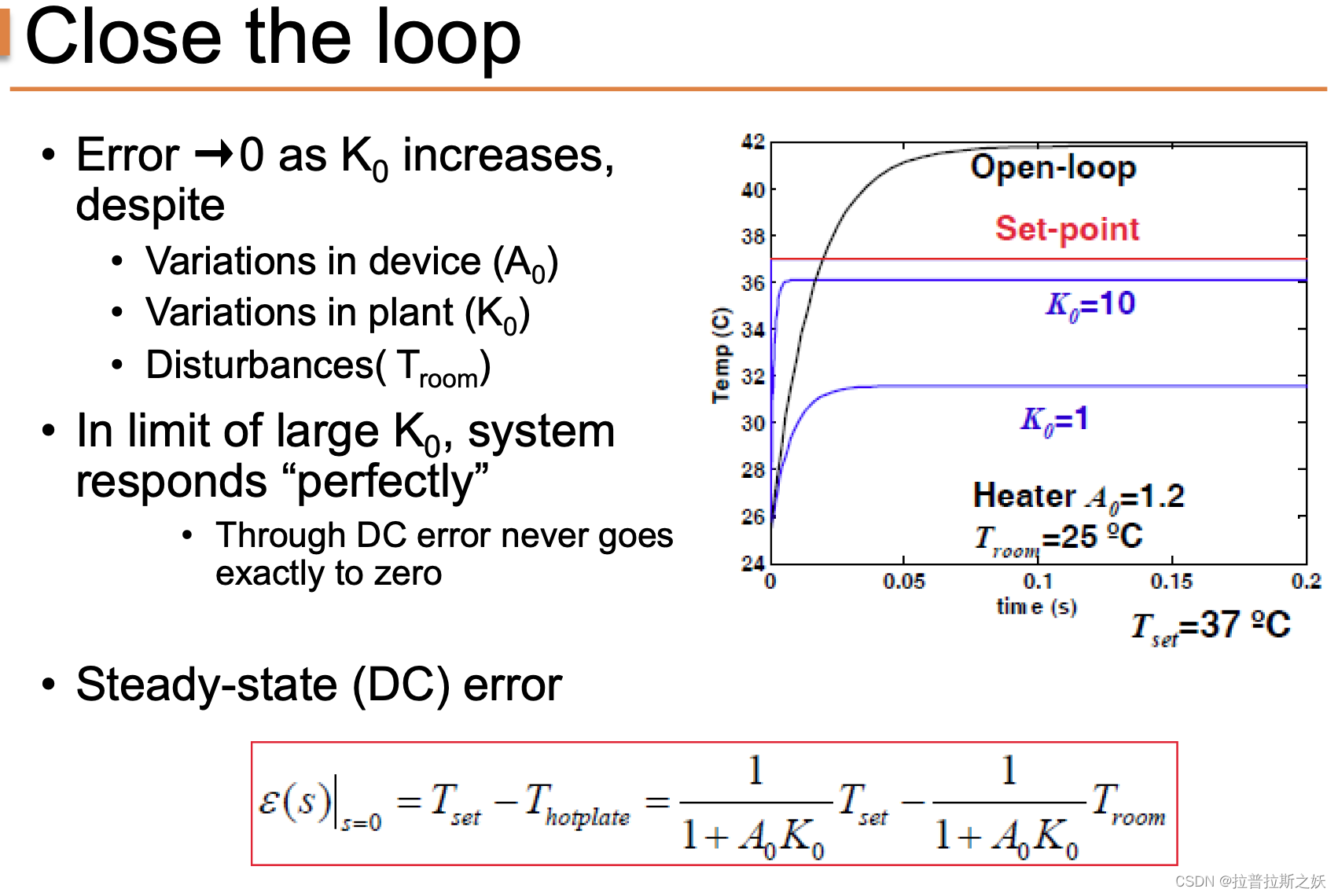
随着控制增益 $K_0$ 的增加，系统的误差逐渐减小，即使存在设备参数 $A_0$、执行机构特性 $K_0$ 和扰动（如环境温度 $T_{\text{room}}$）的变化。理论上，当 $K_0$ 足够大时，系统的响应将“完美”，尽管直流误差（DC error）永远不可能完全为零。

图中展示了不同增益下系统的温度响应：

• 开环系统：黑色曲线显示了开环系统的响应，未能达到设定温度。
• 闭环系统：蓝色和紫色曲线分别展示了增益 $K_0$ 为1和10时的闭环系统响应，显著改善了温度控制效果。

比例控制优点1：降低稳态误差

稳态误差是系统在达到稳定状态后的残余误差。对于比例控制系统，稳态误差可以表示为：

$$ϵ(s){|}_{s=0}=T_{\text{set}}-T_{\text{hotplate}}=\frac{1}{1+A_0{K}_0}{T}_{\text{set}}-\frac{1}{1+A_0{K}_0}{T}_{\text{room}}$$

这表明，随着 $K_0$ 的增加，稳态误差趋近于零。

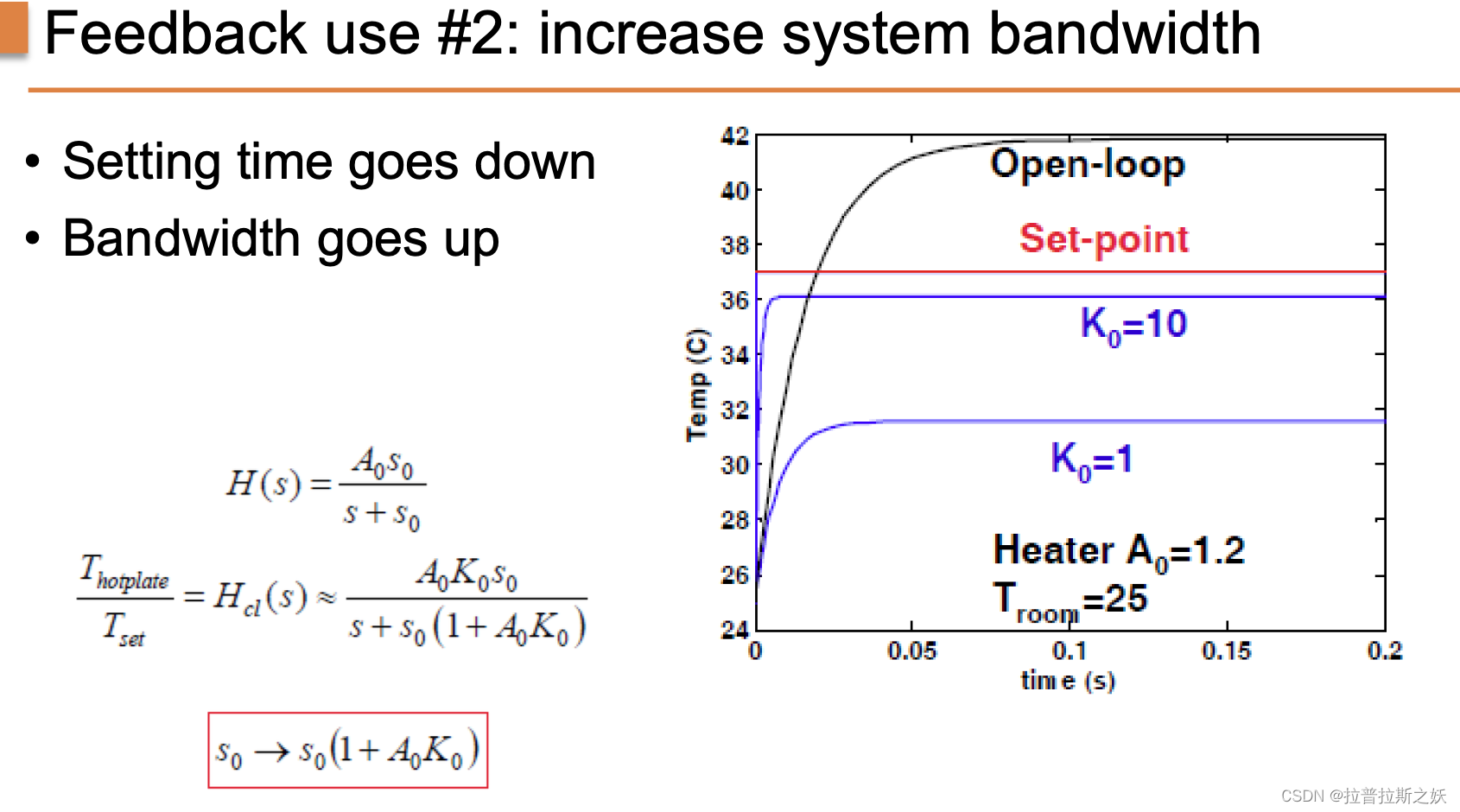
比例控制优点1：增加系统带宽

反馈控制的另一个主要用途是增加系统的带宽，从而加快系统的响应时间。带宽越高，系统的响应速度越快，能够更迅速地达到设定值。

通过增加控制器增益 $K_0$，系统的带宽也随之增加。系统的传递函数可以表示为：

$$H(s)=\frac{A_0{s}_0}{s+s_0}$$

闭环系统的传递函数则为：

$$\frac{T_{\text{hotplate}}}{T_{\text{set}}}=H_{cl}(s)\approx \frac{A_0{K}_0{s}_0}{s+s_0(1+A_0{K}_0)}$$

这表明，随着 $K_0$ 的增加，系统的极点 $s_0$ 向左移动，系统的响应速度加快，带宽增加。

图中展示了不同增益下系统的响应曲线：

• 开环系统：黑色曲线显示了开环系统的响应，响应时间较长。
• 闭环系统：蓝色和紫色曲线分别展示了增益 $K_0$ 为1和10时的闭环系统响应，显著减少了系统的响应时间。

二阶系统

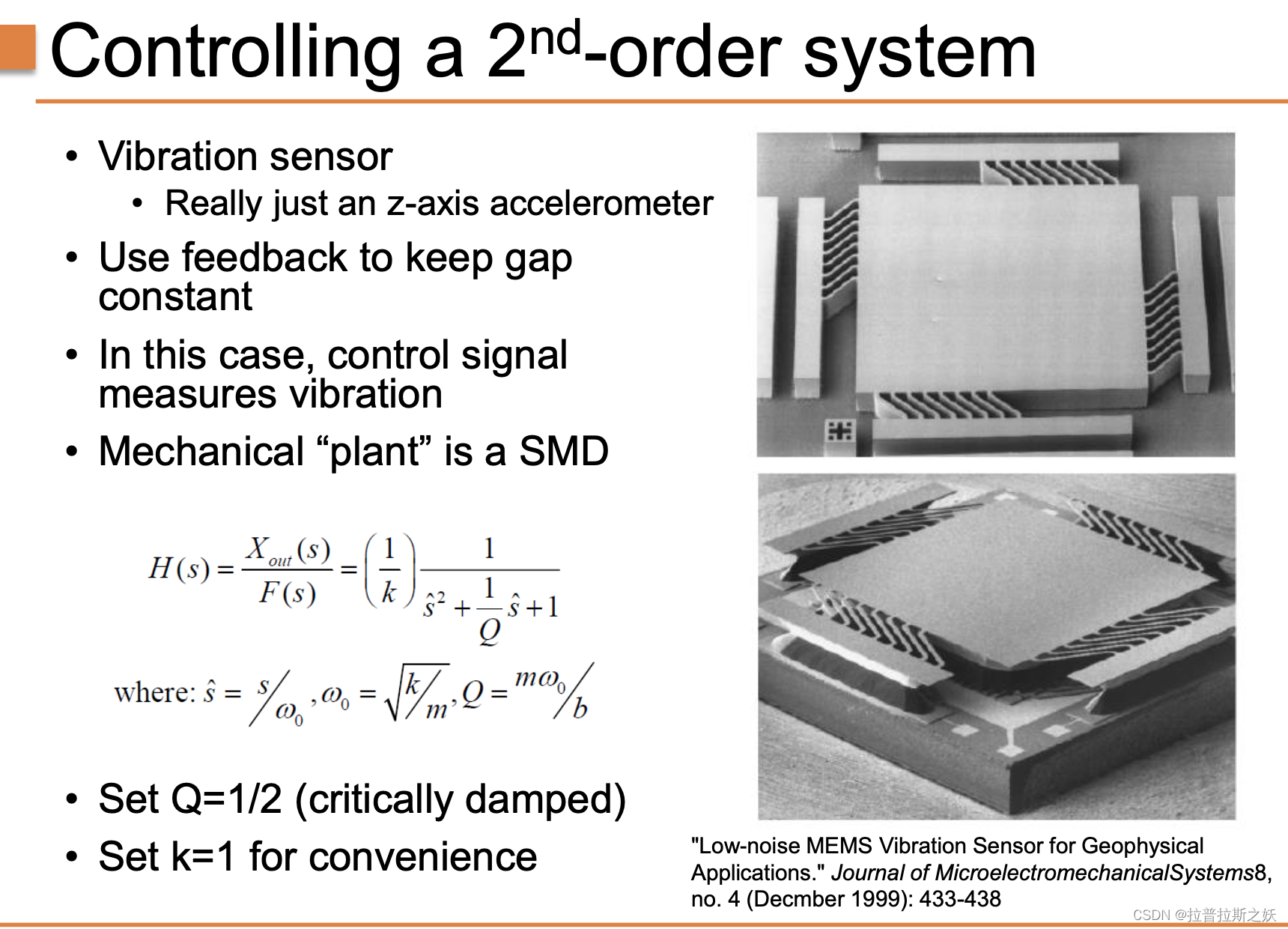
在控制系统中，二阶系统比一阶系统更复杂，通常用于描述振动传感器等具有弹簧和阻尼特性的机械系统。这里以振动传感器（实际上是一个z轴加速度计）为例，通过反馈控制保持间隙恒定，从而精确测量振动。

振动传感器和机械“植物”

振动传感器通过检测物体在z轴方向上的加速度来测量振动。反馈控制用于保持传感器和测量对象之间的间隙恒定，从而确保测量精度。在这种情况下，控制信号实际上测量的是振动。

机械“植物”（Plant）是一个简单的机械谐振系统（SMD），其传递函数 $H(s)$ 表示为：

$$H(s)=\frac{X_{\text{out}}(s)}{F(s)}=\frac{1}{k}\cdot \frac{1}{s^2+\frac{1}{Q}s+1}$$

其中：

• $k$ 是弹簧常数。
• $Q$ 是品质因数，表示系统的阻尼特性。
• ${\omega }_0$ 是系统的自然频率， ${\omega }_0=\sqrt{\frac{k}{m}}$。
• $\hat{s}=\frac{s}{{\omega }_0}$。

在实际设计中，通常将 $Q$ 设为 $\frac{1}{2}$（临界阻尼），以避免系统过度振荡，并将 $k$ 设为1以简化计算。

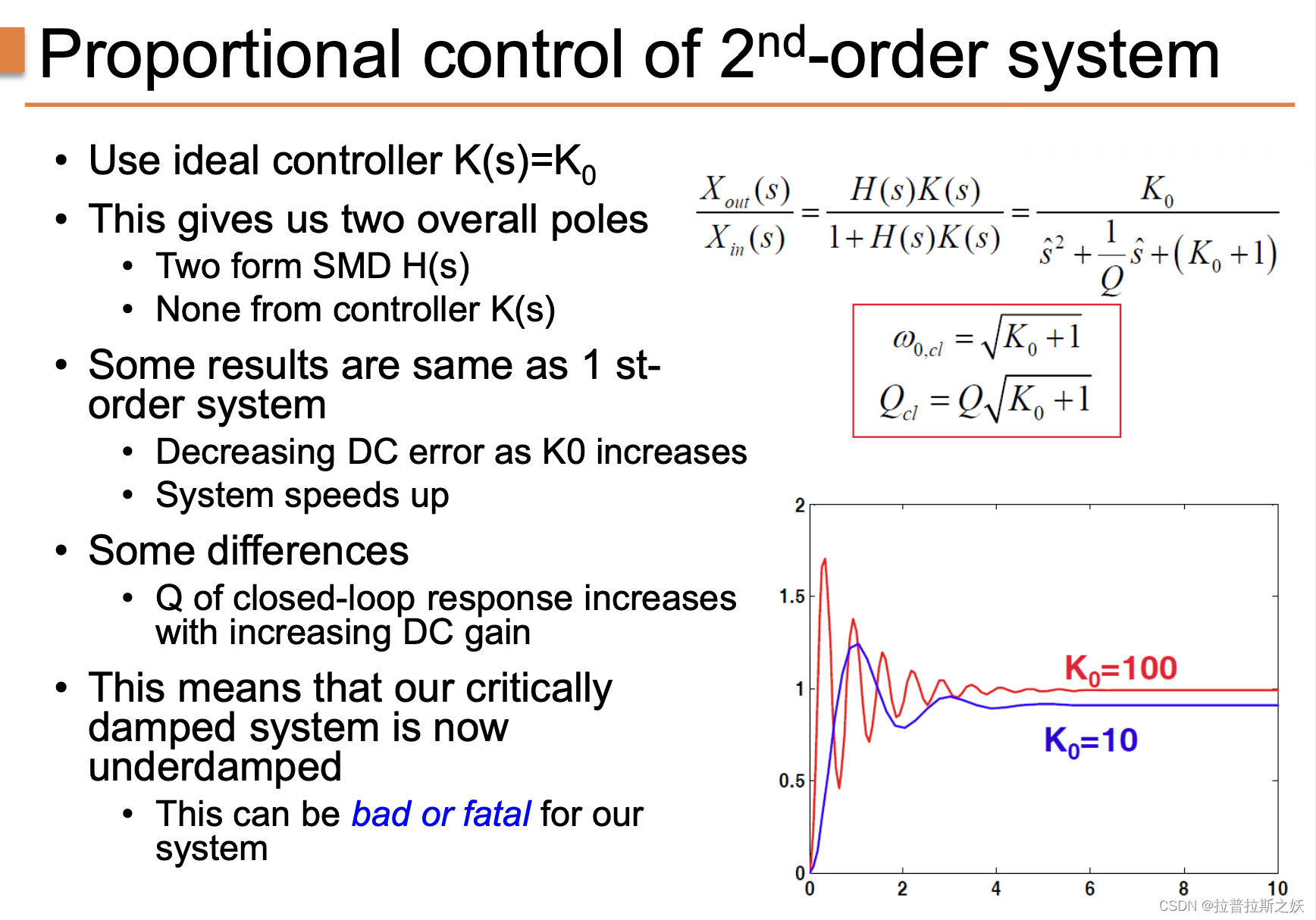
二阶系统的比例控制

比例控制是一种常见的控制方法，通过调整控制增益 $K_0$ 来调节系统的响应。在理想情况下，控制器 $K(s)=K_0$，则系统的闭环传递函数为：

$$\frac{X_{\text{out}}(s)}{X_{\text{in}}(s)}=\frac{H(s)K(s)}{1+H(s)K(s)}=\frac{K_0}{{\hat{s}}^2+\frac{1}{Q}\hat{s}+(K_0+1)}$$

这表明闭环系统有两个极点（由SMD $H(s)$ 决定），控制器本身没有引入新的极点。系统的自然频率和品质因数分别为：

$${\omega }_{0,\text{cl}}=\sqrt{K_0+1}$$
$$Q_{\text{cl}}=Q\sqrt{K_0+1}$$

控制效果分析

图中展示了不同控制增益下二阶系统的响应曲线：

• 增益 $K_0=10$：蓝色曲线显示系统响应较快，且阻尼效果良好。
• 增益 $K_0=100$：红色曲线显示系统响应速度更快，但由于品质因数 $Q$ 增加，系统变为欠阻尼，产生明显的振荡。

随着 $K_0$ 的增加，系统的DC误差减少，响应速度加快。然而，增益过大会导致系统品质因数 $Q$ 增加，使得临界阻尼系统变为欠阻尼系统，这对系统的稳定性和控制精度不利，甚至可能导致系统失效。

复杂系统的控制

在控制工程中，复杂系统的动态行为通常由其闭环系统的传递函数 $H(s)K(s)$ 决定。这意味着，二阶系统的行为不仅取决于系统本身的动态特性，还与控制器的设计密切相关。通过将不同的控制器与系统耦合，可以观察到系统的不同行为。

一阶系统与二阶系统的相似性

例如，一阶热系统（thermal system）与一阶控制器的耦合，其行为可以类比于二阶SMD系统。这是因为系统的总响应不仅取决于单个元素的特性，还受到系统整体配置的影响。

当在系统中增加额外的极点时，系统的复杂性显著增加。以下是对这种情况的详细分析：

单极点控制器（真实放大器）

如果将SMD系统与一阶控制器耦合，系统将包含三个极点。传递函数 $K(s)$ 可以表示为：

$$K(s)=\frac{K_0}{1+\hat{s}\tau }$$

其中， $\hat{s}={\omega }_0\tau$ 为控制器时间常数。这样，系统的闭环传递函数变为：

$$\frac{X_{\text{out}}(s)}{X_{\text{in}}(s)}=\frac{K_0}{{\hat{s}}^3+(1+2\hat{\tau }){\hat{s}}^2+(2+\hat{\tau })\hat{s}+K_0+1}$$

稳定性分析

随着 $K_0$ 的增加，系统可能变得不稳定。这种不稳定性发生在闭环系统的一个根具有正的实部时。通过Routh稳定性判据，可以确定系统稳定性的条件：

对于三阶系统，其特征方程为：

$$a_3{s}^3+a_2{s}^2+a_{1}s+a_0$$

Routh判据要求所有系数 $a_n$ 具有相同符号，并且满足：

$$a_2{a}_1>a_0{a}_3$$

这意味着，控制增益 $K_0$ 的上限可以表示为：

$$K_0<\frac{1}{Q}\left(\frac{1}{Q}+\hat{\tau }+\frac{1}{\hat{\tau }}\right)$$

二阶系统与三阶系统的对比

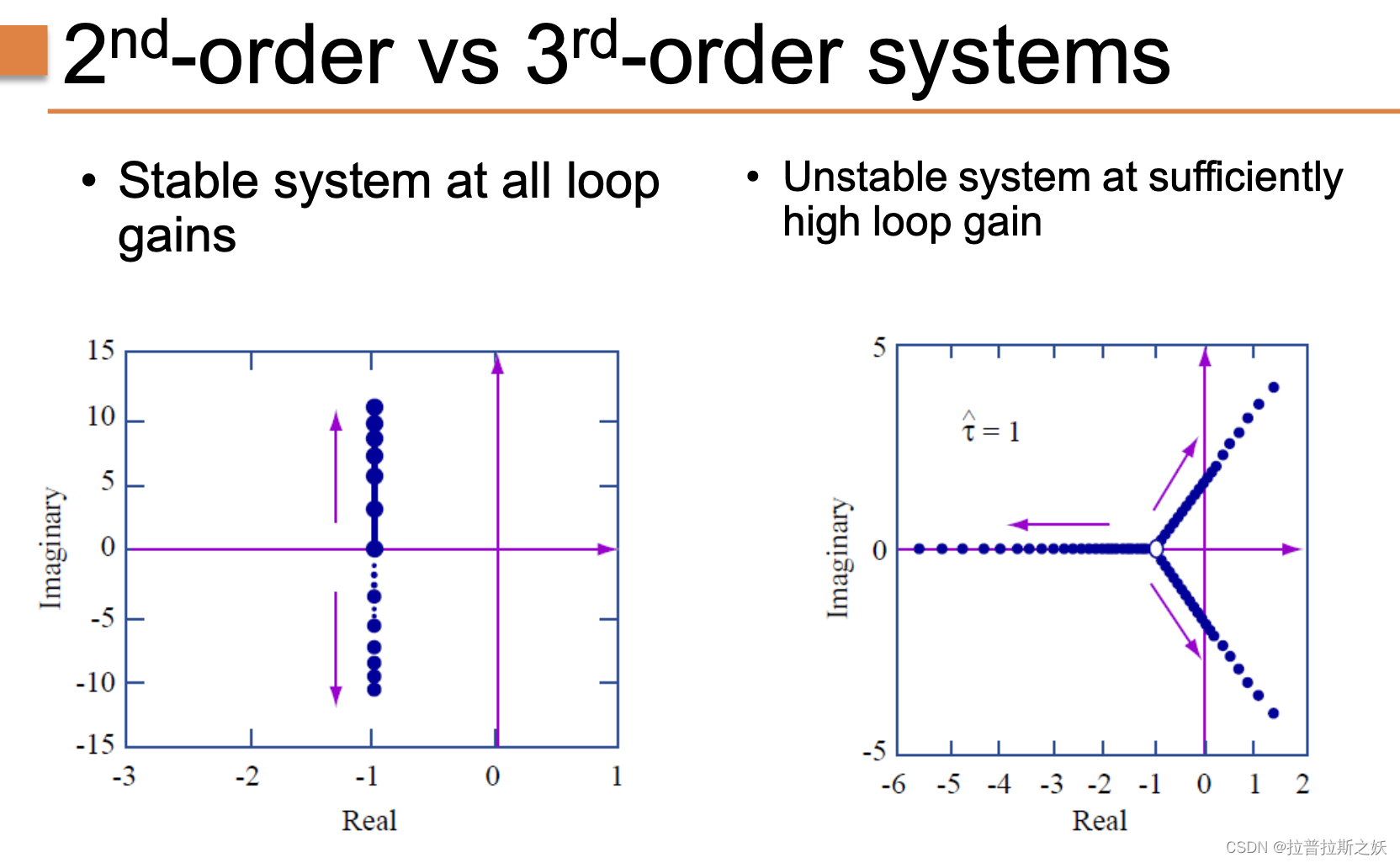
如图所示，二阶系统在所有环路增益下都是稳定的。然而，三阶系统在环路增益足够高时可能变得不稳定。

• 二阶系统：所有极点在复平面左半部分，系统稳定。
• 三阶系统：当环路增益增加时，系统的极点可能移至右半平面，导致不稳定。

通过极点图可以直观地观察到这种变化。二阶系统的极点随着增益变化在实轴上移动，而三阶系统的极点可能离开实轴，进入右半平面。

控制器带宽的影响

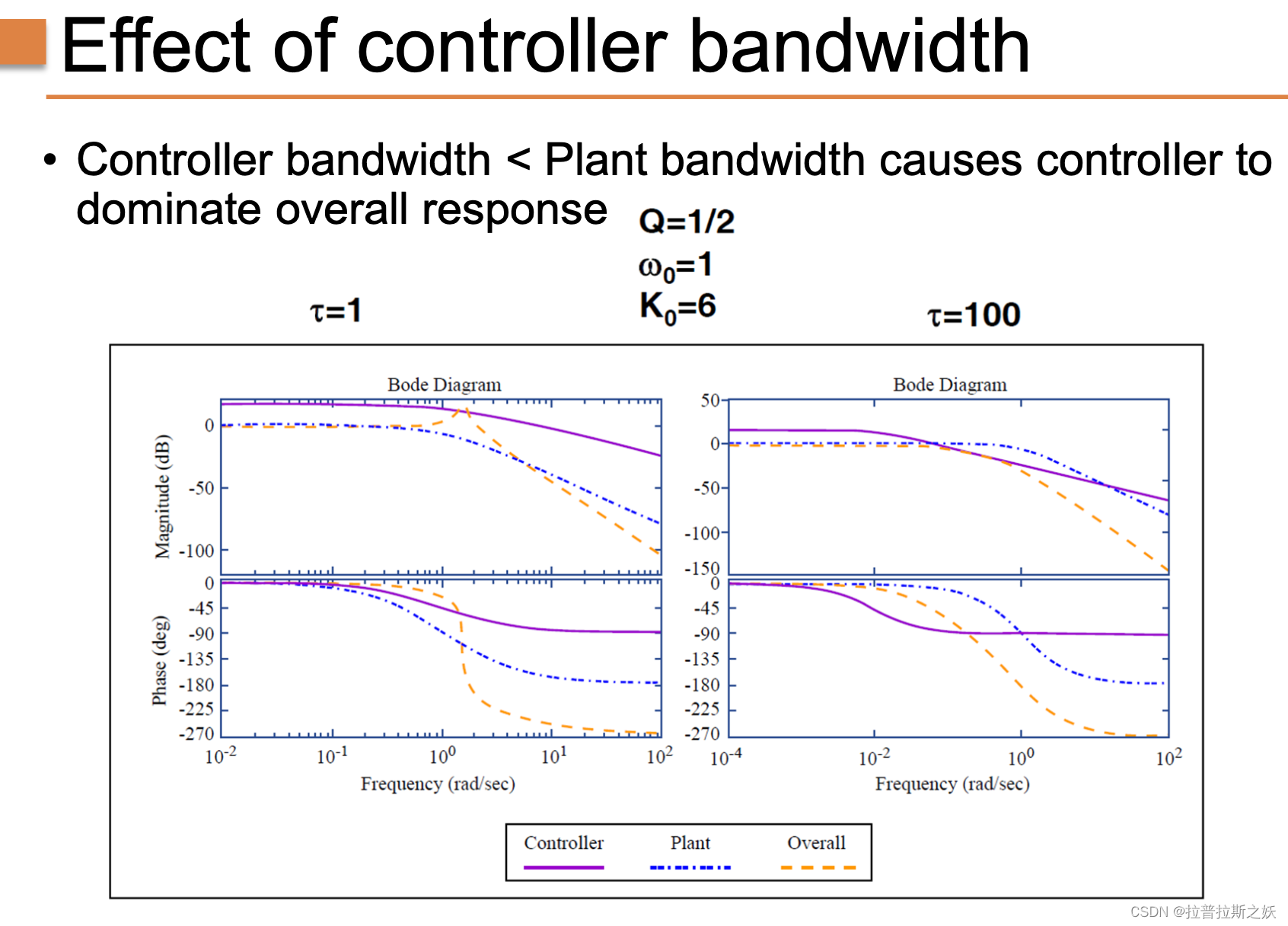
控制器带宽是指控制器能够有效调节的频率范围。在控制系统设计中，控制器的带宽相对于系统（即植物）的带宽至关重要。当控制器的带宽低于植物的带宽时，控制器将主导系统的整体响应，这可能导致控制性能不佳。

图中展示了不同时间常数 $\tau$ 下系统的Bode图：

• 左图（ $\tau =1$）：控制器的带宽与植物的带宽相当，整体响应由两者共同决定。
• 右图（ $\tau =100$）：控制器的带宽远小于植物的带宽，控制器主导整体响应，导致系统的相位和增益显著变化。

在这两种情况下，控制器的传递函数和植物的传递函数共同决定了系统的频率响应特性。通常，设计控制系统时，希望控制器的带宽与植物的带宽相匹配，以实现更好的控制性能。

PI控制（比例-积分控制）

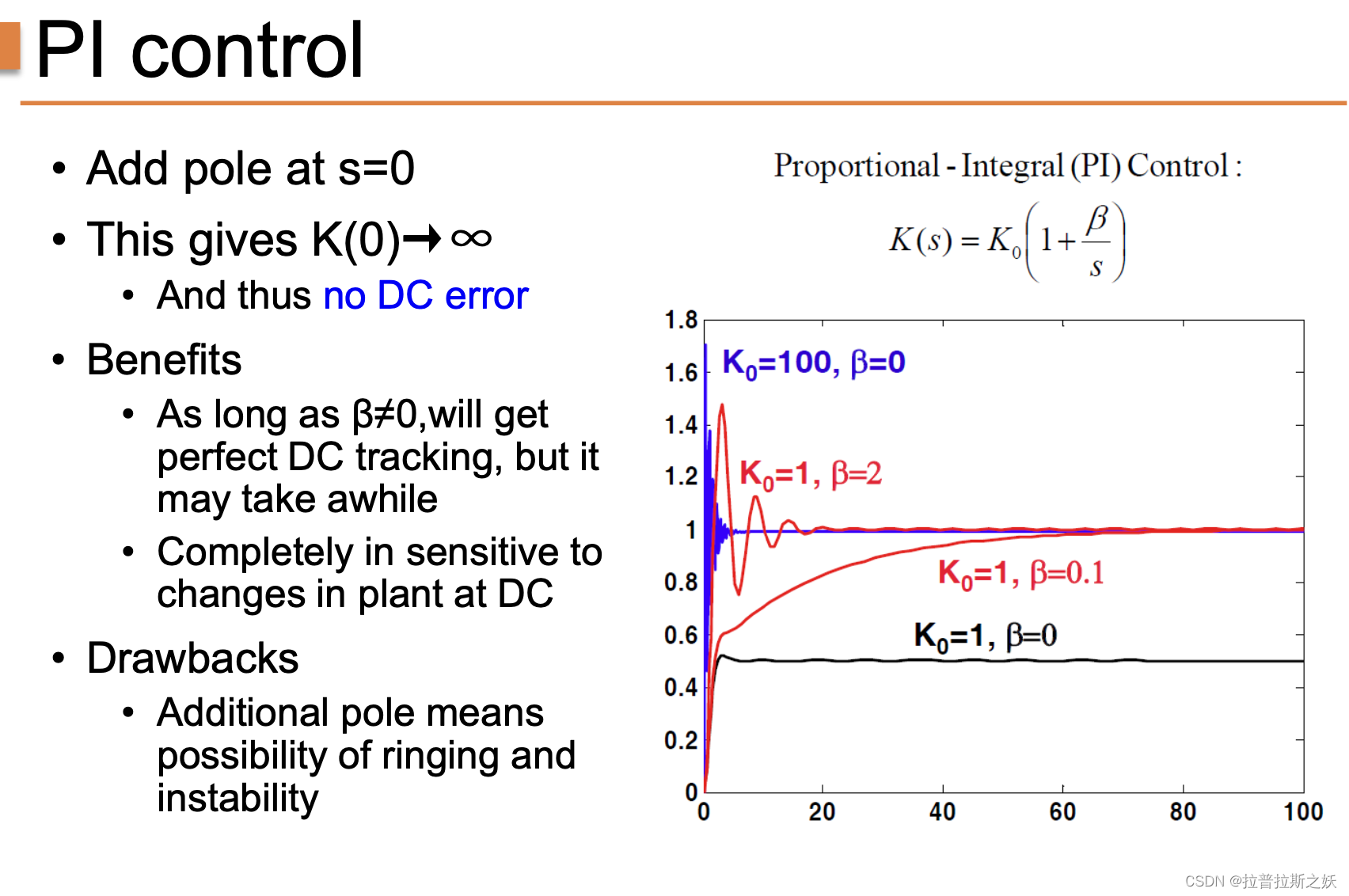
PI控制是通过在控制器中添加一个积分项来消除稳态误差。积分项的引入使得控制器在直流（DC）下具有无限增益，从而能够实现零稳态误差。

PI控制的优点在于其能够完全消除稳态误差，并对植物参数的变化不敏感。然而，积分项的引入也可能导致系统产生振铃和不稳定性，特别是在高增益情况下。

PI控制器的传递函数为：

$$K(s)=K_0\left(1+\frac{\beta }{s}\right)$$

其中：

• $K_0$ 是比例增益。
• $\beta$ 是积分增益，决定了积分项的强度。

图中展示了不同参数下PI控制系统的响应曲线：

• ** $K_0=100,\beta =0$**：没有积分作用，系统快速响应但存在稳态误差。
• ** $K_0=1,\beta =2$**：积分项显著，系统在消除稳态误差的同时引入了明显的振荡。
• ** $K_0=1,\beta =0.1$**：较弱的积分作用，系统响应较为平稳。

PID控制（比例-积分-微分控制）

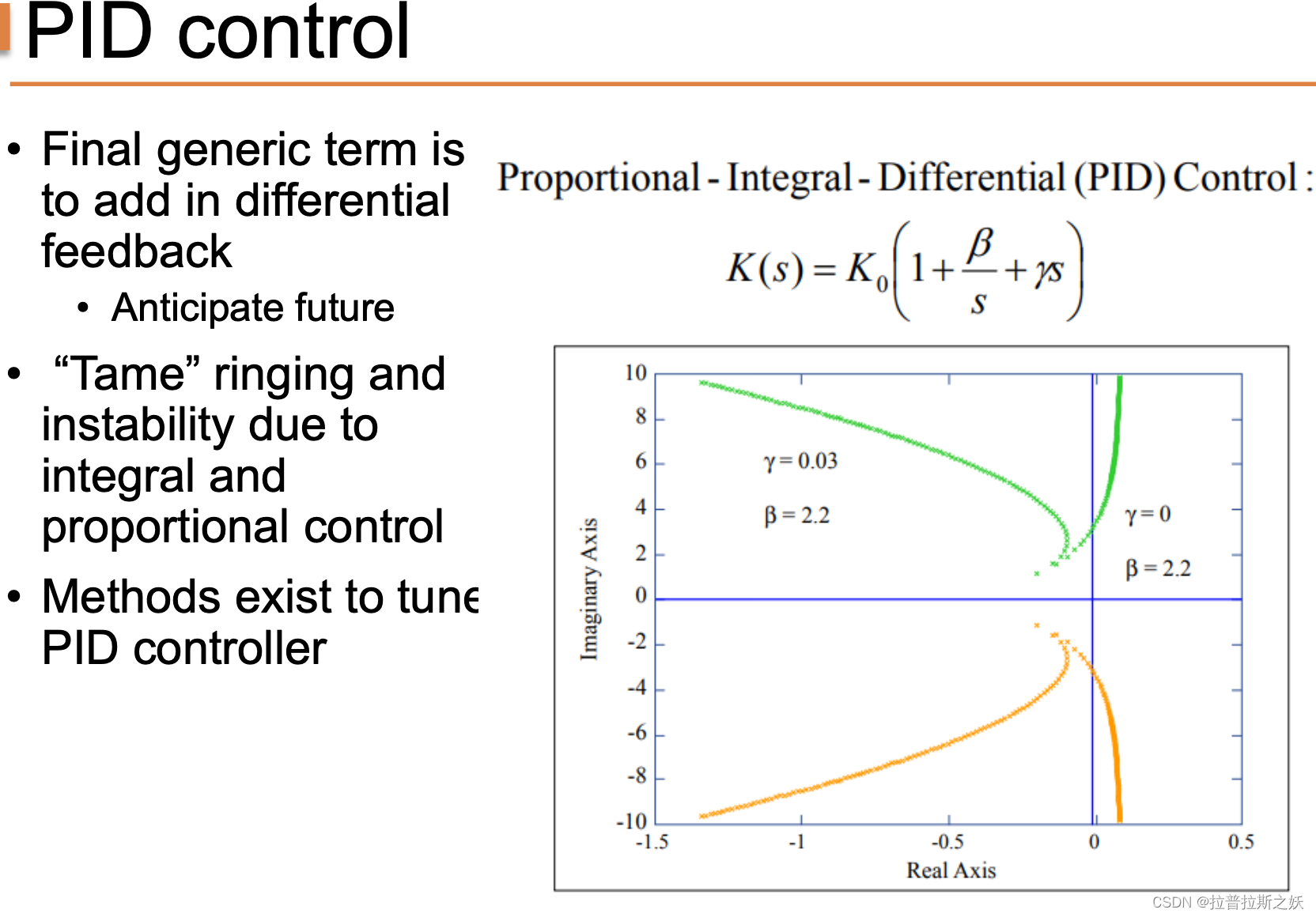
PID控制通过在控制器中添加微分项，进一步改进系统的动态性能。微分项能够预见未来的误差变化，从而提前进行调节，抑制积分项引入的振铃和不稳定性。

PID控制器的传递函数为：

$$K(s)=K_0\left(1+\frac{\beta }{s}+\gamma s\right)$$

其中：

• $\gamma$ 是微分增益，决定了微分项的强度。

图中展示了不同参数下PID控制系统的根轨迹图：

• ** $\gamma =0.03,\beta =2.2$**：系统具有较强的微分作用，响应快速且稳定。
• ** $\gamma =0,\beta =2.2$**：没有微分作用，系统可能出现振铃和不稳定性。

PID控制结合了比例、积分和微分三种控制方式，能够在不同频率范围内优化系统的响应。然而，PID控制器的参数调节较为复杂，需要通过试验或优化算法进行调整，以获得最佳性能。

不稳定系统的稳定化

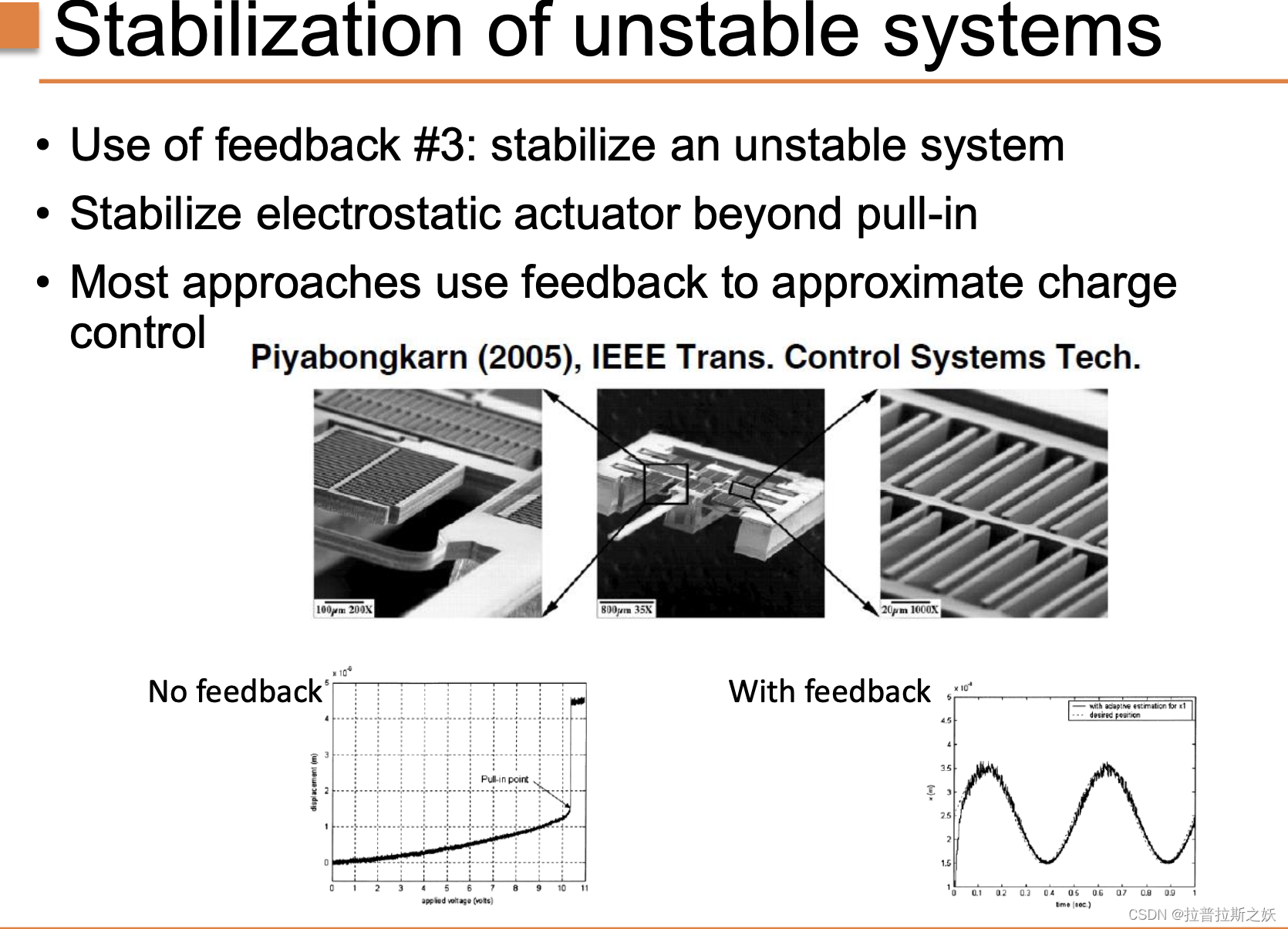
反馈控制的一个重要用途是稳定本质上不稳定的系统。通过适当的反馈机制，可以将系统从不稳定状态拉回到稳定状态。这在电静电执行器等应用中尤为重要。

电静电执行器的稳定化

电静电执行器在拉入点（pull-in point）后会变得不稳定，即当施加电压超过某一临界值时，执行器会迅速吸引到电极上，导致失控。通过反馈控制，可以在超越拉入点后保持系统的稳定。

图中展示了一种利用反馈控制实现电静电执行器稳定化的方法：

• 无反馈（No feedback）：系统在拉入点后变得不稳定。
• 有反馈（With feedback）：通过反馈控制，系统在拉入点后仍然保持稳定。

这种方法通常通过反馈近似控制电荷，从而实现系统的稳定性。

可观测性和可控性

为了稳定潜在的不稳定模式，系统必须既可观测又可控：

• 可观测性（Observable）：意味着传感器能够提供关于模式状态的信息。如果系统的某个模式无法通过传感器观测到，那么无法对其进行有效控制。
• 可控性（Controllable）：意味着控制输入可以修改该模式。如果模式无法被控制输入影响，那么即使观测到该模式，也无法实现控制。

如果一个模式同时具有可观测性和可控性，则理论上可以通过反馈实现稳定。

增加传感器和执行器

通过增加传感器，可以提高系统模式的可观测性，使更多的模式可以被监测和控制。增加执行器则可以提高系统模式的可控性，使控制输入可以更有效地调节系统。

从不稳定到不受欢迎的模式

除了稳定不稳定的模式，反馈控制还可以用于抑制不受欢迎的模式。例如，在机械系统中，一些振动模式可能是不希望出现的，通过反馈控制可以抑制这些振动，提高系统的性能和寿命。

案例研究

参考图中展示的Piyabongkarn（2005）在IEEE控制系统技术上的研究，展示了电静电执行器在有无反馈控制情况下的不同表现：

• 没有反馈：施加电压超过某个值后，执行器进入不稳定状态，无法继续工作。
• 有反馈：通过反馈控制，系统在高电压下仍然保持稳定，执行器能够正常运行。

这种研究展示了反馈控制在实际工程应用中的重要性和有效性。

反馈控制是稳定不稳定系统的关键技术，通过适当的反馈机制，可以将系统从不稳定状态拉回到稳定状态。确保系统的模式可观测和可控是实现这一目标的前提。增加传感器和执行器可以提高系统的可观测性和可控性，从而更好地实现系统的稳定化。在实际应用中，反馈控制不仅可以用于稳定不稳定系统，还可以用于抑制不受欢迎的模式，提高系统的性能和寿命。

MEMS控制

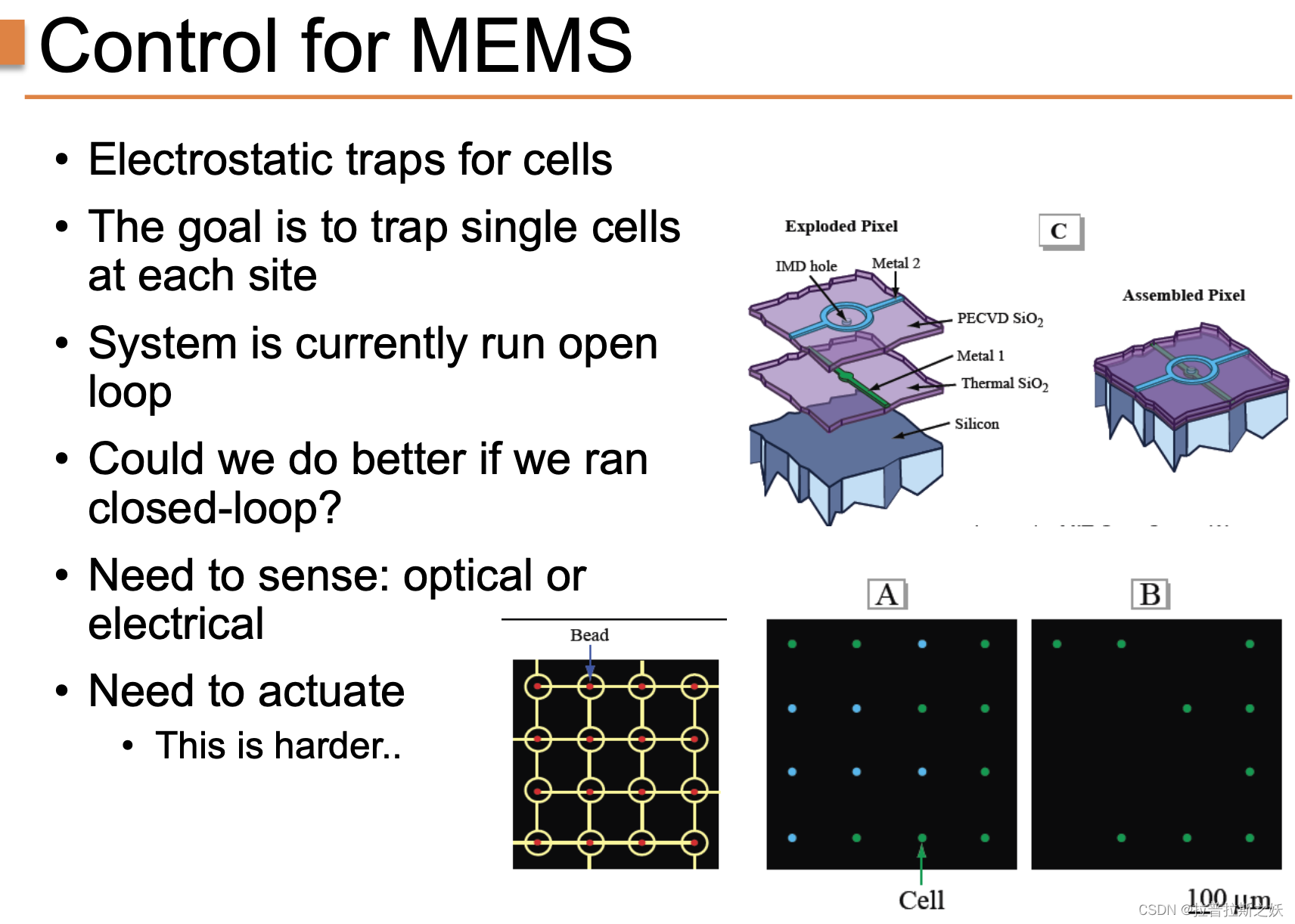
微机电系统（MEMS）在微观尺度上实现了复杂的机械和电气功能，在生物医学领域有广泛的应用，例如细胞的电静电捕获。这张幻灯片展示了一个MEMS系统用于捕获单个细胞的示例。

电静电捕获细胞

电静电捕获是一种通过静电力将细胞固定在特定位置的方法。这种技术常用于单细胞分析和处理，目标是在每个捕获位置捕获单个细胞。

1. 目前系统是开环运行的：

   • 开环系统不使用反馈控制，依赖于预设的电压或电流来捕获细胞。
   • 缺点是对外界变化（如环境温度、细胞大小变化等）缺乏适应能力，捕获效率和精度可能较低。

2. 闭环控制的潜力：

   • 问题提出：如果系统采用闭环控制，性能是否会更好？
   • 闭环控制通过实时监测和调整，能够提高系统的鲁棒性和精度。
   • 需要传感：通过光学或电气方式实时监测细胞的位置。
   • 需要执行：精确控制电压或电流，调整捕获力。

系统结构和工作原理

幻灯片中的示意图展示了MEMS系统的结构：

• Exploded Pixel（展开像素）：

  • 由多个层次组成，包括PECVD SiO2、Metal 1、Metal 2等。
  • 每层具有特定功能，如导电、绝缘等。
  • 硅基底提供机械支撑。

• Assembled Pixel（组装像素）：

  • 完整的像素单元，用于实际的细胞捕获。
  • 通过电压控制，实现静电力场的产生。

• 捕获阵列示意图：

  • 左图（A）：显示了没有细胞的捕获阵列，每个捕获位置为空。
  • 右图（B）：显示了捕获单个细胞的阵列，每个位置成功捕获一个细胞，间距为100微米。

闭环控制的实现

为了实现闭环控制，需要解决以下关键问题：

1. 传感器的选择：

   • 光学传感：使用显微镜或CCD相机实时监测细胞位置。
   • 电气传感：使用电容或阻抗变化来检测细胞的存在和位置。

2. 执行机构的控制：

   • 精确控制电压或电流以调整静电力场。
   • 挑战在于快速响应和高精度控制，以适应细胞的快速运动和微小位移。

3. 控制算法：

   • 采用PID或更复杂的自适应控制算法，实现实时调整。
   • 控制系统需要具备抗干扰能力和高鲁棒性。

非线性系统中的反馈控制

非线性系统中，传统的代数形式往往无法有效描述系统的行为。然而，反馈控制的基本思想仍然适用，即通过预失真控制信号来补偿系统的非线性特性，从而实现期望的控制效果。

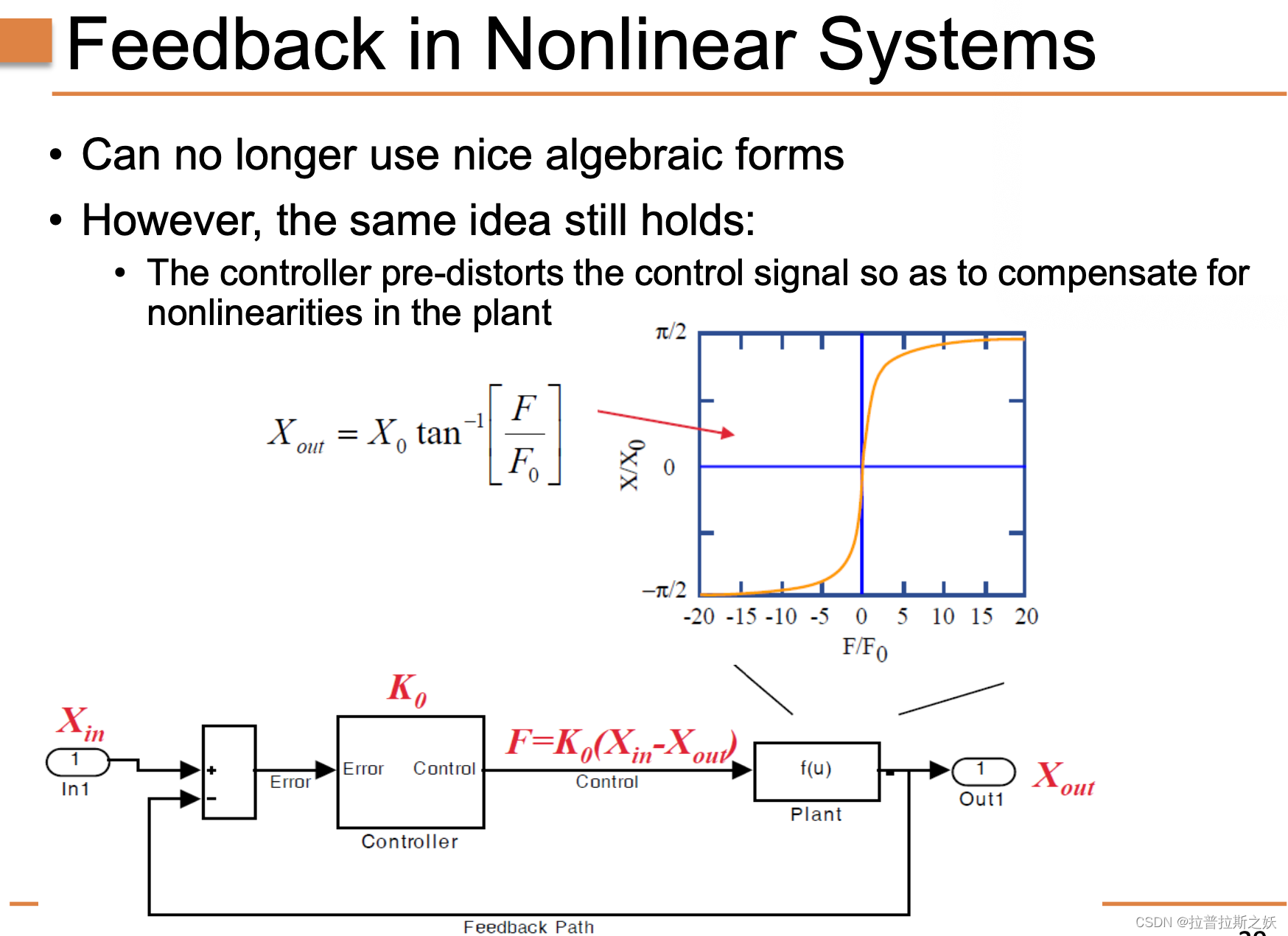
基本原理

对于非线性系统，控制器通过调整控制信号 $F$，使输出 $X_{\text{out}}$ 满足特定的非线性关系。系统的非线性特性可以表示为：

$$X_{\text{out}}=X_0{\tan }^{-1}\left(\frac{F}{F_0}\right)$$

其中：

• $X_0$ 和 $F_0$ 是系统的常数参数。
• ${\tan }^{-1}$ 表示反正切函数，描述了非线性的输入输出关系。

右上图显示了这一非线性关系的图形表示，其中 $X_{\text{out}}$ 对应于 $\frac{F}{F_0}$ 的反正切值。

反馈控制结构

反馈控制系统的结构如下图所示：

1. 误差计算：

   • 通过比较设定输入 $X_{\text{in}}$ 和实际输出 $X_{\text{out}}$，得到误差信号。

2. 控制器：

   • 控制器根据误差信号计算控制量 $F$，并预失真控制信号以补偿系统的非线性。

3. 非线性植物：

   • 非线性函数 $f(u)$ 描述了系统的非线性行为，输出 $X_{\text{out}}$ 由控制量 $F$ 和非线性函数 $f(u)$ 决定。

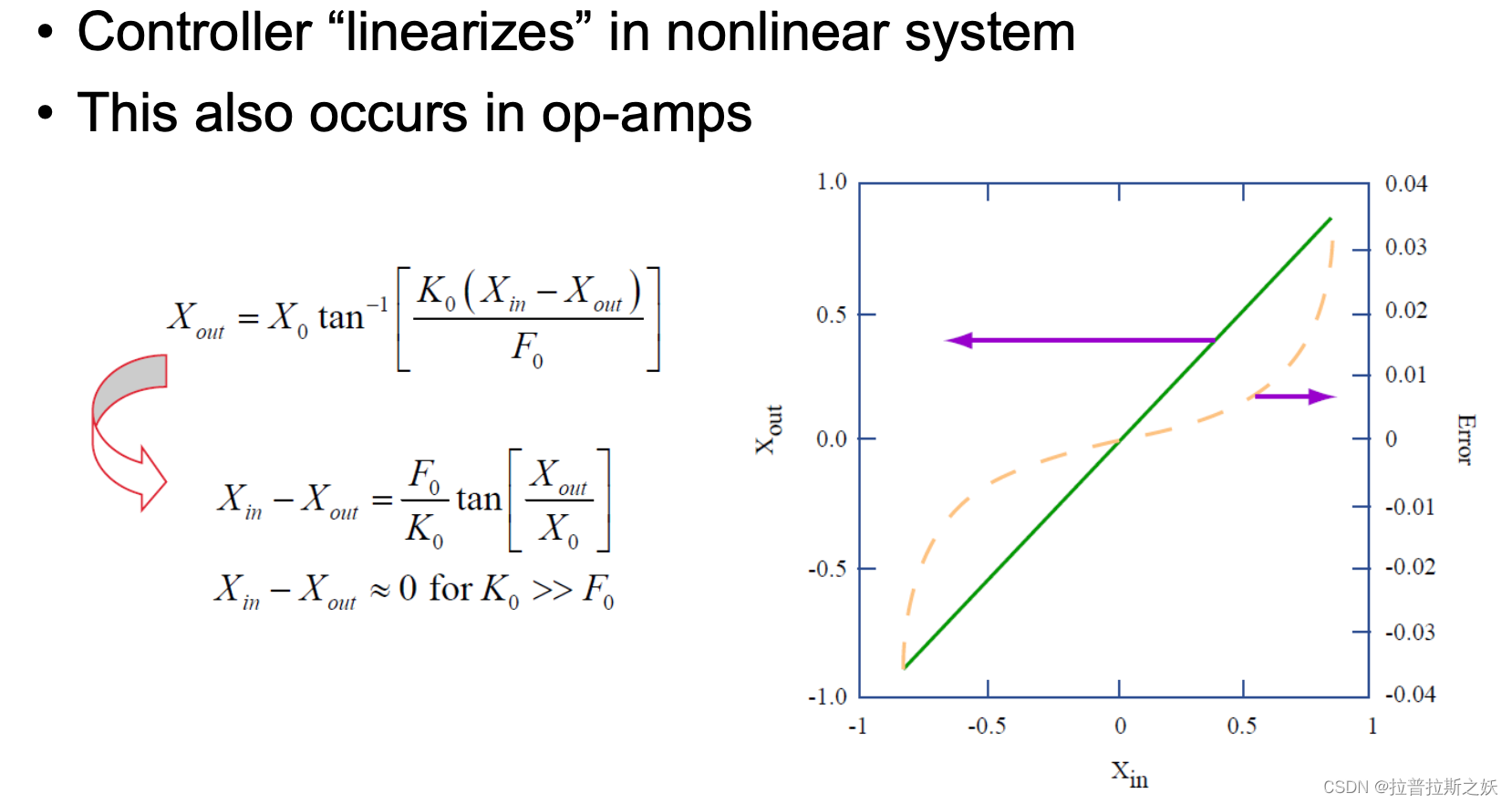
非线性系统的线性化

控制器可以通过预失真控制信号，使得非线性系统在一定范围内表现出线性行为。数学上，非线性系统的控制可以表示为：

$$X_{\text{out}}=X_0{\tan }^{-1}\left(\frac{K_0(X_{\text{in}}-X_{\text{out}})}{F_0}\right)$$

对上式进行变换，可以得到：

$$X_{\text{in}}-X_{\text{out}}=\frac{F_0}{K_0}\tan \left(\frac{X_{\text{out}}}{X_0}\right)$$

当控制器增益 $K_0$ 远大于系统常数 $F_0$ 时，误差 $X_{\text{in}}-X_{\text{out}}$ 接近于零，系统表现出近似线性行为。这意味着控制器有效地“线性化”了非线性系统，使得系统在较宽的范围内具有线性响应特性。

谐振器、振荡器和极限环

理解谐振器、振荡器和极限环在控制系统和信号处理中的角色，对于设计和分析复杂动态系统至关重要。谐振器提供了振荡的基础，振荡器通过主动增益元件实现持续振荡，而非线性元件则确保系统在安全范围内稳定工作。极限环作为非线性系统中的稳定周期性行为，对分析系统的长时间动态特性具有重要意义。

谐振器（Resonator）

• 定义：谐振器是一种被动元件，它在欠阻尼条件下表现出振荡行为。
• 特点：谐振器本身不具有能量增益功能，只能在特定频率下因外部激励而发生共振。这种共振会逐渐衰减，除非有持续的能量输入。

振荡器（Oscillator）

• 定义：振荡器是由谐振器加上一个主动增益元件组成的系统，能够补偿谐振器的损耗，产生稳定的振荡行为。
• 特点：振荡器不仅包括谐振元件，还集成了能够提供能量增益的主动元件。通过这种配置，振荡器能够维持持续的周期性振荡，是时钟、信号发生器等应用的核心组件。

限幅（Limiting）

• 定义：限幅是指在谐振器或增益元件中引入必要的非线性特性。
• 作用：这种非线性特性可以防止系统中的无限增益或振荡幅度增加，确保振荡器在一定范围内稳定工作。非线性特性通常通过设计在电路或控制算法中引入，以实现振荡幅度的限制和稳定。

极限环（Limit Cycle）

• 定义：极限环是状态空间中的稳定闭合路径。
• 特点：极限环代表系统在非线性条件下的稳定周期性运动。这种现象在非线性动力系统中非常常见，系统的状态会围绕极限环进行周期性运动，而不会趋向于一个固定点或发散。

图示解释

幻灯片的图示部分通过状态空间中的极限环、振荡器和谐振器的定义和行为，展示了这些概念的具体表现：

1. 谐振器（Resonator）：

   • 在无增益元件的情况下，只能通过外部能量维持振荡。
   • 欠阻尼时表现出短暂的振荡行为，随后逐渐衰减。

2. 振荡器（Oscillator）：

   • 包含主动增益元件，可以持续补偿谐振器的损耗。
   • 通过反馈和能量增益，实现持续的周期性振荡。

3. 限幅（Limiting）：

   • 通过引入非线性元件，限制振荡幅度，防止系统发散。
   • 确保振荡器在预定范围内稳定运行。

4. 极限环（Limit Cycle）：

   • 在状态空间中表现为稳定的闭合轨迹。
   • 系统在极限环上进行稳定的周期性运动，不会发散或趋向静止。

示例：谐振 RLC 电路

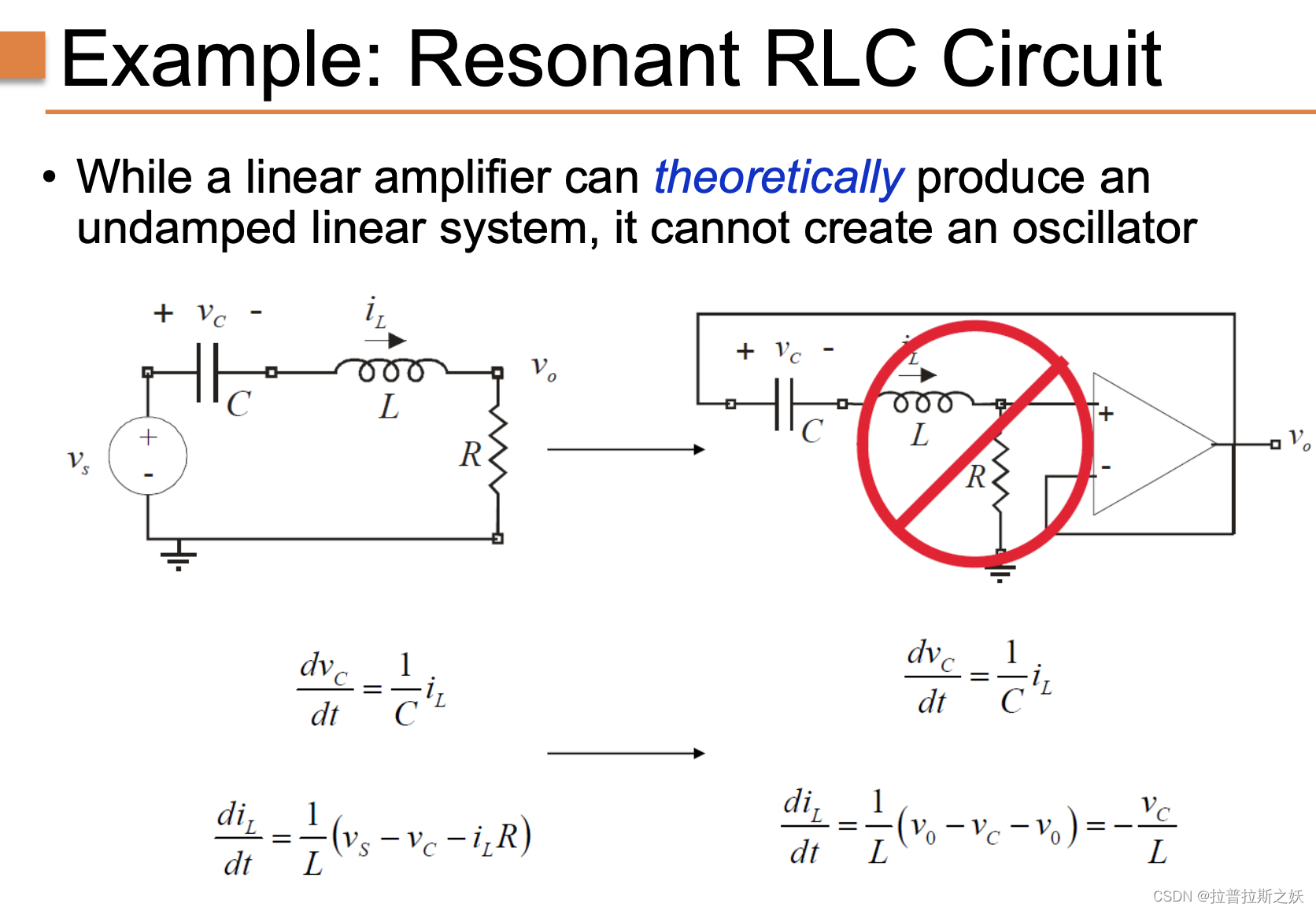
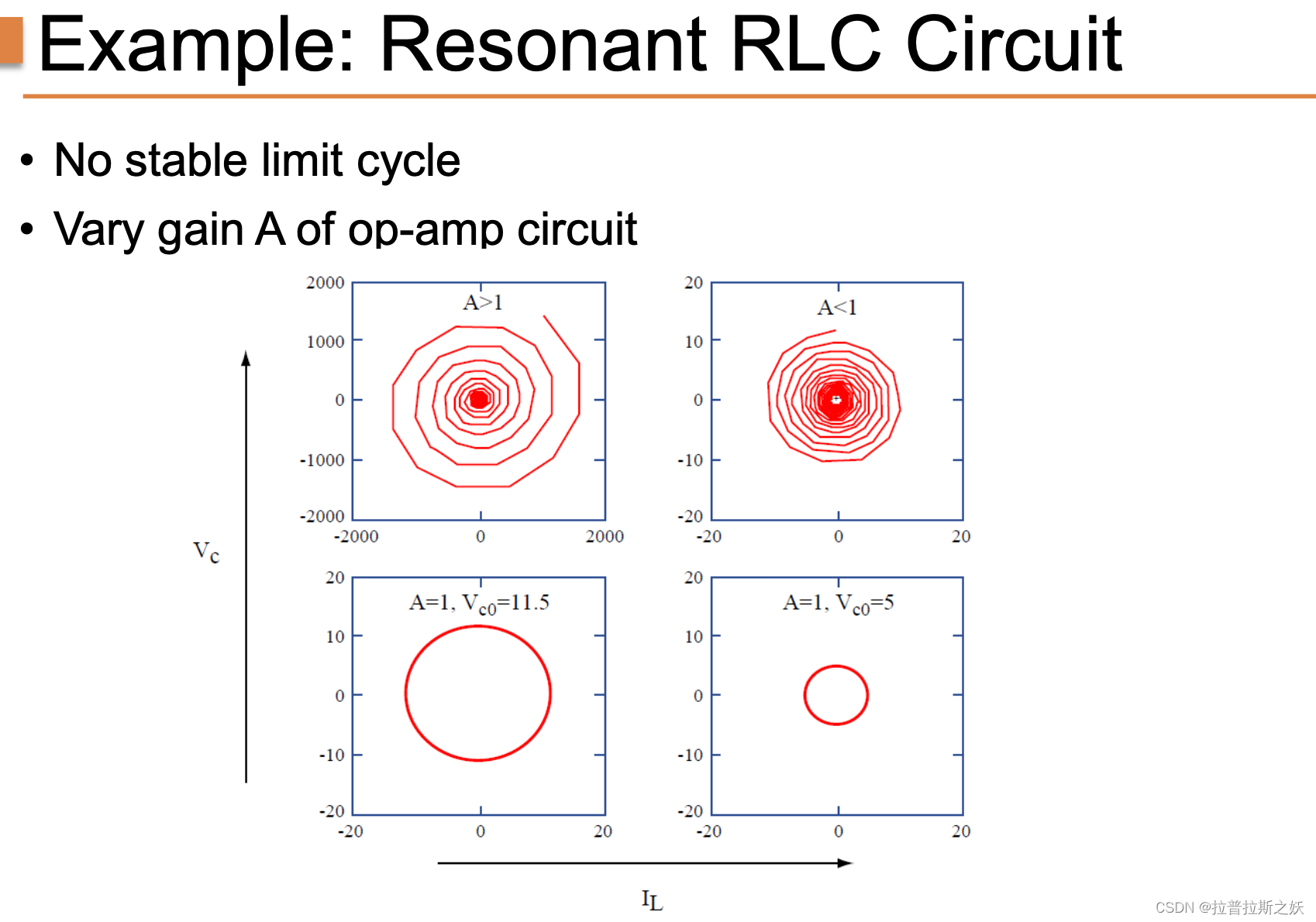
概述

RLC 电路是一个经典的二阶电路，由电阻 $R$、电感 $L$ 和电容 $C$ 组成。这个电路可以表现出不同的动态行为，具体取决于阻尼系数和激励条件。典型的 RLC 电路方程如下：

1. 电容电压 $v_C$ 的变化率：
   $$\frac{d{v}_C}{dt}=\frac{1}{C}{i}_L$$

2. 电感电流 $i_L$ 的变化率：
   $$\frac{d{i}_L}{dt}=\frac{1}{L}(v_S-v_C-i_{L}R)$$

理想放大器的限制

理论上，线性放大器可以产生一个无阻尼的线性系统，但它不能创建一个真正的振荡器。右图中展示了一个经典的负反馈放大器电路，其中包括了 RLC 电路。然而，由于放大器的固有特性，这样的电路无法实现持续的振荡。

电路分析

通过分析 RLC 电路的微分方程，可以得到以下关系：

1. 电容电压的微分方程：
   $$\frac{d{v}_C}{dt}=\frac{1}{C}{i}_L$$

2. 电感电流的微分方程：
   $$\frac{d{i}_L}{dt}=\frac{1}{L}(v_0-v_C-v_0)=-\frac{v_C}{L}$$

这些方程描述了电路的动态行为。

振荡器

通过增加限幅器实现振荡器

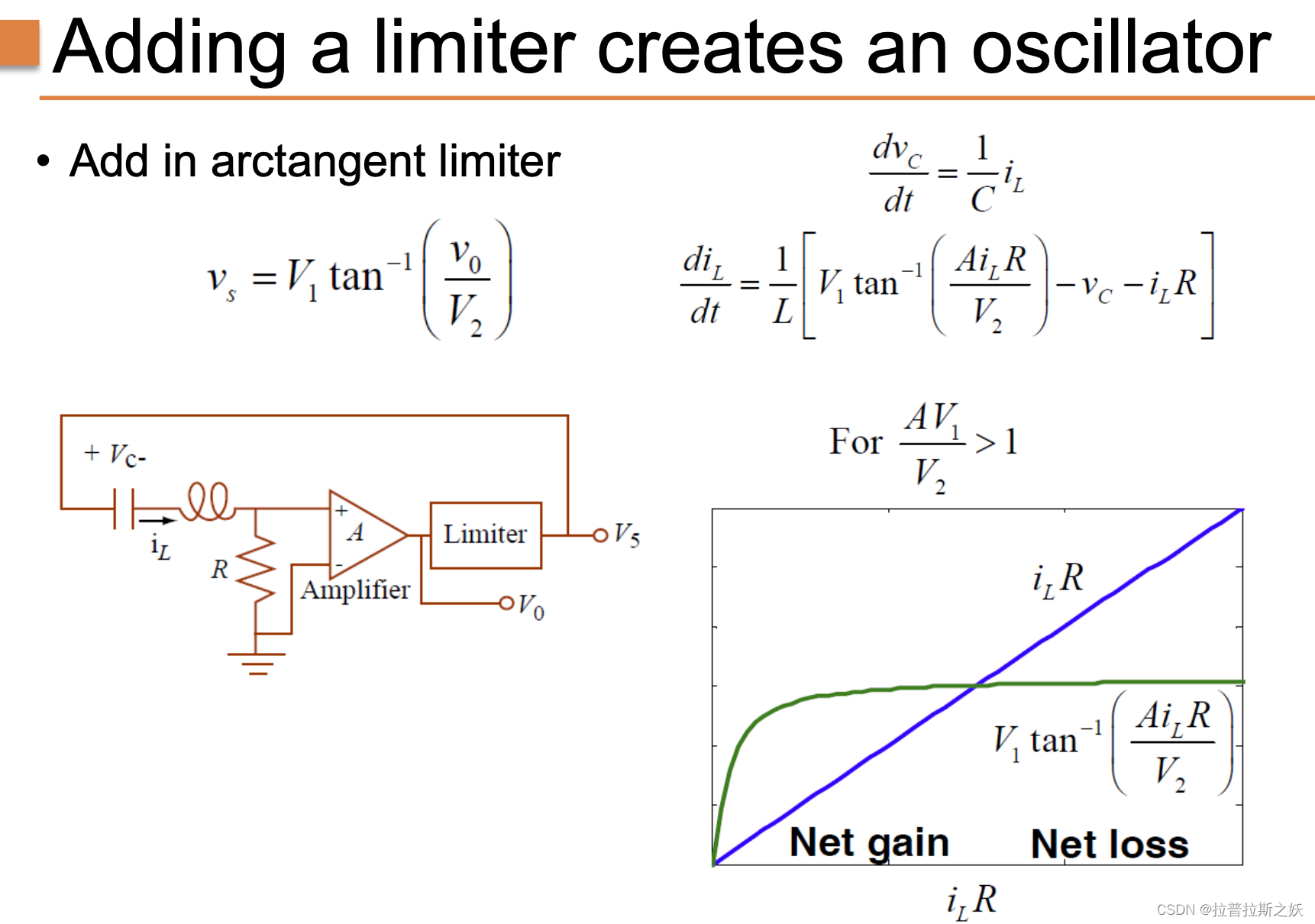
图表分析：

• 反正切限幅器: 在公式 $v_s=V_1{\tan }^{-1}\left(\frac{v_0}{V_2}\right)$ 中，引入了反正切限幅器。这一函数限制了输出电压，确保其不会无限制地增长，这是稳定电路振荡幅度的关键。
• 电路图: 示意图显示了一个带有放大器和限幅器的反馈环路，串联了一个包含电感 $L$、电容 $C$ 和电阻 $R$ 的电路。电感、电容和电阻的存在表明这是一个谐振电路，反馈用于控制振荡的幅度。
• 微分方程:
  • $\frac{d{v}_c}{dt}=\frac{1}{C}{i}_L$: 该方程描述了电容电压 $v_c$ 和电感电流 $i_L$ 之间的关系。
  • $\frac{d{i}_L}{dt}=\frac{1}{L}\left[V_1{\tan }^{-1}\left(\frac{A{i}_{L}R}{V_2}\right)-v_c-i_{L}R\right]$: 这是电感电流变化率的方程，包含了限幅器的影响。

数学含义：

反正切限幅器函数引入了一个非线性，这对控制振荡幅度至关重要。如果没有这种非线性，电路要么不会振荡，要么由于系统中的任何增益会导致振荡幅度不受控制地增长。反正切函数平滑了响应，确保输出保持在有界范围内。这是边际振荡器的特征，在边际振荡器中，振荡幅度稳定在某一水平，而不是持续增长。

边际振荡器的特性

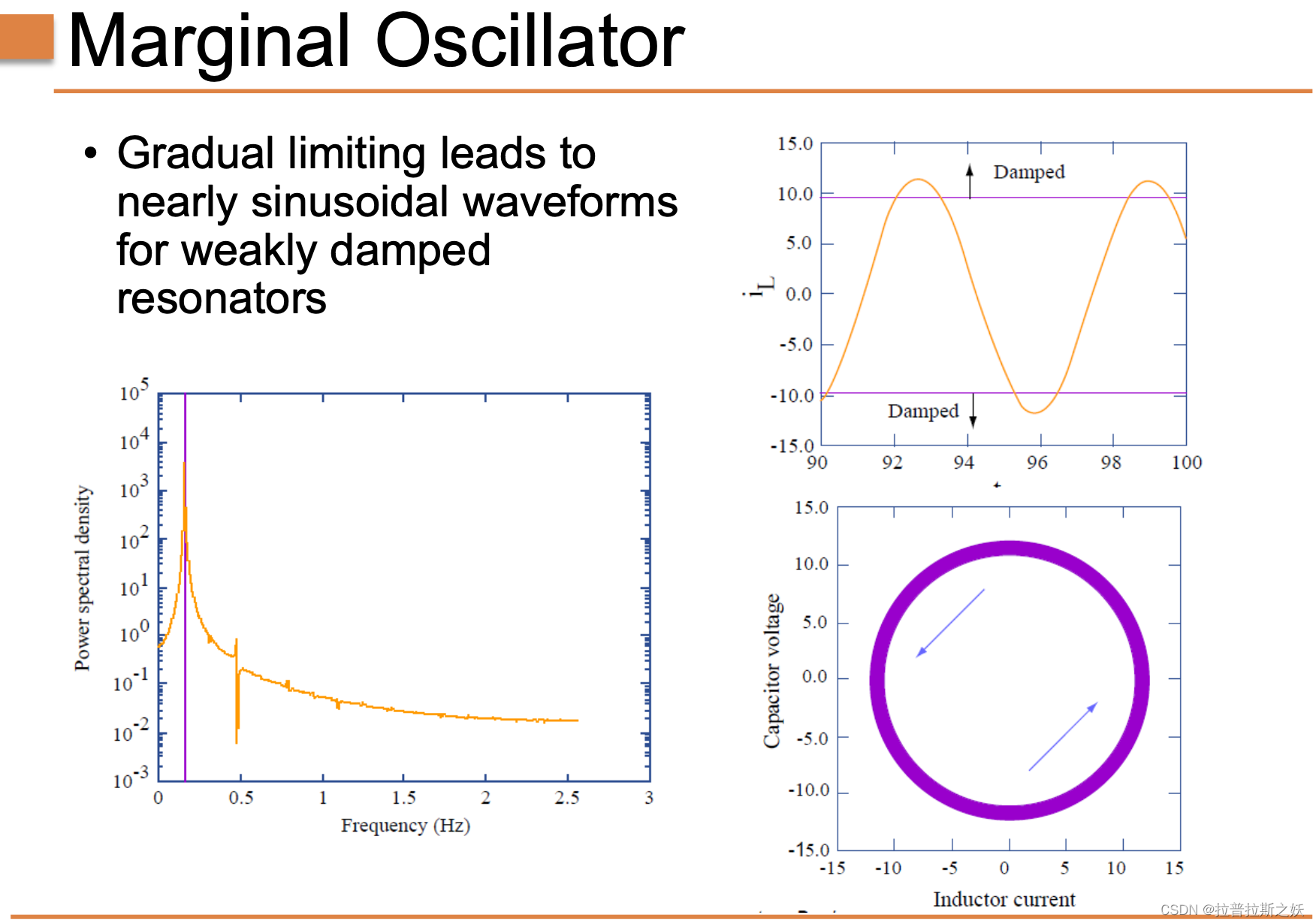
幻灯片分析：

• 正弦波形: 限幅函数导致接近正弦波形，尤其是在弱阻尼谐振器中。这在图表中得到了体现，显示了通过渐进的限幅，波形接近正弦形。
• 功率谱密度: 功率谱密度图显示振荡器主要输出在特定频率上，这表明其输出接近正弦。频谱在振荡频率处有一个峰值，而在其他频率上逐渐减小，反映了限幅机制在产生稳定振荡中的有效性。
• 相空间表示: 相空间图（右下方）显示了一个极限环，即一个稳定的闭合路径，表示振荡器的稳态行为。这显示了系统的动力学如何收敛到一个周期轨道，对于保持一致的振荡至关重要。

关键点：

• 弱阻尼: 渐进限幅在自然振荡未被显著衰减的弱阻尼系统中效果显著。
• 接近正弦输出: 输出保持接近正弦，这对于许多需要干净周期信号的应用是有利的。

振荡器的总结评论

关键见解：

• 谐振器与振荡器: 需要区分谐振器和振荡器。单独的谐振器不能维持振荡；它需要一个有源电路（振荡器）来补偿损耗。
• 非线性特性: 振荡器本质上是非线性的。这种非线性不是缺陷，而是定义稳定振荡幅度所必需的。
• 极限环动力学: 振荡器的极限环行为决定了其长期动力学。分析极限环周围的扰动可以提供关于系统在扰动后如何恢复到稳定振荡的见解。

本Lecture总结

• 反馈的好处:

  • 降低灵敏度: 反馈降低了对参数变化和外部干扰的灵敏度。
  • 减少响应时间: 提高系统响应速度，这对于需要快速驱动的应用至关重要。
  • 零直流误差: 通过消除直流误差，确保精确的稳态性能。
  • 稳定系统: 提供一种稳定本来不稳定系统的机制。

• 复杂性考虑: 虽然反馈提供了显著的优势，但其设计和实现可能很复杂，尤其是在需要精确稳定性的MEMS和其他高精度应用中。

• 系统分析: 包括频域、时域、根轨迹和状态空间分析在内的各种方法对于全面理解反馈系统及其在不同条件下的行为至关重要。

题目

以下是基于你提供的控制系统概念和内容，可能会在考试中出现的一些题目和答案：

1. Open-Loop Control

Question:
Explain the working principle of an open-loop control system using the example of a hot plate. What are the main limitations of this approach?
Answer:
An open-loop control system operates based on predefined settings without feedback. In the case of a hot plate, the system is calibrated to achieve a desired temperature using a controller with a first-order response and no dynamics. The main limitations include sensitivity to disturbances and drifts, causing steady-state errors because there is no feedback to correct deviations.

中文问题：
解释开环控制系统的工作原理，并以热板为例说明。这种方法的主要局限性是什么？
中文答案：
开环控制系统基于预设值操作，没有反馈。对于热板系统，通过标定来达到预期温度，控制器具有一阶响应且无动态特性。主要局限性包括对扰动和漂移的敏感性，导致稳态误差，因为没有反馈来纠正偏差。

2. Feedback Control and Proportional Control

Question:
Describe how proportional control is used to limit sensitivity to variations in a system. Include the closed-loop transfer function in your explanation.
Answer:
Proportional control adds a term proportional to the error to limit system sensitivity to variations. The closed-loop transfer function is given by ( \frac{HK}{1+HK} ). This reduces steady-state error as ( K_0 ) increases, although the system response time and bandwidth are also affected.

中文问题：
描述如何使用比例控制来限制系统对变化的敏感性。请在解释中包含闭环传递函数。
中文答案：
比例控制通过增加一个与误差成比例的项来限制系统对变化的敏感性。闭环传递函数为( \frac{HK}{1+HK} )。随着( K_0 )的增加，这可以减少稳态误差，但系统响应时间和带宽也会受到影响。

3. Second-Order System Control

Question:
Explain the control strategy for a second-order system using a vibration sensor. How does the Q factor influence the system response?
Answer:
For a second-order system such as a vibration sensor, the control strategy involves using feedback to maintain a constant gap by measuring vibration. The Q factor, representing the damping ratio, influences the system response: a higher Q indicates less damping and more oscillatory behavior, while a lower Q indicates more damping and a faster settling time.

中文问题：
解释使用振动传感器控制二阶系统的策略。Q因子如何影响系统响应？
中文答案：
对于二阶系统，如振动传感器，控制策略包括通过测量振动来保持恒定间隙。Q因子表示阻尼比，影响系统响应：较高的Q表示阻尼较小且振荡行为更多，而较低的Q表示阻尼较大且稳定时间更快。

4. Nonlinear System Feedback

Question:
How does feedback control in a nonlinear system differ from a linear system? Provide an example using the provided control block diagram.
Answer:
In a nonlinear system, feedback control involves predistorting the control signal to compensate for plant nonlinearities. The control block diagram shows that the controller adjusts the error signal to achieve a linearized output. An example is the use of a tangent function to correct the control signal, maintaining system stability across a wide input range.

中文问题：
非线性系统中的反馈控制与线性系统有何不同？请使用提供的控制框图举例说明。
中文答案：
在非线性系统中，反馈控制包括预先扭曲控制信号以补偿系统的非线性。控制框图显示，控制器调整误差信号以实现线性输出。一个例子是使用反正切函数校正控制信号，保持系统在广泛输入范围内的稳定性。

5. PID Control

Question:
Describe the benefits and drawbacks of using PID control in a system. How does adding a differential term improve system performance?
Answer:
PID control combines proportional, integral, and differential terms to improve system performance. The benefits include better DC tracking with the integral term and anticipation of future errors with the differential term. However, the drawbacks include the potential for increased ringing and instability due to the additional poles introduced by the integral and differential terms.

中文问题：
描述在系统中使用PID控制的优缺点。增加微分项如何改善系统性能？
中文答案：
PID控制结合了比例、积分和微分项以改善系统性能。优点包括通过积分项实现更好的直流跟踪，通过微分项预测未来误差。然而，缺点包括由于积分和微分项引入的额外极点，可能增加振荡和不稳定性。

6. Oscillators and Limit Cycles

Question:
What is the difference between a resonator and an oscillator? Explain how a limit cycle is formed in an oscillator.
Answer:
A resonator is a passive element that exhibits underdamped oscillatory behavior, whereas an oscillator includes a resonator and an active gain element that compensates for losses, resulting in steady oscillations. A limit cycle is formed in an oscillator when nonlinearities in the system create a stable closed path in state space, ensuring continuous oscillation at a fixed amplitude.

中文问题：
谐振器和振荡器有什么区别？解释极限环在振荡器中是如何形成的。
中文答案：
谐振器是一个表现出欠阻尼振荡行为的被动元件，而振荡器包括谐振器和补偿损耗的主动增益元件，产生稳定的振荡。极限环在振荡器中形成，是由于系统中的非线性产生了状态空间中的稳定闭合路径，确保在固定幅度下连续振荡。

这些题目和答案涵盖了控制系统的关键概念和应用，希望对你的考试准备有所帮助。

继续基于你提供的控制系统内容设计一些可能的考试题目及其答案。

7. Stability Analysis

Question:
Explain how the Routh-Hurwitz criterion can be used to determine the stability of a third-order system. Provide an example using a system with three poles.
Answer:
The Routh-Hurwitz criterion provides a systematic method to determine the stability of a system by constructing a Routh array and examining the sign changes in the first column. For a third-order system, the characteristic equation can be expressed as (a_3s^3 + a_2s^2 + a_1s + a_0 = 0). The system is stable if all coefficients in the Routh array are positive. An example system with the characteristic equation (s^3 + 2s^2 + 3s + 4 = 0) would have a Routh array showing no sign changes in the first column, indicating stability.

中文问题：
解释如何使用劳斯-赫尔维茨判据来确定三阶系统的稳定性。举一个包含三个极点的系统的例子。
中文答案：
劳斯-赫尔维茨判据通过构建劳斯阵列并检查第一列中的符号变化，提供了一种系统方法来确定系统的稳定性。对于三阶系统，特征方程可以表示为 (a_3s^3 + a_2s^2 + a_1s + a_0 = 0)。如果劳斯阵列中的所有系数均为正，则系统稳定。一个特征方程为 (s^3 + 2s^2 + 3s + 4 = 0) 的系统例子，其劳斯阵列在第一列中没有符号变化，表明系统稳定。

8. Effect of Controller Bandwidth

Question:
Discuss the impact of controller bandwidth on the overall system response. How does the controller bandwidth being less than the plant bandwidth affect the system?
Answer:
Controller bandwidth significantly influences the overall system response. If the controller bandwidth is less than the plant bandwidth, the controller will dominate the system response, potentially leading to slower response times and reduced system performance. This is because the controller cannot respond quickly enough to changes in the plant, resulting in a lagged and less precise control action.

中文问题：
讨论控制器带宽对整体系统响应的影响。控制器带宽小于植物带宽会如何影响系统？
中文答案：
控制器带宽对整体系统响应有显著影响。如果控制器带宽小于植物带宽，控制器将主导系统响应，可能导致响应时间变慢和系统性能降低。这是因为控制器无法足够快地响应植物的变化，导致控制动作滞后且不精确。

9. PI Control in Nonlinear Systems

Question:
Explain how PI (Proportional-Integral) control can eliminate steady-state errors in nonlinear systems. Use the given example of an arctangent limiter to illustrate your point.
Answer:
PI control adds an integral term to the proportional control, which accumulates the error over time and drives it to zero, thus eliminating steady-state errors. In a nonlinear system with an arctangent limiter, the integral action ensures that the output closely follows the input by continuously adjusting for any persistent discrepancies. The arctangent function helps in managing the nonlinearity by smoothly limiting the control signal.

中文问题：
解释PI（比例-积分）控制如何消除非线性系统中的稳态误差。使用反正切限幅器的例子来说明你的观点。
中文答案：
PI控制在比例控制的基础上增加了积分项，积分项会随着时间累积误差并将其驱零，从而消除稳态误差。在带有反正切限幅器的非线性系统中，积分作用确保输出紧随输入，通过持续调整任何持续存在的差异。反正切函数通过平滑限制控制信号来管理非线性。

10. Oscillator Design

Question:
Describe the role of a limiter in oscillator design. How does adding an arctangent limiter help in achieving stable oscillations?
Answer:
A limiter in oscillator design restricts the amplitude of the oscillations to prevent them from growing indefinitely, which could lead to instability. Adding an arctangent limiter introduces a nonlinear element that smooths out the oscillation amplitude, ensuring that the system remains within desired limits. This helps in achieving stable oscillations by balancing the gain and loss within the system.

中文问题：
描述限幅器在振荡器设计中的作用。添加反正切限幅器如何帮助实现稳定的振荡？
中文答案：
限幅器在振荡器设计中限制振荡幅度，防止其无限增长导致不稳定。添加反正切限幅器引入了一个非线性元件，平滑振荡幅度，确保系统保持在预定范围内。通过平衡系统内的增益和损耗，这有助于实现稳定的振荡。

11. MEMS Control

Question:
Explain the potential advantages of running a MEMS-based system in closed-loop mode as opposed to open-loop mode. What challenges might arise in implementing closed-loop control in MEMS?
Answer:
Running a MEMS-based system in closed-loop mode can significantly improve accuracy and stability by continuously adjusting for disturbances and drifts. The advantages include better precision in positioning and force control, and enhanced system robustness. However, challenges in implementing closed-loop control in MEMS include the need for precise and reliable sensors, fast and efficient actuators, and sophisticated control algorithms to handle the microscale dynamics and potential nonlinearities.

中文问题：
解释相对于开环模式，运行闭环模式的MEMS系统的潜在优势。在MEMS中实现闭环控制可能会遇到哪些挑战？
中文答案：
运行闭环模式的MEMS系统通过持续调整扰动和漂移，可以显著提高精度和稳定性。优势包括更高的定位和力控精度，以及增强的系统鲁棒性。然而，在MEMS中实现闭环控制的挑战包括需要精确可靠的传感器、快速高效的执行器以及复杂的控制算法来处理微尺度动态和潜在的非线性。

12. Limit Cycles in Nonlinear Systems

Question:
What is a limit cycle in the context of nonlinear systems? How can limit cycles be identified and analyzed?
Answer:
A limit cycle is a stable, closed trajectory in the state space of a nonlinear system where the system’s behavior repeats periodically. Limit cycles can be identified using phase plane analysis, where the state variables are plotted against each other to reveal closed loops. Analysis involves determining the stability and period of the limit cycle, which can be done using methods such as the Poincaré-Bendixson theorem and numerical simulations.

中文问题：
在非线性系统中，什么是极限环？如何识别和分析极限环？
中文答案：
极限环是非线性系统状态空间中的稳定闭合轨迹，系统行为在其中周期性重复。极限环可以通过相平面分析识别，在相平面中将状态变量相互对比绘图，揭示闭合环。分析包括确定极限环的稳定性和周期，这可以通过庞加莱-本迪克森定理和数值模拟等方法实现。

这些题目和答案涵盖了控制系统理论的重要方面，希望对你的学习和考试准备有帮助。如果需要更多特定领域的问题或进一步详细的解答，请随时告知。

这篇关于MEMS：Lecture 18 Feedback的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---