凸规划理论——计算几何，凸集，超平面，凸函数，凸规划判别

本文主要是介绍凸规划理论——计算几何，凸集，超平面，凸函数，凸规划判别，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、计算几何是研究什么的？

计算几何研究的对象是几何图形。
计算几何作为CAD的基础理论之一，主要研究内容是几何形体的数学描述和计算机表述。

二、计算几何理论中（或凸集中）过两点的一条直线的表达式，是如何描述的？与初中数学中那些直线方程有什么差异？

对一元函数f(x)在几何上af(x1)+(1-a)f(x2)=0 (0≤a≤1)表示连接（x1,f(x1)),(x2,f(x2))的线段
f(ax1+(1-a)x2)表示在点 ax1+(1-a)x2处的函数值。
也就是说，一元凸函数表示连接函数图形上任意两点的线段总是位于曲线弧的上方。

初中数学中直线方程的表示：

一般式:Ax+By+C=0
点斜式:y-y0=k(x-x0)（斜率为k，且过点（x0,y0））
截距式:x/a+y/b=1（表示与x轴、y轴相交，且x轴截距为a，y轴截距为b的直线）
斜截式:y=kx+b（表示斜率为k且y轴截距为b的直线）
两点式：
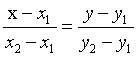(x1≠x2，y1≠y2)

交点式: f1(x,y) *m+f2(x,y)=0（表示过直线f1(x,y)=0与直线f2(x,y)=0的交点的直线）
点平式:f(x,y) -f(x0,y0)=0（表示过点（x0,y0）且与直线f（x,y）=0平行的直线）
法线式：xcosα+ysinα-p=0（过原点向直线做一条的垂线段，该垂线段所在直线的倾斜角为α，p是该线段的长度）
点向式：(x-x0)/u=(y-y0)/v (u≠0,v≠0)（表示过点(x0,y0)且方向向量为（u,v ）的直线）
法向式：a（x-x0）+b（y-y0）=0 （表示过点（x0，y0）且与向量（a，b）垂直的直线）

三、凸集是什么？ 直线是凸集吗？是仿射集吗？

凸集是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。

在一维空间中，凸集是单点或一条不间断的线（包括直线、射线、线段）；二、三维空间中的凸集就是直观上凸的图形。（在二维中有扇面、圆、椭圆等，在三维中有实心球体等；多数情况下，两个凸集的交集也是凸集，空集也是凸集）

如果一个集合c是仿射集，那么

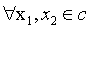
ax1+(1-a)x2这个点（过x1, x2的直线上的点）也在集合c内。(一条直线上的点组成的集合是仿射集，一个二维平面上的点组成的集合也是仿射集；但是线段就不是仿射集了)。

四、三维空间中的一个平面，如何表达？

一般方程：
Ax+By+Cz+D=0
点法式方程：
A(x-x0)+B(y-y0)+C(z-z0)=0
点向式方程：
(x-x0)/A=(y-y0)/B=(z-z0)/C
截距式方程：
x/a+y/b+z/c=1
法线式方程：
xcosα+ycosβ+zcosγ=p

五、更高维度的“超平面”，如何表达？

n 维空间中的超平面由下面的方程确定:

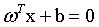
其中，w 和 x 都是 n 维列向量，x 为平面上的点，w 为平面上的法向量，决定了超平面的方向，b 是一个实数，代表超平面到原点的距离。且

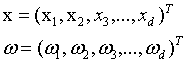
六、什么是“凸函数”定义？什么是Hessen矩阵? 如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？

1.凸函数的定义

对于一元函数f(x)如果对于任意tϵ[0,1]均满足：f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2) 则称f(x)为凸函数

如果对于任意tϵ(0,1)均满足：f(tx1+(1−t)x2)<tf(x1)+(1−t)f(x2)，则称f(x)为严格凸函数

2.Hessen矩阵

由高等数学知识可知，若一元函数f(x)在x=x(0)点的某个领域内具有任意阶导数，则f(x)在x(0)点处的泰勒展开式为：

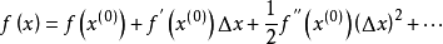
其中

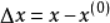
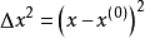
二元函数

f(x1,x2)在

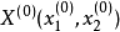
点处的泰勒展开式为：

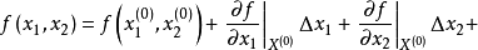
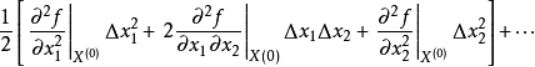
其中

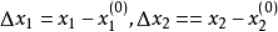
将上述展开式写成矩阵形式，则有：

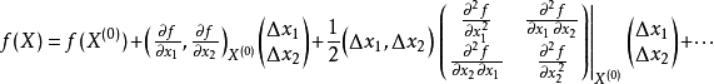
即

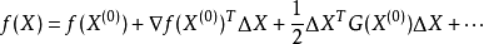
其中：

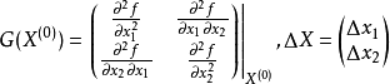
G(x(0))是f(x1,x2)在x(0)点处的Hessen矩阵。它是由函数f(x1,x2)在x(0)点处的二阶偏导数所组成的方阵。

多元函数

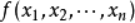
在x(0)点处的泰勒展开式的矩阵形式为：

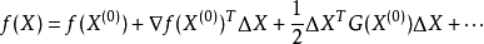
其中：

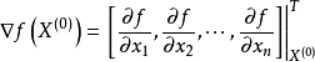
是f(x)在点x(0)处的梯度

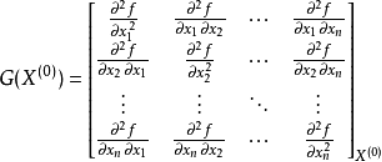
为函数f(x)在x(0)点处的Hessen矩阵。

Hessen矩阵是由目标函数 在点X处的二阶偏导数组成的 阶对称矩阵

3.判别一个函数是凸函数

对于一元函数f(x)，我们可以通过其二阶导数f″(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0f″(x)≥0 ，则f(x)是凸函数

对于多元函数f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)凸函数

4. f(x)=x^3 函数是凸函数吗？

由3，我们可以很容易知道f’(x)=3x²，f’’(x)=6x，而对于一元函数的凸函数来说若f’’(x)总是非负则f(x)为凸函数，而f(x)=x^3 的二阶导数为f’’(x)=6x不总是非负，所以f(x)=x^3 不是凸函数。

七、什么是“凸规划”？如何判别一个规划问题是凸规划问题。举例说明？

1.凸规划

若最优化问题的目标函数为凸函数，不等式约束函数也为凸函数，等式约束函数是仿射的，则称该最优化问题为凸规划。凸规划的可行域为凸集，因而凸规划的局部最优解就是它的全局最优解。当凸规划的目标函数为严格凸函数时，若存在最优解，则这个最优解一定是唯一的最优解。

2.判别凸规划问题

参考文章

https://blog.csdn.net/denghecsdn/article/details/77313758
https://www.cnblogs.com/always-fight/p/9377554.html

这篇关于凸规划理论——计算几何，凸集，超平面，凸函数，凸规划判别的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---