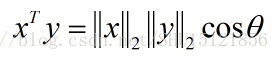超平面专题
机器学习系列(15)_SVM碎碎念part3:如何找到最优分离超平面
作者:寒小阳 时间:2016年9月。 出处:http://blog.csdn.net/han_xiaoyang/article/details/52683653 声明:版权所有,转载请联系作者并注明出处 1.引言 是的,咱们第1篇blog介绍了目标;第2篇blog介绍了向量相关的背景数学知识,看到了如何求解Margin的值;今天这个部分主要目的是和大家一起来看看,选择
凸规划理论——计算几何,凸集,超平面,凸函数,凸规划判别
文章目录 一、计算几何是研究什么的?二、计算几何理论中(或凸集中)过两点的一条直线的表达式,是如何描述的?与初中数学中那些直线方程有什么差异?三、凸集是什么? 直线是凸集吗?是仿射集吗?四、三维空间中的一个平面,如何表达?五、更高维度的“超平面”,如何表达?六、什么是“凸函数”定义?什么是Hessen矩阵? 如何判别一个函数是凸函数?f(x)=x^3 函数是凸函数吗?1.凸函数的定义2.He
样本点到SVM超平面的距离
计算超平面系数 estimator_svm = svm.SVC(kernel="linear", C=1, gamma=1)#创建SVM模型estimator_svm.fit(x_train, y_train)#训练模型svm_predict = estimator_svm.predict
【ML学习笔记】5:机器学习中的数学基础5(张量,哈达玛积,生成子空间,超平面,范数)
向量/矩阵/张量 向量 向量可以表示成一维数组,每个分量可以理解为向量所表示的点在空间中坐标的分量。 矩阵 矩阵可以表示成二维数组,上节理解了矩阵可以理解为线性映射在特定基下的一种定量描述。 张量 张量可以表示成任意维的数组,张量是向量概念向更高阶次的推广,向量是一维张量。 但不能把矩阵简单的看成二维张量,张量是几何的,矩阵是代数的。二阶张量和矩阵概念不同,但可以建立联系,矩阵可以描
SVM 支持向量机,如何寻找超平面的
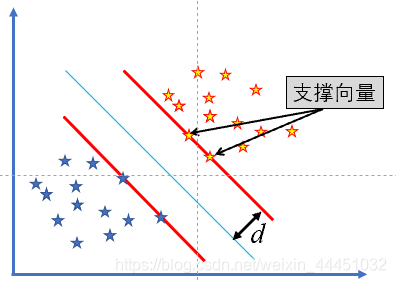
SVM 支持向量机,如何寻找超平面的? 1.SVM概念 支持向量机(Support Vector Machine, SVM)是一种二分类模型,目标是寻找一个标准(称为超平面)对样本数据进行分割,分割的原则是确保分类最优化(类别之间的间隔最大)。 1.1 分类 下图绿色和黄色,红色可以基本建红色和黄色划分开 用到CV2的向量机模块 2.1 cv2.ml.SVM_cre
支持向量机SVM——最大间隔分离超平面的计算、拉格朗日乘数法求解不等式约束的优化问题
支持向量机SVM——最大间隔分离超平面的计算 如何定义两个集合的最优分隔超平面呢? 找到集合"边界"上的若干点,以这些点为基础计算超平面的方向,以二维坐标平面为例子 w T x + b = 0 w^Tx+b=0 wTx+b=0,当系数 w T w^T wT确定的时候,这个超平面的方向也就随之确定,以两个结果边界上的点的平均作为超平面的"截距"。 SVM线性分类问题 假设给定一个特征空
复盘:手推SVM支持向量机二分类超平面,求解目标函数原问题,kkt条件,对偶问题求q,核函数、hinge loss损失函数,硬间隔,软间隔,最后得到w和b
复盘:手推SVM支持向量机二分类超平面,求解目标函数原问题,kkt条件,对偶问题求q,核函数、hinge loss损失函数,硬间隔,软间隔,最后得到w和b 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备的 (1)自己的科研经历,科研内容,学习的相关领域知识,要熟悉熟透了 (2)自己的实习经历
任意一点X0到超平面S的距离以及拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
转自: http://blog.csdn.net/xinzaichenmo/article/details/70161728 http://blog.csdn.net/xianlingmao/article/details/7919597 在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条
谁都能学会的SVM(支持向量机)分类器(一)超平面篇
谁都能学会的SVM(支持向量机)分类器(一)超平面篇 机器学习领域问题实现模式一般为特征+分类器,SVM分类器在机器学习分类器领域地位举足轻重。 SVM擅长解决什么类型的问题呢? 1.小样本 2.非线性(松弛变量、核函数为SVM精髓) 3.高维模式识别(例如文本分类) 从感知机开始,引入超平面的概念 n 维空间中的超平面由下面的方程确定: w T x + b = 0 w^Tx+b=0 wT
深度神经网络的数学原理:基于超平面、半空间与线性区域的表示
概述 以前的文章主要描述了神经网络,即多层感知机、全连接模型的运行原理,还是以实验为主,数学描述为辅的方式,这篇文章以纯数学的视角来描述神经网络的运行原理,主要以前馈过程为主(反向传播的动力学过程还是比较复杂,正向过程还未完全研究清楚,暂时还未考虑)。 半空间 在讲半空间(Halfspace)时,需要引入分离超平面(Separating Hyperplane)的概念,这里简单介绍分离超平面的
超平面的理解与公式推导
研究了半天,终于对“超平面”有了个初步了解。 n 维空间中的超平面由下面的方程确定: 其中,w 和 x 都是 n 维列向量,x 为平面上的点,w 为平面上的法向量,决定了超平面的方向,b 是一个实数,代表超平面到原点的距离。且
凸优化学习笔记 2:超平面分离定理
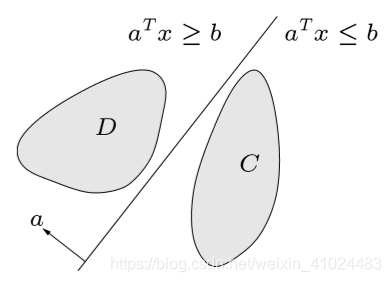
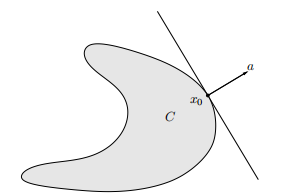
个人博客地址 Glooow,欢迎光临~~~ 文章目录 1. 超平面分离定理2. 支撑超平面定理 1. 超平面分离定理 超平面分离定理(Separating hyperplane theorem):若 C , D C,D C,D 为非空凸集,且 C ∩ D = ∅ C\cap D=\varnothing C∩D=∅,则存在 a ≠ 0 , b a\ne 0,b a
凸集之分离与支撑超平面
分离与支撑超平面(Separating and supporting hyperplanes) 1.分离超平面定理 定理:假设C和D是两个不相交的凸集,即C∩D=∅。然后存在一个a≠0和b,这样aTx≤b用于所有x∈C,aTx≥b用于所有x∈D。 换句话说,仿射函数aTx−b,在C上非正,在D上非负. 超平面{x|aTx=b}称为分离C和D的分离超平面,或者称为分离C和D。 如图所示,超平面{