文章目录 一、计算几何是研究什么的？二、计算几何理论中（或凸集中）过两点的一条直线的表达式，是如何描述的？与初中数学中那些直线方程有什么差异？三、凸集是什么？ 直线是凸集吗？是仿射集吗？四、三维空间中的一个平面，如何表达？五、更高维度的“超平面”，如何表达？六、什么是“凸函数”定义？什么是Hessen矩阵? 如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？1.凸函数的定义2.He

文章目录 1 凸集2 凸函数2.1 凸函数性质2.2 一阶判别公式2.3 二阶判别公式 3 凸规划 1 凸集 设集合 S ⊂ R n S\subset \R^n S⊂Rn，若 S S S中任意两点连线仍属于 S S S，则 S S S称为凸集，即 x 1 + λ ( x 2 − x 1 ) ∈ S \bm x_1 + \lambda(\bm x_2 - \bm x_1) \

凸集也叫凸子集。 对于一个集合S，如果集合中任何两点的连线上的所有点都在该集合内，就称集合S是凸集。 对于凸集，设X和Y是集合中的任何两点，  并且，那么也在该集合内。 例如，对于欧式空间，实心的球体就是凸集，但中空的球就不是凸集。

Welcome To My Blog Rockafeller说:”优化问题的分水岭不是线性和非线性,而是凸性和非凸性” 两点连线上的点 在介绍凸集和凸函数之前,先来看一个与之有关的基本问题: 如下图,已知空间中有B,C两点,在给定两点坐标的情况下如何量化B,C连线上的任意一点D? 很简单,看下图,设已知A,B,C,D的坐标, AD = AB + BD = AB + kBC (D在

目录 一、计算几何1.什么是计算几何2.计算几何理论中过两点的一条直线的表达式，是如何描述的？ 二、凸集1.什么是凸集2.如何表达三维空间中的一个平面3.如何表达超平面4.什么是凸函数及如何判别5.什么是凸规划及如何判别 一、计算几何 1.什么是计算几何 计算几何是计算机理论科学的一个重要分支.自20世纪70年代末从算法设计与分析中独立出来起，不到30年，该学科已经有了巨大的

为什么研究凸优化先要从凸集的性质开始： 凸函数图像的上方区域，一定是凸集；  假如一个函数上方是凸集，这个函数就是凸函数 如何用向量表示几何体    什么是凸包         包含凸集的最小集合         如何计算一个凸集的 凸包是什么？时间复杂度是多少                 转化为排序问题，时间复杂度是nlogn  凸集基本概念

1、几种简单的凸集 仿射集凸集 R n R^n Rn空间、 R n R^n Rn空间子空间、直线任意线段、${x_0+\theta v 2、超平面与半空间 超平面（Hyperplane）: { x ∣ a T x = b } \{x|a^T x=b\} {x∣aTx=b} x , a ∈ R n , b ∈ R , a ≠ 0 x,a \in R^n,b \in R, a \neq 0 x

凸集与凸集分离定理、Farkas引理 文章目录 凸集与凸集分离定理、Farkas引理凸集定义：凸集凸集性质（逐个证明） 超平面定义：超平面证明：超平面是凸集定义：支撑超平面定义：多面体定义：凸锥 凸集分离定理定义：分离定义：凸集分离定理 Farkas引理定义：Farkas引理证明：Farkas引理 凸集 定义：凸集 注意凸集的定义，任取两点满足某个条件为凸集： 证明

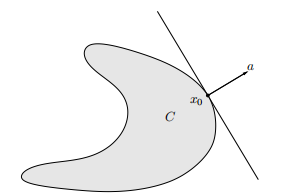
分离与支撑超平面（Separating and supporting hyperplanes） 1.分离超平面定理 定理：假设C和D是两个不相交的凸集，即C∩D=∅。然后存在一个a≠0和b，这样aTx≤b用于所有x∈C，aTx≥b用于所有x∈D。 换句话说，仿射函数aTx−b,在C上非正，在D上非负. 超平面{x|aTx=b}称为分离C和D的分离超平面，或者称为分离C和D。 如图所示，超平面{