本文主要是介绍凸集、凸函数与凸规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1 凸集
- 2 凸函数
- 2.1 凸函数性质
- 2.2 一阶判别公式
- 2.3 二阶判别公式
- 3 凸规划
1 凸集
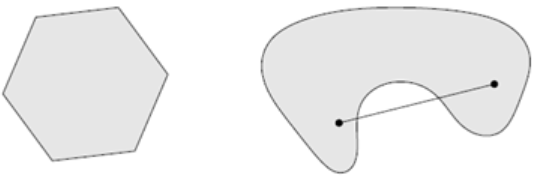
设集合 S ⊂ R n S\subset \R^n S⊂Rn,若 S S S中任意两点连线仍属于 S S S,则 S S S称为凸集,即
x 1 + λ ( x 2 − x 1 ) ∈ S \bm x_1 + \lambda(\bm x_2 - \bm x_1) \in S x1+λ(x2−x1)∈S
2 凸函数
设 S S S为 R n \R^n Rn上的非空凸集, f f f是定义在 S S S上的实函数,若对任意 x 1 , x 2 ∈ S \bm x_1, \bm x_2 \in S x1,x2∈S,及 λ ∈ ( 0 , 1 ) \lambda \in (0, 1) λ∈(0,1),都有
f ( x 1 + λ ( x 2 − x 1 ) ) ≤ f ( x 1 ) + λ [ f ( x 2 ) − f ( x 1 ) ] f(\bm x_1+\lambda(\bm x_2 - \bm x_1))\leq f(\bm x_1) + \lambda[f(\bm x_2) - f(\bm x_1)] f(x1+λ(x2−x1))≤f(x1)+λ[f(x2)−f(x1)]
则称 f f f为 S S S上的凸函数。
对于一元函数 f f f,凸函数的几何解释可简单理解为曲线 f f f上任意两点的弦不在曲线下方,如下图所示。

一元凸函数的几何证明
若 ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) (x_1, f(x_1)), (x_2, f(x_2)) (x1,f(x1)),(x2,f(x2))为曲线 f f f上的两点,且满足 x 1 < x < x 2 x_1< x < x_2 x1<x<x2,由直线的两点式公式
y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1 \frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1} y2−y1y−y1=x2−x1x−x1
知,该两点构成的弦所在直线的方程为
y − f ( x 1 ) f ( x 2 ) − f ( x 1 ) = x − x 1 x 2 − x 1 \frac{y-f(x_1)}{f(x_2)-f(x_1)}=\frac{x-x_1}{x_2-x_1} f(x2)−f(x1)y−f(x1)=x2−x1x−x1由于弦上的点不小于对应曲线上的点,令 0 < λ < 1 0\lt\lambda\lt1 0<λ<1, x = x 1 + λ ( x 2 − x 1 ) x=x_1+\lambda(x_2-x_1) x=x1+λ(x2−x1),得
y ≥ f ( x )    ⟹    f ( x 1 + λ ( x 2 − x 1 ) ) − f ( x 1 ) f ( x 2 ) − f ( x 1 ) ≤ x 1 + λ ( x 2 − x 1 ) − x 1 x 2 − x 1 y\geq f(x) \implies \frac{f(x_1+\lambda(x_2-x_1))-f(x_1)}{f(x_2)-f(x_1)}\leq\frac{x_1+\lambda(x_2-x_1)-x_1}{x_2-x_1} y≥f(x)⟹f(x2)−f(x1)f(x1+λ(x2−x1))−f(x1)≤x2−x1x1+λ(x2−x1)−x1因此 f ( x 1 + λ ( x 2 − x 1 ) ) ≤ f ( x 1 ) + λ ( f ( x 2 ) − f ( x 1 ) ) f(x_1+\lambda(x_2-x_1)) \leq f(x_1)+\lambda(f(x_2)-f(x_1)) f(x1+λ(x2−x1))≤f(x1)+λ(f(x2)−f(x1)),不等式得证。
2.1 凸函数性质
凸函数的局部极小点是全局极小点。
证明: 若 x ∗ \bm x^* x∗是凸函数 f ( x ) f(\bm x) f(x)的局部极小点,假设 ∃ x ^ ∈ S \exists\hat \bm x \in S ∃x^∈S,使得 f ( x ∗ ) > f ( x ^ ) f(\bm x^*) > f(\hat \bm x) f(x∗)>f(x^),则对任意 λ ∈ ( 0 , 1 ) \lambda \in(0, 1) λ∈(0,1),由凸集性质有
x ∗ + λ ( x ^ − x ∗ ) ∈ S \bm x^* + \lambda(\hat \bm x - \bm x^*) \in S x∗+λ(x^−x∗)∈S因此
f ( x ∗ + λ ( x ^ − x ∗ ) ) ≤ f ( x ∗ ) + λ [ f ( x ^ ) − f ( x ∗ ) ] < f ( x ∗ ) f(\bm x^* + \lambda(\hat \bm x - \bm x^*))\leq f(\bm x^*) + \lambda[f(\hat\bm x) - f(\bm x^*)] <f(\bm x^*) f(x∗+λ(x^−x∗))≤f(x∗)+λ[f(x^)−f(x∗)]<f(x∗)
上述不等式表明,对任意 λ ∈ ( 0 , 1 ) \lambda \in (0, 1) λ∈(0,1)都存在 f ( x ∗ + λ ( x ^ − x ∗ ) ) < f ( x ∗ ) f(\bm x^* + \lambda(\hat \bm x - \bm x^*)) \lt f(\bm x^*) f(x∗+λ(x^−x∗))<f(x∗),显然与 f ( x ∗ ) f(\bm x^*) f(x∗)是极小值矛盾。
2.2 一阶判别公式
设 f f f是定义在凸集 S S S上的可微函数,则 f f f为凸函数的充要条件是,对任意 x 1 , x 2 ∈ S \bm x_1, \bm x_2 \in S x1,x2∈S,有
f ( x 2 ) ≥ f ( x 1 ) + ∇ f ( x 1 ) T ( x 2 − x 1 ) f(\bm x_2)\geq f(\bm x_1)+\nabla f(\bm x_1)^T(\bm x_2 - \bm x_1) f(x2)≥f(x1)+∇f(x1)T(x2−x1)
一阶判别公式证明
必要性
由 f ( x 1 + λ ( x 2 − x 1 ) ) ≤ f ( x 1 ) + λ ( f ( x 2 ) − f ( x 1 ) ) f(x_1+\lambda(x_2-x_1)) \leq f(x_1)+\lambda(f(x_2)-f(x_1)) f(x1+λ(x2−x1))≤f(x1)+λ(f(x2)−f(x1)),得
f ( x 2 ) ≥ f ( x 1 ) + f ( x 1 + λ ( x 2 − x 1 ) ) − f ( x 1 ) λ ( x 2 − x 1 ) ( x 2 − x 1 ) f(x_2)\geq f(x_1)+\frac{f(x_1+\lambda(x_2-x_1))-f(x_1)}{\lambda (x_2-x_1)}(x_2-x_1) f(x2)≥f(x1)+λ(x2−x1)f(x1+λ(x2−x1))−f(x1)(x2−x1)显然当 λ → 0 \lambda \to 0 λ→0时, f ( x 2 ) ≥ f ( x 1 ) + f ′ ( x 1 ) ( x 2 − x 1 ) f(x_2)\geq f(x_1)+f'(x_1)(x_2-x_1) f(x2)≥f(x1)+f′(x1)(x2−x1),必要性得证。
充分性
由 f ( x ) ≥ f ( y ) + f ′ ( y ) ( x − y ) f(x)\geq f(y)+f'(y)(x-y) f(x)≥f(y)+f′(y)(x−y),因此
f ( x 1 ) ≥ f ( y ) + f ′ ( y ) ( x 1 − y ) , f ( x 2 ) ≥ f ( y ) + f ′ ( y ) ( x 2 − y ) f(x_1) \geq f(y)+f'(y)(x_1-y),\quad f(x_2) \geq f(y)+f'(y)(x_2-y) f(x1)≥f(y)+f′(y)(x1−y),f(x2)≥f(y)+f′(y)(x2−y)因此令 y = x 1 + λ ( x 2 − x 1 ) y=x_1+\lambda(x_2-x_1) y=x1+λ(x2−x1),上面左侧不等式两侧乘 ( 1 − λ ) (1-\lambda) (1−λ)、右侧不等式两侧乘 λ \lambda λ,合并两个不等式得
( 1 − λ ) f ( x 1 ) + λ f ( x 2 ) ≥ f ( y ) + f ′ ( y ) [ x 1 + λ ( x 2 − x 1 ) − y ] = f ( y ) (1-\lambda)f(x_1)+\lambda f(x_2) \geq f(y) + f'(y)[x_1+\lambda(x_2-x_1) - y]=f(y) (1−λ)f(x1)+λf(x2)≥f(y)+f′(y)[x1+λ(x2−x1)−y]=f(y)显然 f ( x 1 + λ ( x 2 − x 1 ) ) ≤ f ( x 1 ) + λ ( f ( x 2 ) − f ( x 1 ) ) f(x_1+\lambda(x_2-x_1)) \leq f(x_1)+\lambda(f(x_2)-f(x_1)) f(x1+λ(x2−x1))≤f(x1)+λ(f(x2)−f(x1)),充分性得证。
几何解释: ( x , f ( x ) ) (x, f(x)) (x,f(x))为曲线 f f f上一点, y y y为该点处的切线,则自变量 x x x增加 Δ x \Delta x Δx,对曲线 f f f和切线 y y y带来的变化分别为 Δ f \Delta f Δf和 Δ y \Delta y Δy,则
Δ f > Δ y \Delta f \gt \Delta y Δf>Δy

2.3 二阶判别公式
设 f f f是定义在凸集 S S S上的二阶可微函数,则 f f f为凸函数的充要条件是在任意 x ∈ S \bm x \in S x∈S处,Hesse矩阵半正定。
二阶判别公式证明
必要性
对任一点 x ∗ ∈ S \bm x^* \in S x∗∈S,存在 λ ∈ [ − δ , δ ] \lambda \in [-\delta, \delta] λ∈[−δ,δ],有 x ∗ + λ x ∈ S \bm x^* + \lambda \bm x \in S x∗+λx∈S,因此
f ( x ∗ + λ x ) ≥ f ( x ∗ ) + λ ∇ f ( x ∗ ) T x f(\bm x^* + \lambda \bm x) \geq f(\bm x^*) + \lambda \nabla f(\bm x^*)^T \bm x f(x∗+λx)≥f(x∗)+λ∇f(x∗)Tx由 f ( x ) f(\bm x) f(x)在点 x ∗ \bm x^* x∗处二次可微,则
f ( x ∗ + λ x ) = f ( x ∗ ) + λ ∇ f ( x ∗ ) T x + 1 2 λ 2 x T ∇ 2 f ( x ∗ ) x + o ( ∣ ∣ λ x ∣ ∣ 2 ) f(\bm x^* + \lambda \bm x)=f(\bm x^*) + \lambda \nabla f(\bm x^*)^T \bm x+\frac{1}{2}\lambda^2\bm x^T\nabla^2f(\bm x^*)\bm x + o(||\lambda \bm x||^2) f(x∗+λx)=f(x∗)+λ∇f(x∗)Tx+21λ2xT∇2f(x∗)x+o(∣∣λx∣∣2)故 1 2 λ 2 x T ∇ 2 f ( x ∗ ) x + o ( ∣ ∣ λ x ∣ ∣ 2 ) ≥ 0 \dfrac{1}{2}\lambda^2\bm x^T\nabla^2f(\bm x^*)\bm x + o(||\lambda \bm x||^2)\geq0 21λ2xT∇2f(x∗)x+o(∣∣λx∣∣2)≥0,因此
x T ∇ 2 f ( x ∗ ) x ≥ 0 \bm x^T\nabla^2f(\bm x^*)\bm x \geq 0 xT∇2f(x∗)x≥0即 ∇ 2 f ( x ∗ ) \nabla^2f(\bm x^*) ∇2f(x∗)半正定,必要性得证。
充分性
设Hesse矩阵 ∇ 2 f ( x ) \nabla^2f(\bm x) ∇2f(x)在每一点 x ∈ S \bm x\in S x∈S处半正定,对任意 x ∗ , x ∈ \bm x^*, \bm x\in x∗,x∈ 凸集 S S S,由中值定理得
f ( x ) = f ( x ∗ ) + ∇ f ( x ∗ ) T ( x − x ∗ ) + 1 2 ( x − x ∗ ) 2 ∇ 2 f ( x ^ ) ( x − x ∗ ) f(\bm x) = f(\bm x^*) + \nabla f(\bm x^*)^T(\bm x-\bm x^*)+\frac{1}{2}(\bm x-\bm x^*)^2\nabla^2f(\hat \bm x)(\bm x-\bm x^*) f(x)=f(x∗)+∇f(x∗)T(x−x∗)+21(x−x∗)2∇2f(x^)(x−x∗)其中 x ^ = x + λ ( x ∗ − x ) \hat \bm x=\bm x+\lambda(\bm x^*-\bm x) x^=x+λ(x∗−x),因此当 ∇ 2 f ( x ^ ) \nabla^2f(\hat \bm x) ∇2f(x^)半正定时,必有
( x − x ‾ ) T ∇ 2 f ( x ^ ) ( x − x ‾ ) ≥ 0 (x-\overline x)^T\nabla^2f(\hat x)(x-\overline x)\geq 0 (x−x)T∇2f(x^)(x−x)≥0故 f ( x ) ≥ f ( x ∗ ) + ∇ f ( x ∗ ) T ( x − x ∗ ) f(\bm x) \geq f(\bm x^*) + \nabla f(\bm x^*)^T(\bm x-\bm x^*) f(x)≥f(x∗)+∇f(x∗)T(x−x∗),充分性得证。
3 凸规划
考虑非线性规划问题
min f ( x ) x ∈ R n s.t. g i ( x ) ≤ 0 , i = 1 , ⋯   , m h j ( x ) = 0 , j = 1 , ⋯   , l \begin{aligned} \min &\quad f(\bm{x}) \quad \bm{x}\in\R^n\\ \text{s.t.} &\quad g_i(\bm{x}) \leq 0,\quad i=1,\cdots,m\\ &\quad h_j(\bm{x}) = 0,\quad j=1,\cdots,l\\ \end{aligned} mins.t.f(x)x∈Rngi(x)≤0,i=1,⋯,mhj(x)=0,j=1,⋯,l
设 f ( x ) f(\bm x) f(x)为凸函数, g i ( x ) g_i(\bm x) gi(x)为凸函数, h j ( x ) h_j(\bm x) hj(x)是线性函数,则问题的可行域为
S = { x ∣ g i ( x ) ≥ 0 , i = 1 , ⋯   , m ; h j ( x ) = 0 , j = 1 , ⋯   , l } S = \{ \bm x\ |\ g_i(\bm x)\geq 0, i= 1,\cdots, m;\ h_j(\bm x)=0, j = 1,\cdots,l\} S={x ∣ gi(x)≥0,i=1,⋯,m; hj(x)=0,j=1,⋯,l}
上述问题是求凸函数在凸集上的极小点,这类问题成为凸规划。
重要性质:凸规划的局部极小点就是全局极小点,证明见2.1。
这篇关于凸集、凸函数与凸规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!