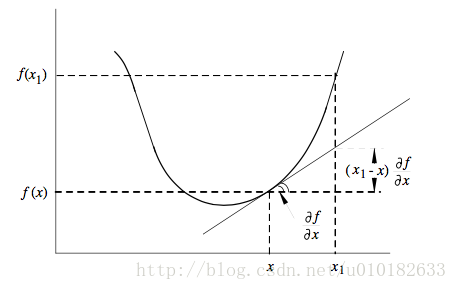
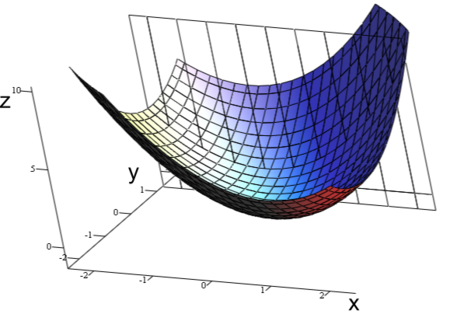
凸函数专题

组合优化与凸优化学习笔记3 凸函数

目前学到了73页凸函数的定义：人话：函数f的定义域是凸集（在一般的情况下就是不能是断开的定义域（一般的情况是1维的嘛），假如x是什么多维向量的话就是说x的取值范围是一个凸集内），并且还满足3.1式子，那么这个函数就叫凸函数。一般来说凸函数都长这个样子：毕竟在3.1式子中可以看到右边的式子其实就是x,y之间的凸集（也就是它们之间的线段）而左边是实际的函数值，函数值要小当然就长

凸函数的局部最优也是全局最优的证明

这个性质早就知道了，但并不太清楚严谨的证明是什么。这也是《Introduction to linear optimization》书中第三章课后题的第一题。这篇博客给出严谨的证明。 Exercise 3.1 (Local minimum of convex functions) Let f : R n → R f: \mathcal{R}^n \rightarrow \mathcal{R}

用c++用4个凸函数（觉得啥好用用啥）去测试adam，rmsprop，adagrad算法的性能（谁先找到最优点）

为了测试 Adam、RMSProp 和 Adagrad 算法的性能，你可以使用四个凸函数进行实验。以下是一些常用的凸函数示例： Rosenbrock 函数： Booth 函数： Himmelblau 函数： Beale 函数：你可以选择其中一个或多个函数来测试算法的性能。对于每个函数，你可以使用不同的初始点，并应用 Adam、RMSProp 和 Adagrad 算法来寻找最优

凹函数和凸函数

同济高数上册，第三章，第四节，p147 切勿把定义看死了！！！真实的情况是：向上凸的就是向下凹的，向上凹的就是向下凸的。教材中选定了向上为正方向，所以要辩证的来看定义。

漫步凸分析四——凸函数

令函数 f f的值域是实数或±∞\pm\infty，定义域是 Rn R^n的一个子集，集合 {(x,μ)|x∈S,μ∈R,μ≥f(x)} \{(x,\mu)|x\in S,\mu\in R,\mu\geq f(x)\} 叫做 f f的上境图(epigraph)，用epiff表示，如果epi f f是Rn+1R^{n+1}的凸子集，那么我们将 f f定义为凸函数。对于SS 上

漫步最优化十四——凸函数与凹函数

我一直都在流浪， \textbf{我一直都在流浪，} 可我却不曾见过海洋。 \textbf{可我却不曾见过海洋。} 我努力微笑坚强， \textbf{ 我努力微笑坚强，} 用寂寞筑成一道围墙。 \textbf{用寂寞筑成一道围墙。} 如果恨你，就没发忘记你， \textbf{如果恨你，就没发忘记你，} 如果不够悲伤，就无法飞翔。 \textbf{如果不够

凸规划理论——计算几何，凸集，超平面，凸函数，凸规划判别

文章目录一、计算几何是研究什么的？二、计算几何理论中（或凸集中）过两点的一条直线的表达式，是如何描述的？与初中数学中那些直线方程有什么差异？三、凸集是什么？直线是凸集吗？是仿射集吗？四、三维空间中的一个平面，如何表达？五、更高维度的“超平面”，如何表达？六、什么是“凸函数”定义？什么是Hessen矩阵? 如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？1.凸函数的定义2.He

凸函数成立的一阶与二阶条件

文章目录 1、凸函数成立的一阶条件2、凸函数成立的二阶条件本文主要是针对凸函数成立的一阶和二阶充要条件进行描述和简单证明。 1、凸函数成立的一阶条件【定理1】对于函数 J : Ω → R J:\Omega \rightarrow \mathbb{R} J:Ω→R， J J J为凸函数，当且仅当 ∀ x , y ∈ Ω \forall \bf{x},\bf{y}\i

凸集、凸函数与凸规划

文章目录 1 凸集2 凸函数2.1 凸函数性质2.2 一阶判别公式2.3 二阶判别公式 3 凸规划 1 凸集设集合 S ⊂ R n S\subset \R^n S⊂Rn，若 S S S中任意两点连线仍属于 S S S，则 S S S称为凸集，即 x 1 + λ ( x 2 − x 1 ) ∈ S \bm x_1 + \lambda(\bm x_2 - \bm x_1) \

凸函数笔记（1）

目录 1. 凸函数基本概念2.可微函数的凸性判定2.1 函数凸性的微分判据2.2 可微凸函数的例子 3. 保凸运算3.1 复合函数的凸性3.2 几种保凸运算 1. 凸函数基本概念记 R ‾ : = R ∪ { ± ∞ } . 对函数 f : R n → R ‾ , 称记\overline{\mathbb{R}}:=\mathbb{R}\cup\{\pm\infty\}.

非凸函数上，随机梯度下降能否收敛？网友热议：能，但有条件，且比凸函数收敛更难

非凸函数上，随机梯度下降能否收敛？网友热议：能，但有条件，且比凸函数收敛更难机器学习研究组订阅 2022-02-07 18:16 非凸优化问题被认为是非常难求解的，因为可行域集合可能存在无数个局部最优点，通常求解全局最优的算法复杂度是指数级的（NP 困难）。那么随机梯度下降能否收敛于非凸函数？针对这一问题，众多网友进行了一番讨论。在机器学习领域，我们经常会听到凸函数和非凸函数

“凸函数”是什么？

凸函数（英文：Convex function）是指函数图形上，任意两点连成的线段，皆位于图形的上方，如单变数的二次函数和指数函数。二阶可导的一元函数为凸，当且仅当其定义域为凸集，且函数的二阶导数″在整个定义域上非负。直观理解，凸函数的图像形如开口向上的杯∪，而相反，凹函数则形如开口向下的帽∩。在最优化研究中，凸函数的最小化问题有唯一性，即凸开集上的严格凸函数，至多只有一个极小值。凸函数

Convex Set and Convex Function凸集与凸函数

Welcome To My Blog Rockafeller说:”优化问题的分水岭不是线性和非线性,而是凸性和非凸性” 两点连线上的点在介绍凸集和凸函数之前,先来看一个与之有关的基本问题: 如下图,已知空间中有B,C两点,在给定两点坐标的情况下如何量化B,C连线上的任意一点D? 很简单,看下图,设已知A,B,C,D的坐标, AD = AB + BD = AB + kBC (D在

凸优化基础之计算几何、凸集、凸函数、凸规划

目录一、计算几何1.什么是计算几何2.计算几何理论中过两点的一条直线的表达式，是如何描述的？二、凸集1.什么是凸集2.如何表达三维空间中的一个平面3.如何表达超平面4.什么是凸函数及如何判别5.什么是凸规划及如何判别一、计算几何 1.什么是计算几何计算几何是计算机理论科学的一个重要分支.自20世纪70年代末从算法设计与分析中独立出来起，不到30年，该学科已经有了巨大的

凸优化面试题：凸集凸函数凸优化

为什么研究凸优化先要从凸集的性质开始：凸函数图像的上方区域，一定是凸集；假如一个函数上方是凸集，这个函数就是凸函数如何用向量表示几何体什么是凸包包含凸集的最小集合如何计算一个凸集的凸包是什么？时间复杂度是多少转化为排序问题，时间复杂度是nlogn 凸集基本概念

凸数据集与凸函数

凸数据集与凸函数凸数据集凸函数定义判定方法凸数据集如果一个数据集D是凸的，那么对于其中任意的两点x,y∈D，θ∈R,0≤θ≤1, 则 θ x + ( 1 − θ ) y ∈ D 表达式θx+(1−θ)y被称作点x , y 的凸性组合(convex combination) 通俗的讲，就是数据集D中任意两点的连线上的点，也在数据集D内，那么数据集D就是一个凸集。如下图

$怎么理解二阶偏导与凸函数的Hessian矩阵是半正定的？$

怎么理解二阶偏导与凸函数的Hessian矩阵是半正定的？

转载出处：https://www.zhihu.com/question/40181086?sort=created 教科书上有严格的证明，这个答案试图通过类比来提供一些直观上的理解。大概的结论是，多元函数的Hessian矩阵就类似一元函数的二阶导。多元函数Hessian矩阵半正定就相当于一元函数二阶导非负，半负定就相当于一元函数二阶导非正。如果这个类比成立的话，凸函数的Hessian