“凸函数”是什么？

2023-11-05 10:04

文章标签 凸函数

本文主要是介绍“凸函数”是什么？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

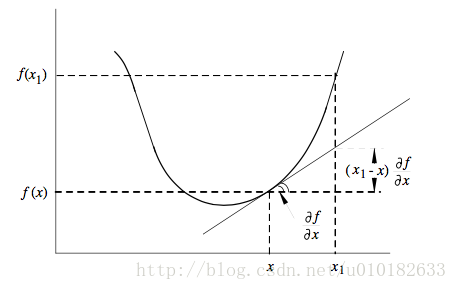
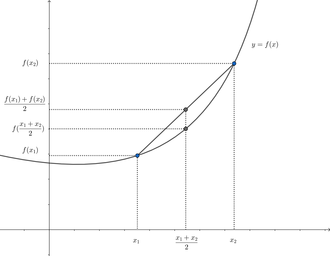
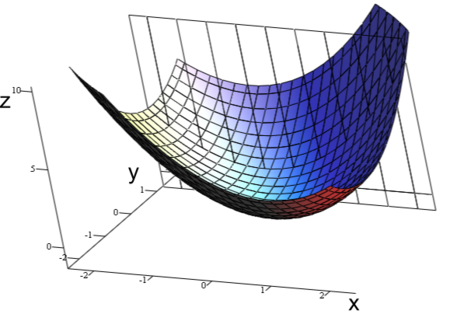
凸函数（英文：Convex function）是指函数图形上，任意两点连成的线段，皆位于图形的上方，如单变数的二次函数和指数函数。二阶可导的一元函数为凸，当且仅当其定义域为凸集，且函数的二阶导数″在整个定义域上非负。直观理解，凸函数的图像形如开口向上的杯∪，而相反，凹函数则形如开口向下的帽∩。在最优化研究中，凸函数的最小化问题有唯一性，即凸开集上的严格凸函数，至多只有一个极小值。

凸函数的图像上任取两点，连成的线段必在图像上方。

二元二次多项式函数(的图像，形如开口向上的碗。

https://zh.wikipedia.org/zh-hans/%E5%87%B8%E5%87%BD%E6%95%B0

这篇关于“凸函数”是什么？的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/349115。 23002807@qq.com

相关文章

组合优化与凸优化学习笔记3 凸函数

组合优化与凸优化学习笔记3 凸函数

目前学到了73页凸函数的定义：人话：函数f的定义域是凸集（在一般的情况下就是不能是断开的定义域（一般的情况是1维的嘛），假如x是什么多维向量的话就是说x的取值范围是一个凸集内），并且还满足3.1式子，那么这个函数就叫凸函数。一般来说凸函数都长这个样子：毕竟在3.1式子中可以看到右边的式子其实就是x,y之间的凸集（也就是它们之间的线段）而左边是实际的函数值，函数值要小当然就长

阅读更多...

凸函数的局部最优也是全局最优的证明

凸函数的局部最优也是全局最优的证明

这个性质早就知道了，但并不太清楚严谨的证明是什么。这也是《Introduction to linear optimization》书中第三章课后题的第一题。这篇博客给出严谨的证明。 Exercise 3.1 (Local minimum of convex functions) Let f : R n → R f: \mathcal{R}^n \rightarrow \mathcal{R}

阅读更多...

用c++用4个凸函数（觉得啥好用用啥）去测试adam，rmsprop，adagrad算法的性能（谁先找到最优点）

用c++用4个凸函数（觉得啥好用用啥）去测试adam，rmsprop，adagrad算法的性能（谁先找到最优点）

为了测试 Adam、RMSProp 和 Adagrad 算法的性能，你可以使用四个凸函数进行实验。以下是一些常用的凸函数示例： Rosenbrock 函数： Booth 函数： Himmelblau 函数： Beale 函数：你可以选择其中一个或多个函数来测试算法的性能。对于每个函数，你可以使用不同的初始点，并应用 Adam、RMSProp 和 Adagrad 算法来寻找最优

阅读更多...

凹函数和凸函数

凹函数和凸函数

同济高数上册，第三章，第四节，p147 切勿把定义看死了！！！真实的情况是：向上凸的就是向下凹的，向上凹的就是向下凸的。教材中选定了向上为正方向，所以要辩证的来看定义。

阅读更多...

漫步凸分析四——凸函数

漫步凸分析四——凸函数

令函数 f f的值域是实数或±∞\pm\infty，定义域是 Rn R^n的一个子集，集合 {(x,μ)|x∈S,μ∈R,μ≥f(x)} \{(x,\mu)|x\in S,\mu\in R,\mu\geq f(x)\} 叫做 f f的上境图(epigraph)，用epiff表示，如果epi f f是Rn+1R^{n+1}的凸子集，那么我们将 f f定义为凸函数。对于SS 上

阅读更多...

漫步最优化十四——凸函数与凹函数

漫步最优化十四——凸函数与凹函数

我一直都在流浪， \textbf{我一直都在流浪，} 可我却不曾见过海洋。 \textbf{可我却不曾见过海洋。} 我努力微笑坚强， \textbf{ 我努力微笑坚强，} 用寂寞筑成一道围墙。 \textbf{用寂寞筑成一道围墙。} 如果恨你，就没发忘记你， \textbf{如果恨你，就没发忘记你，} 如果不够悲伤，就无法飞翔。 \textbf{如果不够

阅读更多...

凸规划理论——计算几何，凸集，超平面，凸函数，凸规划判别

凸规划理论——计算几何，凸集，超平面，凸函数，凸规划判别

文章目录一、计算几何是研究什么的？二、计算几何理论中（或凸集中）过两点的一条直线的表达式，是如何描述的？与初中数学中那些直线方程有什么差异？三、凸集是什么？直线是凸集吗？是仿射集吗？四、三维空间中的一个平面，如何表达？五、更高维度的“超平面”，如何表达？六、什么是“凸函数”定义？什么是Hessen矩阵? 如何判别一个函数是凸函数？f(x)=x^3 函数是凸函数吗？1.凸函数的定义2.He

阅读更多...

凸函数成立的一阶与二阶条件

凸函数成立的一阶与二阶条件

文章目录 1、凸函数成立的一阶条件2、凸函数成立的二阶条件本文主要是针对凸函数成立的一阶和二阶充要条件进行描述和简单证明。 1、凸函数成立的一阶条件【定理1】对于函数 J : Ω → R J:\Omega \rightarrow \mathbb{R} J:Ω→R， J J J为凸函数，当且仅当 ∀ x , y ∈ Ω \forall \bf{x},\bf{y}\i

阅读更多...

凸集、凸函数与凸规划

凸集、凸函数与凸规划

文章目录 1 凸集2 凸函数2.1 凸函数性质2.2 一阶判别公式2.3 二阶判别公式 3 凸规划 1 凸集设集合 S ⊂ R n S\subset \R^n S⊂Rn，若 S S S中任意两点连线仍属于 S S S，则 S S S称为凸集，即 x 1 + λ ( x 2 − x 1 ) ∈ S \bm x_1 + \lambda(\bm x_2 - \bm x_1) \

阅读更多...

凸函数笔记（1）

凸函数笔记（1）

目录 1. 凸函数基本概念2.可微函数的凸性判定2.1 函数凸性的微分判据2.2 可微凸函数的例子 3. 保凸运算3.1 复合函数的凸性3.2 几种保凸运算 1. 凸函数基本概念记 R ‾ : = R ∪ { ± ∞ } . 对函数 f : R n → R ‾ , 称记\overline{\mathbb{R}}:=\mathbb{R}\cup\{\pm\infty\}.

阅读更多...