漫步最优化十四——凸函数与凹函数

本文主要是介绍漫步最优化十四——凸函数与凹函数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

我一直都在流浪， $\textbf{我一直都在流浪，}$

可我却不曾见过海洋。 $\textbf{可我却不曾见过海洋。}$

我努力微笑坚强， $\textbf{ 我努力微笑坚强，}$

用寂寞筑成一道围墙。 $\textbf{用寂寞筑成一道围墙。}$

如果恨你，就没发忘记你， $\textbf{如果恨你，就没发忘记你，}$

如果不够悲伤，就无法飞翔。 $\textbf{如果不够悲伤，就无法飞翔。}$

那就让我孤独到底，直到忘记了呼吸。 $\textbf{那就让我孤独到底，直到忘记了呼吸。}$

——畅宝宝的傻逼哥哥 $\qquad\qquad\quad\textbf{——畅宝宝的傻逼哥哥}$

通常在实际中，最小化的函数有几个极值，所以最优化算法得出的极值不确实是否为全局的极值，对于一些特殊的函数，凸函数与凹函数，任何局部极值也是全局极致，因此如果目标函数是凸的或凹的，那么优化算法就能保证是全局的。

$\textbf{定义1：}$ 集合 $R_c\subset E^n$ 是凸集，如果对每对点 $\textbf{x}_1,\textbf{x}_2\subset R_c$ ，每个实数 $\alpha,0<\alpha<1$ ，点

x = α x 1 + (1 - α) x 2

$\textbf{x}=\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2$

位于 $R_c$ ，即 $\textbf{x}\in R_c$ 。

效果上，如果任何两点 $\textbf{x}_1,\textbf{x}_2\in R_c$ 用直线相连， $\textbf{x}_1,\textbf{x}_2$ 之间线上的每个点都在 $R_c$ 中，那么 $R_c$ 是凸的。如果存在点不在 $R_c$ 中，那么该集合是非凸的，凸集合如图1所示。

凸的概念也可以用到函数上。

$\textbf{定义2：}$

我们称定义在凸集 $R_c$ 上的函数 $f(\textbf{x})$ 为凸的，如果对每对 $\textbf{x}_1,\textbf{x}_2\in R_c$ 与每个实数 $\alpha,0<\alpha<1$ ，不等式
$f [α x 1 + (1 - α) x 2] \leq α f (x 1) + (1 - α) f (x 2)$ $f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2]\leq\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2)$

满足。如果 $\textbf{x}_1\neq\textbf{x}_2$

f [α x 1 + (1 - α) x 2] < α f (x 1) + (1 - α) f (x 2)

$f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2]<\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2)$

满足，那么 $f(\textbf{x})$ 是严格凸的。

如果 $\varphi(\textbf{x})$ 定义在凸集 $R_c$ 上且 $f(\textbf{x})=-\varphi(\textbf{x})$ 是凸的，那么 $\varphi(\textbf{x})$ 是凹的。如果 $f(\textbf{x})$ 是严格凸的，那么 $\varphi(\textbf{x})$ 是严格凹的。

上述定义中的不等式，左边是点 $\textbf{x}_1,\textbf{x}_2$ 之间某处的 $f(\textbf{x})$ 值，而右边是基于线性插值得到的 $f(\textbf{x})$ 的近似，因此如果任何两点的线性插值大于函数的值，那么该函数就是凸的，图2a，b中的函数为凸的，2c为非凸的。

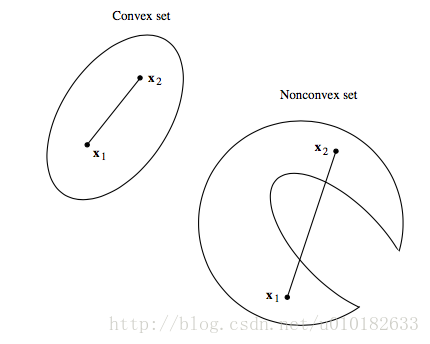
图1

$\textbf{定理1：}$ 如果

f (x) = a f 1 (x) + b f 2 (x)

$f(\textbf{x})=af_1(\textbf{x})+bf_2(\textbf{x})$

其中 $a,b\geq 0,f_1(\textbf{x}),f_2(\textbf{x})$ 是凸集 $R_c$ 上的凸函数，那么 $f(\textbf{x})$ 是集合 $R_c$ 上的凸函数。

$\textbf{证明：}$ 因为 $f_1(\textbf{x}),f_2(\textbf{x})$ 是凸函数， $a,b\geq 0$ ，所以对于 $\textbf{x}=\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2$ ，我们有

a f 1 (α x 1 + (1 - α) x 2) \leq a [α f 1 ((x) 1) + (1 - α) f 1 (x 2)] b f 2 (α x 1 + (1 - α) x 2) \leq b [α f 2 ((x) 1) + (1 - α) f 2 (x 2)]

$\begin{align*} af_1(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2)\leq a[\alpha f_1(\textbf(x)_1)+(1-\alpha)f_1(\textbf{x}_2)]\\ bf_2(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2)\leq b[\alpha f_2(\textbf(x)_1)+(1-\alpha)f_2(\textbf{x}_2)] \end{align*}$

其中 $0<\alpha<1$ ，因此

f (x) f (α x 1 + (1 - α) x 2) = a f 1 (x) + b f 2 (x) = a f 1 (α x 1 + (1 - α) x 2) + b f 2 (α x 1 + (1 - α) x 2) \leq α [a f 1 (x 1) + b f 2 (x 1)] + (1 - α) [a f 1 (x 2) + b f 2 (x 2)]

$\begin{align*} f(\textbf{x})&=af_1(\textbf{x})+bf_2(\textbf{x})\\ f(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2)&=af_1(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2)+bf_2(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2)\\ &\leq\alpha[af_1(\textbf{x}_1)+bf_2(\textbf{x}_1)]+(1-\alpha)[af_1(\textbf{x}_2)+bf_2(\textbf{x}_2)] \end{align*}$

因为

a f 1 (x 1) + b f 2 (x 1) = f (x 1) a f 1 (x 2) + b f 2 (x 2) = f (x 2)

$\begin{align*} af_1(\textbf{x}_1)+bf_2(\textbf{x}_1)=f(\textbf{x}_1)\\ af_1(\textbf{x}_2)+bf_2(\textbf{x}_2)=f(\textbf{x}_2) \end{align*}$

所以上面的不等式可以写成

f (α x 1 + (1 - α) x 2) \leq α f (x 1) + (1 - α) f (x 2)

$f(\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2)\leq\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2)$

即 $f(\textbf{x})$ 是凸函数。

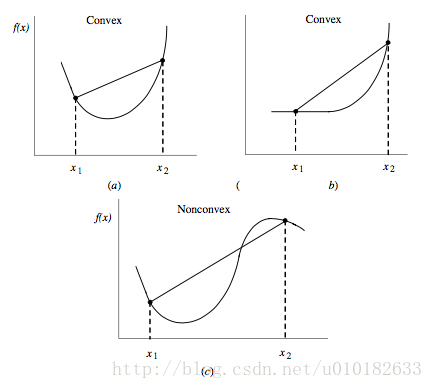
图2

$\textbf{定理2：}$ 如果 $f(\textbf{x})$ 是凸集 $R_c$ 上的凸函数，那么对每个实数 $K$ 而言，集合

S c = {x : x \in R c, f (x) \leq K}

$S_c=\{\textbf{x}:\textbf{x}\in R_c,f(\textbf{x})\leq K\}$

都是凸集。

$\textbf{证明：}$ 如果 $\textbf{x}_1,\textbf{x}_2\in S_c$ ，那么根据 $S_c$ 的定义， $f(\textbf{x}_1)\leq K,f(\textbf{x}_2)\leq K$ ，因为 $f(\textbf{x})$ 是凸集，所以

f [α x 1 + (1 - α) x 2] \leq α f (x 1) + (1 - α) f (x 2) \leq α K + (1 - α) K

$\begin{align*} f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2] &\leq\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2)\\ &\leq\alpha K+(1-\alpha)K \end{align*}$

或者

f (x) \leq K f o r x = α x 1 + (1 - α) x 2 a n d 0 < α < 1

$f(\textbf{x})\leq K\quad for\ \textbf{x}=\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2\quad and\quad 0<\alpha<1$

所以

x \in S c

$\textbf{x}\in S_c$

即 $S_c$ 是凸的。

定理2的图示如图3，其中集合 $S_c$ 是凸集，如果 $f(\textbf{x})$ 在凸集 $R_c$ 上是凸函数的话。

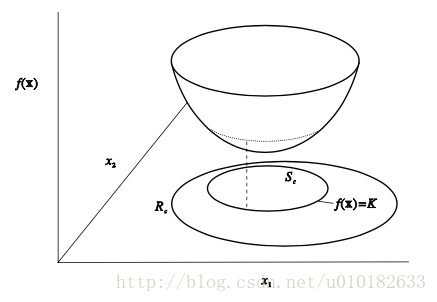
图3

另一种考虑凸的角度是测试 $f(\textbf{x})$ 的梯度与海森矩阵。

$\textbf{定理3：}$ 如果 $f(\textbf{x})\in C^1$ ，那么 $f(\textbf{x})$ 在凸集 $R_c$ 上是凸函数，当且仅当对所有 $\textbf{x},\textbf{x}_1\in R_c$

f (x 1) \geq f (x) + g (x) T (x 1 - x)

$f(\textbf{x}_1)\geq f(\textbf{x})+\textbf{g}(\textbf{x})^T(\textbf{x}_1-\textbf{x})$

其中 $\textbf{g}(\textbf{x})$ 是 $f(\textbf{x})$ 的梯度。

$\textbf{证明：}$ 这个定理的证明由两部分组成。首先我们证明如果 $f(\textbf{x})$ 是凸函数，那么不等式成立。然后证明如果不等式成立，那么 $f(\textbf{x})$ 是凸函数。首先如果 $f(\textbf{x})$ 是凸函数，那么对于所有 $\alpha,0<\alpha<1$

f [α x 1 + (1 - α) x] \leq α f (x 1) + (1 - α) f (x)

$f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}]\leq\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x})\\$

或者

f [x + α (x 1 - x)] - f (x) \leq α [f (x 1) - f (x)]

$f[\textbf{x}+\alpha(\textbf{x}_1-\textbf{x})]-f(\textbf{x})\leq\alpha[f(\textbf{x}_1)-f(\textbf{x})]\\$

当 $\alpha\to 0$ ，由 $f[\textbf{x}+\alpha(\textbf{x}_1-\textbf{x})]$ 的泰勒级数可得

f (x) + g (x) T α (x 1 - x) - f (x) \leq α [f (x 1) - f (x)]

$f(\textbf{x})+\textbf{g}(\textbf{x})^T\alpha(\textbf{x}_1-\textbf{x})-f(\textbf{x})\leq\alpha[f(\textbf{x}_1)-f(\textbf{x})]\\$

所以

f (x 1) \geq f (x) + g (x) T (x 1 - x)

$f(\textbf{x}_1)\geq f(\textbf{x})+\textbf{g}(\textbf{x})^T(\textbf{x}_1-\textbf{x})$

接下来，如果不等式在 $\textbf{x},\textbf{x}_2\in R_c$ 处成立，那么

f (x 2) \geq f (x) + g (x) T (x 2 - x)

$f(\textbf{x}_2)\geq f(\textbf{x})+\textbf{g}(\textbf{x})^T(\textbf{x}_2-\textbf{x})$

从上面两式可得

α f (x 1) + (1 - α) f (x 2) \geq α f (x) + α g (x) T (x 1 - x) + (1 - α) f (x) + (1 - α) g (x) T (x 2 - x)

$\begin{align*} \alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2) &\geq\alpha f(\textbf{x})+\alpha\textbf{g}(\textbf{x})^T(\textbf{x}_1-\textbf{x})+(1-\alpha)f(\textbf{x})\\ &+(1-\alpha)\textbf{g}(\textbf{x})^T(\textbf{x}_2-\textbf{x}) \end{align*}$

或者

α f (x 1) + (1 - α) f (x 2) \geq f (x) + g T (x) [α x 1 + (1 - α) x 2 - x]

$\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2)\geq f(\textbf{x})+\textbf{g}^T(\textbf{x})[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2-\textbf{x}]$

代入

x = α x 1 + (1 - α) x 2

$\textbf{x}=\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2$

可得

f [α x 1 + (1 - α) x 2] \leq α f (x 1) + (1 - α) f (x 2)

$f[\alpha\textbf{x}_1+(1-\alpha)\textbf{x}_2]\leq\alpha f(\textbf{x}_1)+(1-\alpha)f(\textbf{x}_2)$

其中 $0<\alpha<1$ ，因此 $f(\textbf{x})$ 是凸函数。

定理3说明 $f(\textbf{x})$ 在点 $\textbf{x}$ 处基于 $f(\textbf{x})$ 导数的线性插值小于函数值，如图4所示。

$\textbf{定理4：}$ 函数 $f(\textbf{x})\in C^2$ 是凸集 $R_c$ 上的凸函数，当且仅当 $f(\textbf{x})$ 的海森矩阵 $H(\textbf{x})$ 对 $\textbf{x}\in R_c$ 是半正定的。

$\textbf{证明：}$ 如果 $\textbf{x}_1=\textbf{x+d}$ ，其中 $\textbf{x}_1,\textbf{x}$ 是 $R_c$ 中的任意点，那么由泰勒级数可得

f (x 1) = f (x) + g T (x) (x 1 - x) + 1 2 d T H (x + α d) d

$f(\textbf{x}_1)=f(\textbf{x})+\textbf{g}^T(\textbf{x})(\textbf{x}_1-\textbf{x})+\frac{1}{2}\textbf{d}^T\textbf{H}(\textbf{x}+\alpha\textbf{d})\textbf{d}$

其中 $0\leq\alpha\leq 1$ ，接下来如果 $\textbf{H}(\textbf{x})$ 在 $R_c$ 中是半正定的，那么

1 2 d T H (x + α d) d \geq 0

$\frac{1}{2}\textbf{d}^T\textbf{H}(\textbf{x}+\alpha\textbf{d})\textbf{d}\geq 0$

所以

f (x 1) \geq f (x) + g T (x) (x 1 - x)

$f(\textbf{x}_1)\geq f(\textbf{x})+\textbf{g}^T(\textbf{x})(\textbf{x}_1-\textbf{x})$

所以由定理3可知 $f(\textbf{x})$ 是凸函数。

如果 $\textbf{H}(\textbf{x})$ 在 $R_c$ 任何处都是半正定的，那么存在点 $\textbf{x}$ 与方向 $\textbf{d}$ 使得

d T H (x + α d) < 0

$\textbf{d}^T\textbf{H}(\textbf{x}+\alpha\textbf{d})<0$

所以

f (x 1) < f (x) + g T (x) (x 1 - x)

$f(\textbf{x}_1)<f(\textbf{x})+\textbf{g}^T(\textbf{x})(\textbf{x}_1-\textbf{x})$

根据定理3可知 $f(\textbf{x})$ 是非凸的，所以当且仅当 $\textbf{H}(\textbf{x})$ 在 $R_c$ 任何地方是半正定时 $f(\textbf{x})$ 是凸函数。

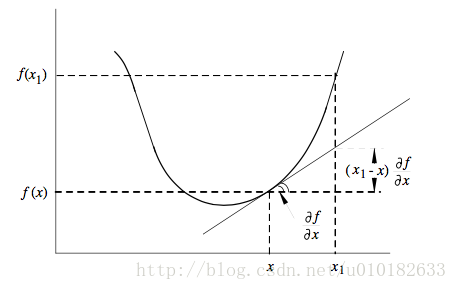
图4

对于严格凸函数，上面的定理修改如下：

$\textbf{定理5：}$

如果 $f(\textbf{x})$ 是凸集 $R_c$ 上的严格凸函数，那么对每个实数 $K$ 而言，集合
$S c = {x : x \in R c, f (x) < K}$ $S_c=\{\textbf{x}:\textbf{x}\in R_c,f(\textbf{x})<K\}$

都是凸集。

如果 $f(\textbf{x})\in C^1$ ，那么 $f(\textbf{x})$ 在凸集 $R_c$ 上的严格凸函数，当且仅当对所有 $\textbf{x},\textbf{x}_1\in R_c$
$f (x 1) > f (x) + g (x) T (x 1 - x)$ $f(\textbf{x}_1)>f(\textbf{x})+\textbf{g}(\textbf{x})^T(\textbf{x}_1-\textbf{x})$

其中 $\textbf{g}(\textbf{x})$ 是 $f(\textbf{x})$ 的梯度。

函数 $f(\textbf{x})\in C^2$ 是凸集 $R_c$ 上的凸函数，当且仅当 $f(\textbf{x})$ 的海森矩阵 $H(\textbf{x})$ 对 $\textbf{x}\in R_c$ 是正定的。

如果 $\varphi(\textbf{x})$ 定义在凸集 $R_c$ 上，且 $f(\textbf{x})=-\varphi(\textbf{x})$ 是严格凸函数，那么 $\varphi(\textbf{x})$ 是严格凹函数且其海森矩阵是负定的。反过来，如果 $\varphi(\textbf{x})$ 的海森矩阵是负定的，那么 $\varphi(\textbf{x})$ 是严格凹的。