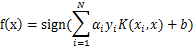最优化专题
[最优化方法] 《最优化方法》个人问答式学习笔记 with LLM
《最优化方法》问答式学习笔记 with LLM 文章目录 《最优化方法》问答式学习笔记 with LLM写在前面每周提问的链接表格绪论 | 第一周 | [answer by 文心一言]Q1 请为我解释一下最优化方法研究的核心重点主要是哪些?一、问题定义与建模二、求解方法三、算法性能与优化四、应用领域与交叉学科 Q2 请为我分别解释一下L0,L1和L2范数。L0范数L1范数L2范数总结 Q3
最优化方法Python计算:一般凸二次规划的有效集算法
先考虑仅含不等式约束的二次规划 { minimize 1 2 x ⊤ H x + c ⊤ x s.t. A x ≥ b . ( 1 ) \begin{cases} \text{minimize}\quad \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Hx}+\boldsymbol{c}^\top\boldsymbol{x}\\ \text{s.t.\
最优化方法Python计算:二次规划的拉格朗日算法
目标函数为二次式,约束条件为线性式的最优化问题称为二次规划。其一般形式为 { minimize 1 2 x ⊤ H x + c ⊤ x s.t. A e q x − b e q = o A i q x − b i q ≥ o . \begin{cases} \text{minimize}\quad \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Hx}+\
压缩感知之最优化研究现状
原文链接:http://blog.sciencenet.cn/blog-497160-388963.html Nyquist属于 local采样方式,其对应的信号重建算法是线性的; CS采用global的非自适应测量方式,从而大大减少数据采集量,然而其付出的代价是信号的重建算法的软件成本。因此,CS的最优化算法好坏直接影响到CS理论能否实用。 区别于Nyquist理论的线性感知问题
Lecture3——线性最优化(Linear Optimization)
一,本文重点 线性最优化(LP)和标准线性最优化(Standard LP form)的定义如何将LP转换为Standard LP用Python解决LP问题将非线性最优化问题(NLP)转换为LP 二,定义 1,线性最优化 定义 线性最优化问题,或者线性规划(linear programming,缩写:LP)是一个目标函数和所有限制函数(在决策变量中)都是线性的最优化问题。 注意:
Lecture2——最优化问题建模
一,建模 1,重要性 实际上,我们并没有得到一个数学公式——通常问题是由某个领域的专家口头描述的。能够将问题转换成数学公式非常重要。建模并不是一件容易的事:有时,我们不仅想找到一个公式,还想找到一个好的公式。找到一个好的优化模型至少是解决问题的一半。 2,建模的一般步骤 分辨信息是否已知:已知为参数(parameter),未知为决策变量。分辨决策变量分辨任务目标:我们要实现什么?(目标
利用 AI 深度学习,实现化合物配比最优化解决方案
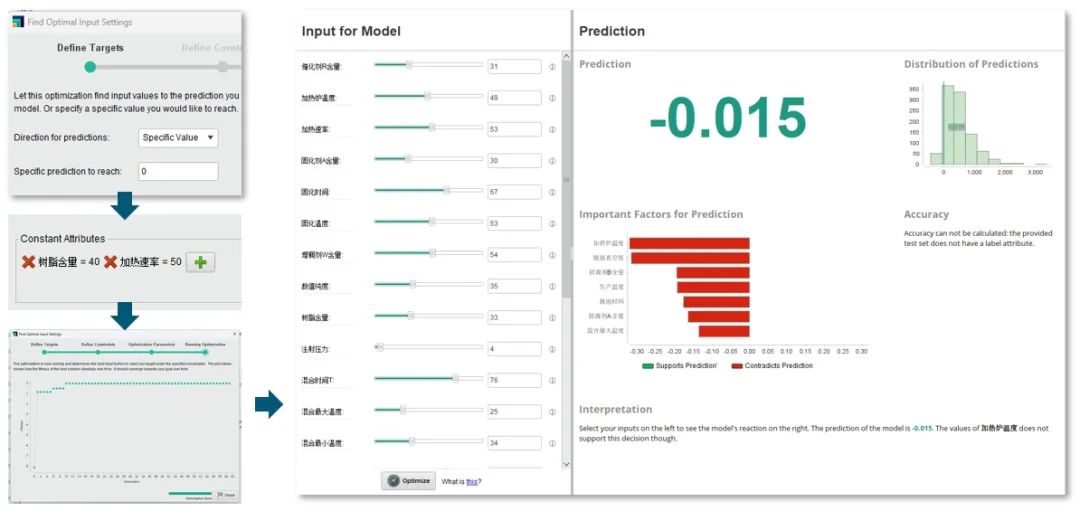
为什么需要化合物配比的优化? 在化合物制造行业中,化合物的配比是产品质量控制的关键环节。 化合物制造流程 目前,这一过程高度依赖于材料专家和工程技术人员的经验,通过反复试验来验证产品性能,确保其满足市场和客户的要求。然而,这种传统的试错方法存在着显著的局限性,包括周期长、成本高,无法保证每次都能找到最接近的配比方案。 如何利用AI方案进行优化? 利用AI技
【最优化方法】实验二 一维搜索方法的MATLAB实现
实验二 一维搜索方法的MATLAB实现 实验的目的和要求:通过本次实验应使学生掌握如何使用MATLAB软件进行一维搜索,并学会对具体问题进行分析。 实验内容: 1、0.618法的MATLAB实现 2、Fibonacci法的MATLAB实现 学习建议: 本次实验是学生初次使用MATLAB进行优化问题的实验,本次实验就是要通过对一些具体问题的分析学会软件的操作并加深对理论知识的理解。
【matlab基础知识代码】(十八)无约束最优化问题
min下面的x称为优化向量或者是决策变量 匿名函数法 >> f=@(x)(x(1)^2-2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2)); x0=[0; 0]; [x,b,c,d]=fminsearch(f,x0), x = 0.6111 -0.3056 b = -0.6414 c = 1 d =
AI理论随笔-最优化(4)
单纯形法(1): 以下列规划问题为例: m a x z = 12 x 4 + 5 x 5 s . t . { x 1 + x 2 + x 3 + x 4 + x 5 = 17 2 x 1 + 3 x 2 + x 3 + 7 x 4 + 4 x 5 = 18 x 2 + x 3 + 3 x 4 + 4 x 5 = 6 5 x 1 + 4 x 2 + x 3 + 5 x 4 − 2 x 5 =
AI理论随笔-最优化(3)
非齐次方程组 A X = b AX=b AX=b求解。 可设前r列线性无关。 ( A : b ) 行 变 换 → [ c 11 c 12 . . . . . . d 1 c 22 . . . . . . d 2 . . . d 2 c r r . . . d r d r + 1 . . . . . . ] (A:b)\underrightarrow{行变换} \begin{bmatrix} c_
AI理论随笔-最优化(2)
齐次线性方程组的解集的极大线性无关组称为该齐次线性方程组的基础解系。基础解系是线性无关的,简单的理解就是能够用它的线性组合表示出该方程组的任意一组解。 基础解系不是唯一的,因为基础解系是AX=0的所有解的极大无关组。也是AX=0解空间的基基也不是唯一的。 基础解系针对齐次线性方程组 A X = 0 AX = 0 AX=0而言的. 当 r ( A ) ≤ n r(A)\leq n r(A)≤n
AI理论随笔-最优化(1)
线性规则(优化)是一类最优化问题。其中,目标函数是未知数的线性函数。约束条件是线性等式和线性不等式构成。 标准形式为: m i n ( m a x ) c T x s . t . A x = b x ≥ 0 min(max) c^{T}x\\ s.t.Ax=b\\ x\geq0 min(max)cTxs.t.Ax=bx≥0 其中 x x x为n维列向量, c T c^{T} cT为n维行向量,A
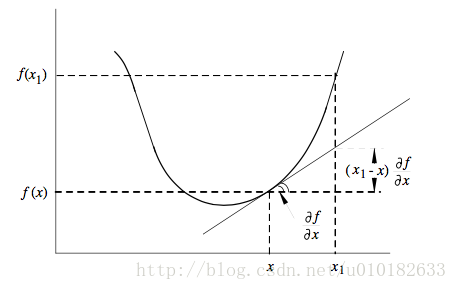
漫步最优化十四——凸函数与凹函数
我一直都在流浪, \textbf{我一直都在流浪,} 可我却不曾见过海洋。 \textbf{可我却不曾见过海洋。} 我努力微笑坚强, \textbf{ 我努力微笑坚强,} 用寂寞筑成一道围墙。 \textbf{用寂寞筑成一道围墙。} 如果恨你,就没发忘记你, \textbf{如果恨你,就没发忘记你,} 如果不够悲伤,就无法飞翔。 \textbf{如果不够
漫步最优化十一——局部极小与极大的充分必要条件(上)
即便没有那么多浪漫的话, \textbf{即便没有那么多浪漫的话,} 我也想与你走过每个冬夏。 \textbf{我也想与你走过每个冬夏。} 你的出现是我唯一的心动, \textbf{你的出现是我唯一的心动,} 你的与众不同让我难以忘记每个笑容。 \textbf{你的与众不同让我难以忘记每个笑容。} 越相处越习惯你, \textbf{越相处越习惯你,} 越想
漫步最优化五——可行域
我不介意你慢慢的到来, \textbf{我不介意你慢慢的到来,} 我也不介意我们多少次擦肩而过, \textbf{我也不介意我们多少次擦肩而过,} 因为我一直相信我们都在相遇的路上马不停蹄。 \textbf{因为我一直相信我们都在相遇的路上马不停蹄。} ——畅宝宝的傻逼哥哥 \qquad\qquad\qquad\qquad\quad\textbf{——畅宝宝的傻逼哥哥
漫步最优化四——约束
你从天而降的那刻起,我的世界变得难以言喻。 \textbf{你从天而降的那刻起,我的世界变得难以言喻。} 从陌生到熟悉,我从来没有奢望过爱情的到来。 \textbf{从陌生到熟悉,我从来没有奢望过爱情的到来。} 但是我却忙于快乐,忙于感动,忙于牵挂。 \textbf{但是我却忙于快乐,忙于感动,忙于牵挂。} 这一刻,我想勇敢地说:宝宝,我爱你。 \textbf{这一刻
机器学习为什么要学习最优化呢?
最优化方法(也称做运筹学方法)是近几十年形成的,它主要运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。最优化方法的主要研究对象是各种有组织系统的管理问题及其生产经营活动。最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。实践表明,随着科学技术的日益进步和生产经营的日益发展,最优化方法已成为现代
机器学习中的最优化算法有哪些?
我们日常生活中遇到过很多最优化问题,比如如何在最短时间内从A点到达B点?如何投入最少工作量却获得最大的效益?如何设计发动机使得油耗最少而功率最大?可见,最优化的作用十分强大。接下来,我们介绍几个最优化算法,并利用它们训练出一个非线性函数用于分类。 1、Logistic回归 **优点:**计算代价不高,易于理解和实现。 缺点:容易欠拟合,分类精度可能不高。 适用数据类型:数值型和标称型数据。
机器学习——最优化模型
最优化模型的概述: 从某种程度上说,我们的世界是由最优化问题组成的。每一天,我们的生活都面临无数的最优化问题:上班怎么选择乘车路线,才能舒服又快速地到达公司;旅游如何选择航班和宾馆,既省钱又能玩地开心;跳槽应该选择哪家公司,钱多、事少、离家近;买房子应该选在哪里,交通发达有学区,生活便利升值快。 可以看出,上面所有的问题都面临无数的选择,我们会根据自己的偏好对每个选择打一个不同的分数,再从所有
支持向量机(三)序列最小最优化算法(SMO)
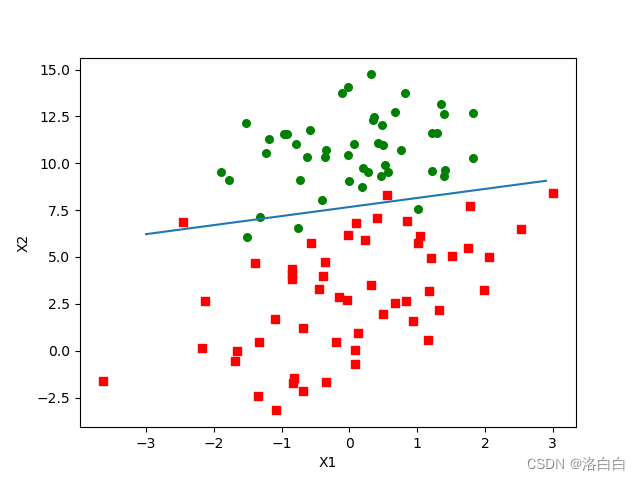
在支持向量机(一)和支持向量机(二)两篇文章中,我们分别介绍了线性可分的支持向量机和线性向量机,从中可知,我们最终的目的是要计算得出支持向量对应的拉格朗日乘子α,但是我们并没有说怎么算。这篇文章主要介绍了序列化最小优化算法,用来计算α。在介绍之前我们先简单介绍一下其中用到的核函数。 核函数 首先我们看下面的两个图:
最优化问题简介及优秀教材《凸优化》介绍
前言 最优化广泛应用于科学与工程计算、数据科学、机器学习、人工智能、图像和信号处理、金融和经济、管理科学等众多领域。 最优化问题可以归纳为如下定义: 最优化问题一般很难求解,除了一些特例。目前已经发展成熟的,能够有效求解的最优化问题可以归为以下三类: 最小二乘问题 least-squares problems线性规划问题 linear programming problems凸优化问题 con
优化投资组合:DolphinDB 最优化求解系列函数应用指南
线性规划和非线性规划是运筹学中重要的内容,在金融和经济领域的问题解决中具有广泛的应用。在金融量化领域的多因子量化模型中,组合权重优化起着至关重要的作用,组合权重优化包括两个要素:第一是组合权重优化的目标函数,如最大化期望收益率,最小化组合风险,最大化效用函数等,第二是目标函数相对应的约束条件,如等式约束和不等式约束。这些优化内容都是线性规划和非线性规划的重要应用问题。 在多因子量化投资领域中,不
进化策略入门:最优化问题的另一种视角
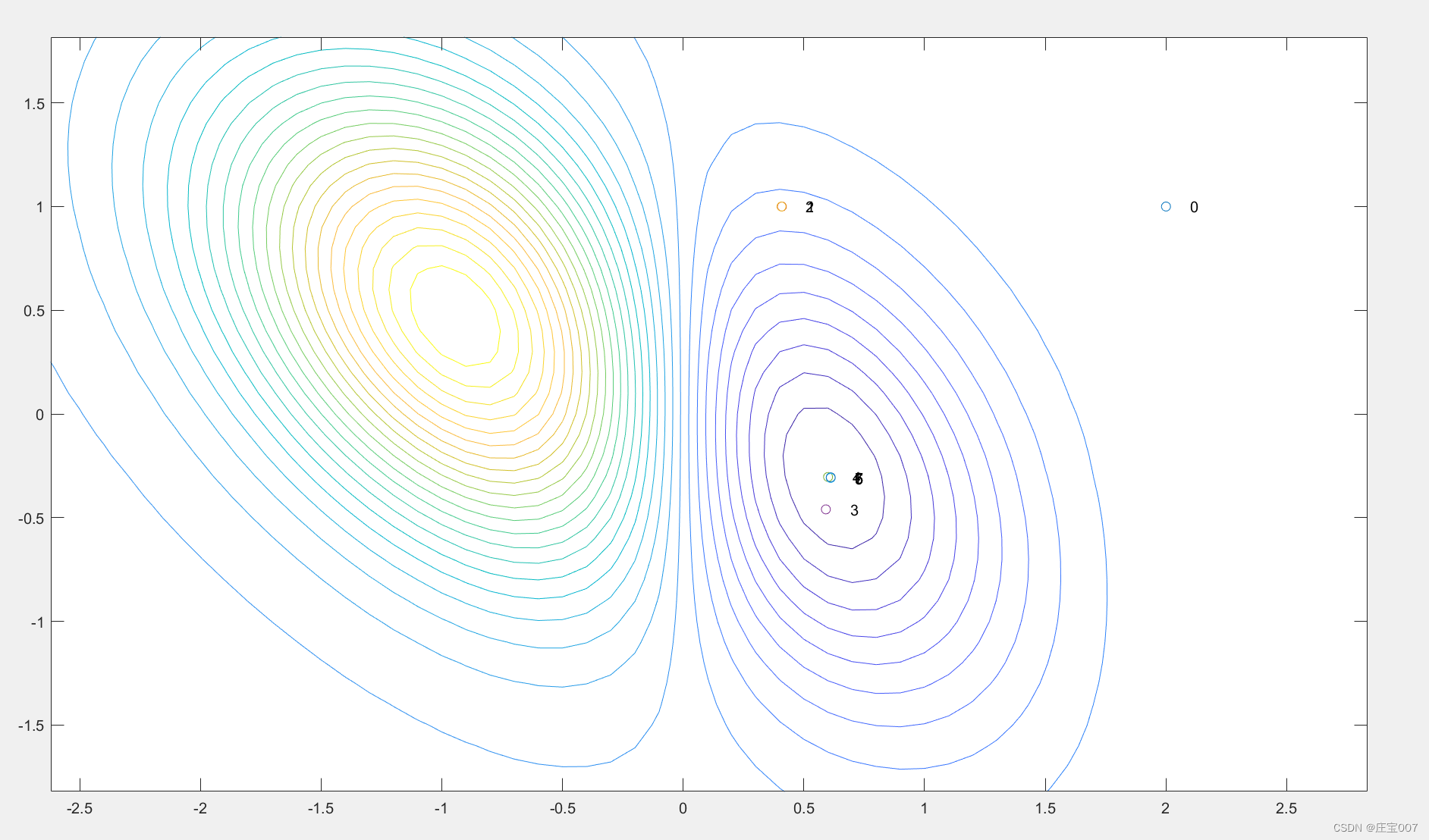
otoro.net的系列技术博客之一 本文将通过一些可视化的案例向大家解释进化策略是如何工作的。为了方便更多入门读者理解本文,我将对相关公式做简化处理。同时,我也为希望理解更多数学细节的读者提供了相关数学公式的原始论文。这是本系列的第一篇文章,在本系列中,我会向大家介绍如何在诸如 MNIST、OpenAI Gym、Roboschool、PyBullet 等任务中应用这些算法。 引言 神经网络
【scipy】scipy.optimize 求解非线性Rosenbrock最优化问题 python
利用python软件编程求解非线性Rosenbrock最优化问题 m i n f ( x , y ) = ( 1 − x ) 2 + 100 ( y − x 2 ) 2 min f(x, y) = (1-x)^{2}+100(y-x^{2})^{2} minf(x,y)=(1−x)2+100(y−x2)2 − 2 ≤ x ≤ 2 -2\leq x \leq 2 −2≤x≤2 − 1 ≤
大连理工大学 2021年最优化方法大作业(2)
接上一篇文章,这次分享一下其他的三种算法,上一篇编写的不精确一维线搜索需要用到,链接在这:大连理工大学 2021年最优化方法大作业(1)_JiangTesla的博客-CSDN博客 下一道题在这:大连理工大学2021最优化方法大作业(3)_JiangTesla的博客-CSDN博客 2022题目的小补充大连理工大学2022上半年最优化方法大作业_Jiang_Tesla的博客-CSDN博客
![[最优化方法] 《最优化方法》个人问答式学习笔记 with LLM](https://i-blog.csdnimg.cn/direct/6d0179d218ce4971a16401b0d872f04b.png)