本文主要是介绍支持向量机（三）序列最小最优化算法（SMO），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
在支持向量机（一）和支持向量机（二）两篇文章中，我们分别介绍了线性可分的支持向量机和线性向量机，从中可知，我们最终的目的是要计算得出支持向量对应的拉格朗日乘子α，但是我们并没有说怎么算。这篇文章主要介绍了序列化最小优化算法，用来计算α。在介绍之前我们先简单介绍一下其中用到的核函数。
- 核函数
首先我们看下面的两个图：
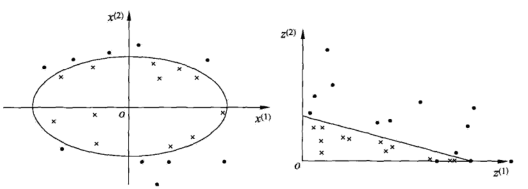
我们看上面的两个图，右边的明显是可以用一个直线将数据分开，那就是线性可分的，而左边的图是用一个曲线将数据分开的，这个问题就称之为非线性可分的问题。而非线性问题往往不好求解，而我们希望的就是能用线性求解的问题来求解非线性的问题，方法就是进行一个变换，将非线性问题变成线性问题。
再看上面左图，是个椭圆的形式，给出椭圆的函数
，这个函数明显是非线性函数，下面我们将其做变换令:
然后我们将其原式替换，得到：
可以看到经过简单的变换，将原来的非线性问题转化为了式1的线性问题。这就是核技巧的基本思想。
核技巧分为两步：首先使用一个变换将原空间的数据映射到新空间；然后在新空间里用线性分类学习方法从训练数据中学习分类模型。
进行数据映射的话，我们就用到了核函数：
其中K(x,z)就是核函数，φ(x)成为映射函数，就是将原空间映射到新空间的映射方式，对应上面的例子φ(x)=x2，φ(x)∙φ(z)就是两个映射的內积。
下面我们再看先线性支持向量机的目标函数：
我们将式2中的xi和xj的內积替换成映射的內积，即映射后的求解最优值问题：
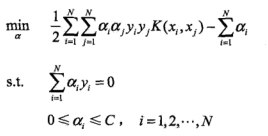
然后求解最优解
线性支持向量机的最终分类函数形式如下：
同样将xi和x的內积形式替换为K(xi,x)得：
我们常用的核函数有：
&#
这篇关于支持向量机（三）序列最小最优化算法（SMO）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
