本文主要是介绍凸数据集与凸函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
凸数据集与凸函数
- 凸数据集
- 凸函数
- 定义
- 判定方法
凸数据集
如果一个数据集D是凸的,那么对于其中任意的两点x,y∈D,θ∈R,0≤θ≤1,
则 θ x + ( 1 − θ ) y ∈ D
表达式θx+(1−θ)y被称作点x , y 的凸性组合(convex combination)
通俗的讲,就是数据集D中任意两点的连线上的点,也在数据集D内,那么数据集D就是一个凸集。
如下图,左边非凸,右边为凸
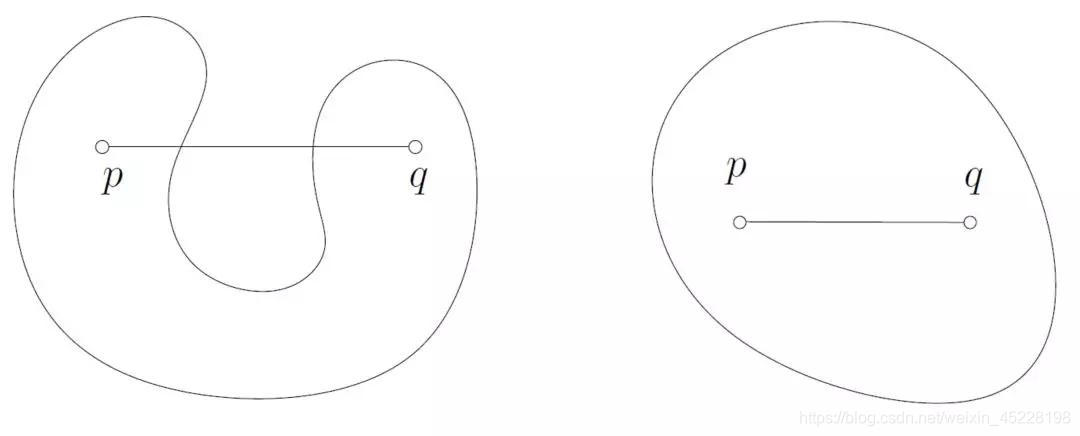
常见的凸数据集:
1. R n R^n Rn,n维实数空间,由定义可知
2.凸集的交集
3.n维半正定矩阵的集合
等
参考链接:https://blog.csdn.net/qq_19528953/article/details/88600926
凸函数
定义
一个函数f : R n R^n Rn → R,如果它的域D(f)是一个凸集,

那么函数f 就是一个凸函数
几何上,任意两点的连线在这两点函数部分的上面。
判定方法
-
一阶充分必要条件(不好用)
对于凸集D(f), 任意两点x,y ∈ D, 有
f ( y ) f(y) f(y)≥ f ( x ) f(x) f(x)+ ∇ x ∇_x ∇x f ( x ) T f(x)^T f(x)T ( y − x ) (y−x) (y−x) -
二阶充分必要条件
∇ x 2 ∇^2_x ∇x2 f ( x ) f(x) f(x)≥0 -
举例子
i. 指数函数 是凸函数,如 f(x)= e a x e^{ax} eax , a∈R
其二阶导数 f ′ ′ ( x ) f ^{′ ′ }( x ) f′′(x) = a 2 a^2 a2 $e^{a x} $
这篇关于凸数据集与凸函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




