pcl中的PFH和FPFH

本文主要是介绍pcl中的PFH和FPFH，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

PFH

点特征直方图计算方式

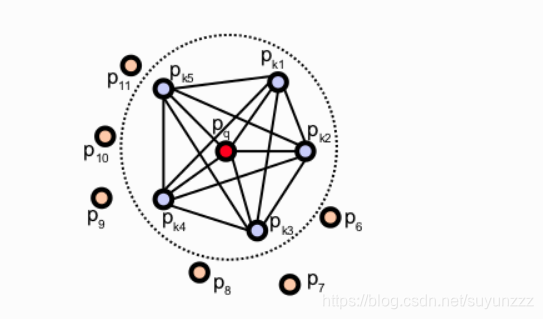
注意
这里图上标注的角度并不是真实的角度，而是对应角度的余弦值(按理说是内积，但是模长都是1)，可以从这个代码中的pcl::computePairFeatures函数看出:

bool
pcl::computePairFeatures (const Eigen::Vector4f &p1, const Eigen::Vector4f &n1, const Eigen::Vector4f &p2, const Eigen::Vector4f &n2,float &f1, float &f2, float &f3, float &f4)
{Eigen::Vector4f dp2p1 = p2 - p1;dp2p1[3] = 0.0f;f4 = dp2p1.norm ();if (f4 == 0.0f){PCL_DEBUG ("[pcl::computePairFeatures] Euclidean distance between points is 0!\n");f1 = f2 = f3 = f4 = 0.0f;return (false);}Eigen::Vector4f n1_copy = n1,n2_copy = n2;n1_copy[3] = n2_copy[3] = 0.0f;float angle1 = n1_copy.dot (dp2p1) / f4;// Make sure the same point is selected as 1 and 2 for each pairfloat angle2 = n2_copy.dot (dp2p1) / f4;if (std::acos (std::fabs (angle1)) > std::acos (std::fabs (angle2))){// switch p1 and p2n1_copy = n2;n2_copy = n1;n1_copy[3] = n2_copy[3] = 0.0f;dp2p1 *= (-1);f3 = -angle2;}elsef3 = angle1;// Create a Darboux frame coordinate system u-v-w// u = n1; v = (p_idx - q_idx) x u / || (p_idx - q_idx) x u ||; w = u x vEigen::Vector4f v = dp2p1.cross3 (n1_copy);v[3] = 0.0f;float v_norm = v.norm ();if (v_norm == 0.0f){PCL_DEBUG ("[pcl::computePairFeatures] Norm of Delta x U is 0!\n");f1 = f2 = f3 = f4 = 0.0f;return (false);}// Normalize vv /= v_norm;Eigen::Vector4f w = n1_copy.cross3 (v);// Do not have to normalize w - it is a unit vector by constructionv[3] = 0.0f;f2 = v.dot (n2_copy);w[3] = 0.0f;// Compute f1 = arctan (w * n2, u * n2) i.e. angle of n2 in the x=u, y=w coordinate systemf1 = std::atan2 (w.dot (n2_copy), n1_copy.dot (n2_copy)); // @todo optimize thisreturn (true);
}

vector组合方式

pcl中对其实现使用了三个角度,而没有使用长度,对每一个角度划分为5个区域(bin),然后接下来就是将这3种特征的5个Bin组合成一个vector,有两张方式:

1. 将这个5*3个bin直接组合在一块,特征只有15个值,最终的直方图横轴就只有15个坐标.FPFH就是采用的这种方式
2. 讲这3种特征按照各自的阈值分为5类,一共分为15类.比如第一对点的特征为:3,4,4,然后根据5进制转10进制的方式,将其转为10进制数:3x1+4x5+4x25=123.因此,这种方式会有125个横坐标值.FPH就是采用的这种方式

第二种的计算方式如下:
pcl中采用3个角度特征,bin设为5,采用10进制计数,最终为555=125

The default PFH implementation uses 5 binning subdivisions (e.g., each of the four feature values will use this many bins from its value interval), and does not include the distances (as explained above – although the computePairFeatures method can be called by the user to obtain the distances too, if desired) which results in a 125-byte array (5^3) of float values. These are stored in a pcl::PFHSignature125 point type.

FPFH

FAST点特征直方图计算方式

pcl中对FPFH的实现依旧使用了3个角度,但是对bin的划分提升到了11个区域,feature vector的组合方式采用了直接拼接的方式所以为33

The default FPFH implementation uses 11 binning subdivisions (e.g., each of the four feature values will use this many bins from its value interval), and a decorrelated scheme (see above: the feature histograms are computed separately and concantenated) which results in a 33-byte array of float values. These are stored in a pcl::FPFHSignature33 point type.

参考

PFH
FPFH

这篇关于pcl中的PFH和FPFH的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---