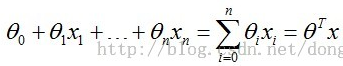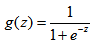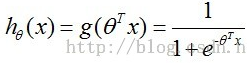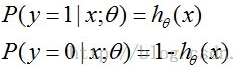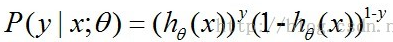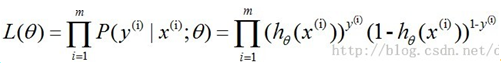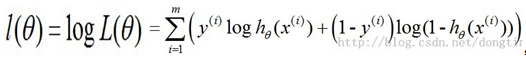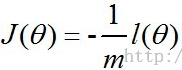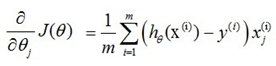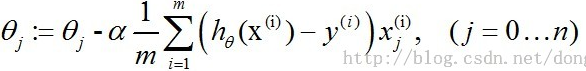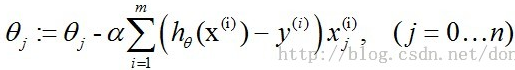本文主要是介绍Logistic Regression(逻辑斯特回归),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Logistic Regression实际上是基于Linear Regression的,与Linear Regression的不同在于输出增加了一个非线性映射,即应用逻辑斯特函数将回归结果映射到0到1(能够将负无穷到正无穷映射到0-1的函数有很多,但是Logistic函数求导结果很简洁,能让伯努利的指数分布式标准形式(待理解)),从而可以利用概率来分类。
下面讲一下LR 的推导过程。我们按照解决机器学习算法一般过程来推导。即:
1. 建立模型---h(x)
2. 写出代价函数(CostFunction)---由最大似然估计推导得出
3. 求解代价函数取最小值时的参数值---梯度下降。
具体过程:
1.首先是建立模型
现在我们假设在二维平面上有两类数据要进行分类。假定数据是线性可分的,我们可以用一条直线来将他们分开。
直线的方程为:
,其实这就是多元线性回归方程。
而Logistic函数为:
我们把多元线性回归方程的输出作为自变量代入逻辑斯特函数,进而构造预测模型为:
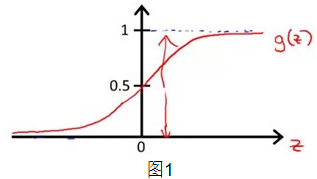
我们最终要得到的就是这个模型h(x)。将待新样本点输入h(x)求出的值即为该样本为正例的概率。反之1-h(x)即为该样本为负例的概率((我们可以看下面图1,当z(即)趋近于正无穷时(正例),h(x)=g(z)趋近于1,即为正例的概率为1,为负例的概率为1-h(x)趋近于0),反之当z趋近于负无穷(负例)时,为正例的概率h(x)趋近于0,为负例的概率1-h(x)趋近于1。
2.然后具体推导损失函数
损失函数的推导应用了最大似然估计,最大似然估计就是最终我们要求解的参数值应该是让现有训练样本观测值的概率最大,前面我们得出结论
,把这个式子综合起来就是
,取似然函数
,为了方便计算,取对数似然函数得到
,最大似然估计就是要求使得l(θ)最大的θ,为了能方便的应用梯度下降法求解参数我们在这里取损失函数为:
,求对数似然函数的最大就是求J(θ)的最小,下面讲一下用梯度下降法求解最优参数过程。
3.梯度下降求解参数
首先是J(θ)对求导。
然后在J(θ)负梯度方向上更新的值,即
,其中@为学习速率。这里由于的存在可以省略1/m。即
最终会收敛,分类模型因此求出。
这篇关于Logistic Regression(逻辑斯特回归)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!