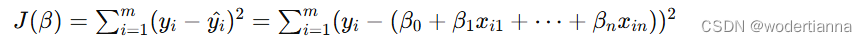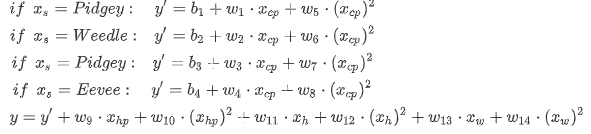regression专题

perl的学习记录——仿真regression

1 记录的背景之前只知道有这个强大语言的存在，但一直侥幸自己应该不会用到它，所以一直没有开始学习。然而人生这么长，怎就确定自己不会用到呢？这次要搭建一个可以自动跑完所有case并且打印每个case的pass信息到指定的文件中。从而减轻手动跑仿真，手动查看log信息的重复无效低质量的操作。下面简单记录下自己的思路并贴出自己的代码，方便自己以后使用和修正。 2 思路整理作为一个IC d

Spark MLlib模型训练—回归算法 Linear regression

Spark MLlib模型训练—回归算法 Linear regression 线性回归是回归分析中最基础且应用广泛的一种方法。它用于建模目标变量和一个或多个自变量之间的关系。随着大数据时代的到来，使用像 Spark 这样的分布式计算框架进行大规模数据处理和建模变得尤为重要。本文将全面解析 Spark 中的线性回归算法，介绍其原理、参数、Scala 实现、代码解读、结果分析以及实际应用场景。 1

Spark MLlib模型训练—回归算法 GLR( Generalized Linear Regression)

Spark MLlib模型训练—回归算法 GLR( Generalized Linear Regression) 在大数据分析中，线性回归虽然常用，但在许多实际场景中，目标变量和特征之间的关系并非线性，这时广义线性回归（Generalized Linear Regression, GLR）便应运而生。GLR 是线性回归的扩展，能够处理非正态分布的目标变量，广泛用于分类、回归以及其他统计建模任务。

regression and anova

regression一般是统计学的回归回归,研究一个随机变量Y对另一个(X)或一组(X1,X2,…,Xk)变量的相依关系的统计分析方法.研究一个或多个随机变量Y1 ,Y2 ,…,Yi与另一些变量X1、X2,…,Xk之间的关系的统计方法.又称多重回归分析.通常称Y1,Y2,…,Yi为因变量,X1、X2,…,Xk为自变量.回归分析是一类数学模型,特别当因变量和自变量为线性关系时,它是一种特殊

机器学习—线性回归算法（Linear Regression）

目录一、基本概念二、线性回归简单分类与模型三、线性回归的关键步骤四、线性回归问题分析五、线性回归问题的解法1、最小二乘法2、梯度下降法六、线性回归中的过拟合与欠拟合1、过拟合1、岭回归（Ridge Regression）2、套索回归 (Lasso回归)（Lasso Regression）3、弹性网（Elastic Net） 2、欠拟合七、线性回归中的超参数与模型评估方法1、超参数（Hy

logstic regression

李宏毅的ppt：http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/Logistic%20Regression%20(v3).pdf

Logistic Regression本质上还是Linear Regression的一种，只是用了一个Logistic Function将线性回归的连续值映射到了 { 0 , 1 } \{0, 1\} {0,1}空间。因此Linear Regression只能对具有线性边界的分类问题有很好的预测效果，对于非线性的边界是无能为力的。至于下面这张很经典的大家常用的图，只是做了一个feature map

Linear Regression学习笔记

回归主要分为线性回归和逻辑回归。线性回归主要解决连续值预测问题，逻辑回归主要解决分类问题。但逻辑回归输出的是属于某一类的概率，因此常被用来进行排序。 1. 线性回归的原理假定输入 χ \chi和输出 y y之间有线性相关关系，线性回归就是学习一个映射 f:χ→yf: \chi \to y 然后对于给定的样本 x x，预测其输出： y^=f(x)\hat y=f(x) 现假定 x=

线性回归（Linear Regression）原理详解及Python代码示例

一、线性回归原理详解线性回归是一种基本的统计方法，用于预测因变量（目标变量）与一个或多个自变量（特征变量）之间的线性关系。线性回归模型通过拟合一条直线（在多变量情况下是一条超平面）来最小化预测值与真实值之间的误差。 1. 线性回归模型对于单变量线性回归，模型的表达式为：其中： y是目标变量。x是特征变量。β0是截距项（偏置）。β1

ython机器学习分类算法（六）-- 逻辑回归（Logistic Regression）

逻辑回归原理逻辑回归虽然名为“回归”，但实际上是一种用于处理二分类或多分类问题的分类算法。其核心思想是，利用线性回归模型的预测结果逼近真实标记的对数几率（log odds），因此得名“逻辑回归”。具体来说，逻辑回归通过引入sigmoid函数（或称为逻辑函数），将线性回归模型的输出值映射到0和1之间，从而可以将其解释为某个类别发生的概率。对于二分类问题，假设输

机器学习 - 线性回归(Linear Regression)

1. 目标线性回归是希望通过对样本集进行有监督的学习之后，找出特征属性与标签属性之间的线性关系 Θ \Theta Θ。从而在获取没有标签值的新数据时，根据特征值和线性关系，对标签值进行预测。 2. 算法原理 2.1 线性模型（Linear Model）在二维平面坐标系中，一条直线可表示为： f ( x ) = θ 1 x + θ 0 f(x) = \theta_1x + \thet

如何通俗理解逻辑回归(Logistic Regression)

首先, 什么是逻辑回归呢? 我们先来看一下逻辑回归的公式: t = w T X + b y = s i g m o i d ( t ) s i g m o i d ( t ) = 1 1 + e − t t = w^TX+b\\ y = sigmoid(t)\\ sigmoid(t) = \frac1{1+e^{-t}} t=wTX+by=sigmoid(t)sigmoid(t)=1+e−t1

ICCV2017《Deep Direct Regression for Multi-Oriented Scene Text Detection》阅读笔记

前言本文是对《Deep Direct Regression for Multi-Oriented Scene Text Detection》论文的简要介绍和细节分析，由于作者没有放出源码，所以本文没有源码解读的部分，有关的复现工作将在下篇博客介绍。注：编者水平有限，如有谬误，欢迎指正。若要转载，请注明出处，谢谢。联系方式：邮箱：yue_zhan@yahoo.com QQ：11563566

史上最直白的logistic regression教程之二

实现线性拟合我们用python2.7实现上一篇的推导结果。请先安装python matplotlib包和numpy包。具体代码如下: #!/usr/bin/env python #! -*- coding:utf-8 -*-import matplotlib.pyplot as pltfrom numpy import *#创建数据集def load_dataset():n = 1

【逻辑回归】Logistic Regression逻辑回归模型学习笔记

文章目录序言1. 线性回归2. 逻辑回归2.1 引入逻辑回归的原因2.2 逻辑回归2.3 逻辑回归的应用 3. 逻辑函数3.1 sigmoid函数3.2 sigmoid函数的性质3.3 决策边界3.4 对数几率 4. 损失函数4.1 为什么说逻辑回归时概率类模型4.2 为什么要进行极大似然估计4.3 利用MLE如何推导出损失函数4.4 损失函数/代价函数/目标函数 5. 最优化问题6. s

使用logistic regression 处理良/恶性肿瘤分类任务案例

1.读入数据 2.随机切分数据集，把数据集切分成训练集和测试集 3.对数据集进行标准化 4.创建logistic regression 模型，在训练集上训练数据 5.在测试集上进行预测分类 logistic regression 预测的准确率：0.9883040935672515 # -*- coding:utf-8 -*-import pandas as pdimport num

【机器学习】三、逻辑回归(Logistic Regression)

目录背景逻辑回归算法目标算法推演逻辑函数（Logstic Function) 假设函数代价函数（Cost Function) 梯度下降函数算法实现案例案例分析及代码实现读取数据特征选择参数theta定义代价函数梯度下降最小化拟合主函数结果验证图形化展示背景本文内容所使用的python包及别名：（pytho

[Kaggle]House Prices: Advanced Regression Techniques

1、背景说明 2、前期准备 3、程序设计 4、知识点说明 5、测试结果 6、总结 7、附录：解释特征 1、背景说明 1.1 项目名称： House Prices_Advanced Regression Techniques https://www.kaggle.com/c/house-prices-advanced-regression-techniques 1.2 实现目

机器学习之快速森林分位数回归（Fast Forest Quantile Regression）

快速森林分位数回归（Fast Forest Quantile Regression）是一种用于回归任务的机器学习方法，旨在预测目标变量的特定分位数值。与传统回归模型不同，分位数回归能够提供目标变量的不同分布信息，而不仅仅是均值预测。这在需要估计不确定性范围或分布特征的应用中非常有用。 1. 核心概念回归树：用于回归任务的决策树，通过一系列分裂条件预测连续目标变量。随机森林：通过集成多棵回归树

最小角回归(least angle regression) 的一点记录

least angle regression (LARS) 给定线性无关按行排列的数据 X=(x1,...,xn)T X=(x_1,...,x_n)^T，数据label y y。不妨假设XX中心化且列归一化， y y去中心化,即∑i=1nyi=0,∑i=1nxij=0,∑i=1nx2ij=1\sum_{i = 1}^n y_i = 0,\quad \sum_{i=1}^n x_{ij}=0,

Backtracking Regression Forests for Accurate Camera Relocalization

这种方法其实类似 deep learning，只不过是以森林的方式进行train，森林是由一系列的决策树组成。每个决策树中的每个节点都是待训练的参数：决策树的目的是：，即输入是image，depth（如果有的话），2d pixel位置，输出是3d点的位置x y z + 最终的feature。因此决策树可以认为是一个从2d到3d的映射，这样的话就导致每个场景就需要

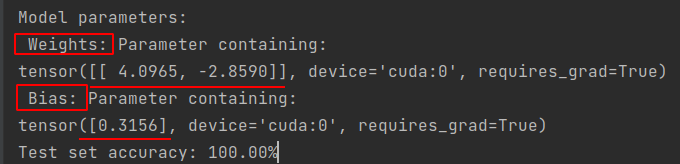
Pytorch 入门之-- 逻辑回归 Logistic_Regression

代码+注释 __author__ = 'SherlockLiao'import torchfrom torch import nn, optimimport torch.nn.functional as Ffrom torch.autograd import Variablefrom torch.utils.data import DataLoaderfrom torchvision

Andrew Ng机器学习week6(Regularized Linear Regression and Bias/Variance)编程习题

Andrew Ng机器学习week6(Regularized Linear Regression and Bias/Variance)编程习题 linearRegCostFunction.m function [J, grad] = linearRegCostFunction(X, y, theta, lambda)%LINEARREGCOSTFUNCTION Compute cost an

一个例子搞懂softmax regression

softmax regression简介 logistic regression (LR) 常用于二分类问题。对于多分类问题，使用softmax regression (SMR) 则是一个更好的选择，SMR也是逻辑回归在多分类问题上的一个推广。下图分别显示了LR和SMR的训练过程和差别所在：为了适应多分类问题，SMR使用softmax函数（ Φ \Phi Φ）代替了原来的sigmoid

polynomial regression

在上一节所介绍的非线性回归分析，首先要求我们对回归方程的函数模型做出判断。虽然在一些特定的情况下我们可以比较容易地做到这一点,但是在许多实际问题上常常会令我们不知所措。根据高等数学知识我们知道，任何曲线可以近似地用多项式表示，所以在这种情况下我们可以用多项式进行逼近，即多项式回归分析。一、多项式回归方法假设变量y与x的关系为p次多项式，且在xi处对y的随机误差 (i=1,2,…,

机器学习 | Regression

机器学习的步骤对现有问题，找出一个数学模型，例如 y = w*x +b （其中，w&b值待定，因此组成了一个function set)。定义一个评价函数，用训练数据去评估function set中的function效果。找出一个最好的函数，确定模型参数（如何从若干参数值中找出合适的模型参数：梯度下降法）用训练数据测试数学模型，用评价函数评估如果训练结果不好，改进数学模型，迭代设计。梯度下