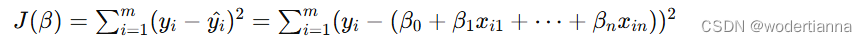本文主要是介绍regression and anova,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
regression一般是统计学的回归回归,研究一个随机变量Y对另一个(X)或一组(X1,X2,…,Xk)变量的相依关系的统计分析方法.研究一 个或多个随机变量Y1 ,Y2 ,…,Yi与另一些变量X1、X2,…,Xk之间的关系的统计方法.又称多重回归分析.通常称Y1,Y2,…,Yi为因变量,X1、X2,…,Xk为自变量.回归分析是一类数学模型,特别当因变量和自变量为线性关系时,它是一种特殊的线性模型.最简单的情形是一个自变量和一个因变量,且它们大体上有线性关系,这叫一元线性回归,即模型为Y=a+bX+ε,这里X是自变量,Y是因变量,ε是随机误差,通常假定随机误差的均值为0,方差为σ^2(σ^2大于0)σ^2与X的值无关.若进一步假定随机误差遵从正态分布,就叫做正态线性模型.一般的情形,若有k个自变量和一个因变量,因变量的值可以分解为两部分:一部分是由自变量的影响,即表示为自变量的函数,其中函数形式已知,但含一些未知参数;另一部分是由于其他未被考虑的因素和随机性的影响,即随机误差.当函数形式为未知参数的线性函数时,称线性回归分析模型;当函数形式为未知参数的非线性函数时,称为非线性回归分析模型.当自变量的个数大于1时称为多元回归,当因变量个数大于1时称为多重回归.
anova是方差分析
方差是各个数据与平均数之差的平方的平均数.在概率论和数理统计中,方差(英文Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度.在许多实际问题中,研究随机变量和均值之间的偏离程度有着很重要的意义.
方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”或“F检验”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验.由于各种因素的影响,研究所得的数据呈现波动状.造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素.
这篇关于regression and anova的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!