本文主要是介绍【机器学习(5)】Scikit-learn创建线性回归模型(LinearRegression、Lasso及Ridge)和逻辑回归模型(logistic),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 数据加载
假如进行房价的预测,这里加载的数据共1000条,共十个维度(十个特征),除了id以外,其余的都是自变量(9个可用)
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
os.chdir(r"C:\Users\86177\Desktop")df = pd.read_csv('sample_data_sets.csv')
print(df.columns)
print(df.shape)
–> 输出的结果为:
Index(['id', 'complete_year', 'average_price', 'area', 'daypop', 'nightpop','night20-39', 'sub_kde', 'bus_kde', 'kind_kde'],dtype='object')(1000, 10)
自变量参数讲解:complete_year房子建造年代、average_price平均价格、area房间面积、daypop白天人口密度、nightpop夜间人口密度、night20-3920-39岁夜间人口密度、sub_kde地铁服务水平、bus_kde公交车服务水平、kind_kde幼儿园服务水平
2. 提取自变量和制作因变量标签
1) 通过上述列举的9个自变量参数,可以发现前两个对于其他参数来说重要性程度偏低,可以选择后面7个参数作为自变量
2) 因变量标签这里,采用平均价格的中位数进行标定,如果超过这个中位数,就定位高房价,低于这个中位数,就是低房价
代码实现如下:(为了保护数据的完整性和防止数据被破坏,这里先制作标签,然后再将数据进行复制,最后操作的是数据副本)
price_median = df['average_price'].median()
print(price_median)
df['is_high'] = df['average_price'].map(lambda x: True if x>= price_median else False)
print(df['is_high'].value_counts())
–> 输出的结果为:(先取平均价格的中位数,再创建一个因变量标签)
30519.0
True 500
False 500
Name: is_high, dtype: int64
数据复制并提取自变量和因变量(注意,线性回归使用的都是y_train数值型标签,后面的逻辑回归使用的是y_label类别型标签)
# 提取自变量:数值型
x_train = df.copy()[['area', 'daypop', 'nightpop', 'night20-39', 'sub_kde', 'bus_kde', 'kind_kde']]
# 提取因变量:数值型
y_train = df.copy()['average_price']
# 提取因变量:类别型
y_label = df.copy()['is_high']
3. 创建Pipeline对象和构建线性模型
为了熟悉并掌握创建模型的工作流(数据预处理,标准化,纠偏等过程),这里将整个流程封装在Pipeline的对象中,该对象中需要引入一个list列表,也就是所有步骤的汇总所在地,基本步骤包含两个要素: 步骤的命名 和 模型对象(里面是有参数的)
3.1 加载模块、构造模型并拟合
这里传入的参数是fit_intercept=True,要求模型去拟合截距值,也就是b值,如果是False,返回的结果也就没有b值,(因为只有一个线性模型,Pipeline里面就只有一个数据)
# 加载pipeline
from sklearn.pipeline import Pipeline
# 加载线性回归模型
from sklearn.linear_model import LinearRegression
# 构建线性回归模型
pipe_lm = Pipeline([('lm_regr',LinearRegression(fit_intercept=True))])
# 训练线性回归模型
pipe_lm.fit(x_train, y_train)
# 使用线性回归模型进行预测
y_train_predict = pipe_lm.predict(x_train)
3.2 查看线性模型特征参数和截距值
.coef_ / .intercept_ 分别代表特征参数(coefficient)和截距值(intercept)
# 查看线性回归模型特征参数
print(pipe_lm.named_steps['lm_regr'].coef_)
# 查看线性回归模型截距值
print(pipe_lm.named_steps['lm_regr'].intercept_)
–> 输出的结果为:(输出的是7个参数一个b值)
[ 9.68026492e+00 3.45789754e+00 -1.68662269e+01 4.34410864e+015.92819921e+04 3.41972844e+03 9.69441685e+03]24662.078913322737
3.3 提取模型特征参数及对应的名称
提取完相应的数据之后,将其创建为DataFrame数据
# 提取模型特征参数
coef = pipe_lm.named_steps['lm_regr'].coef_
# 提取对应的特征名称
features = x_train.columns.tolist()
# 构建参数df
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)
–> 输出的结果为:(这里的特征名称,其实就是当初索引的几个列标题)
feature coefficient
0 area 9.971842
1 daypop 3.720621
2 nightpop -17.122363
3 night20-39 43.528716
4 sub_kde 59019.531359
5 bus_kde 3309.771544
6 kind_kde 9410.012382
3.4 绘制参数柱状图
matplotlib库前面已经导入过了,这里可以直接使用,这一步主要是看一下7个参数的影响水平如何
# 绘制参数特征值柱状图
coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()
–> 输出的结果为:
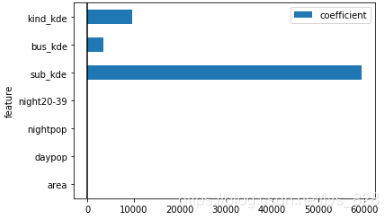
由上图可知,最后三个(在最上面的数据是排在最后的)服务水平的特征值远远大于前四个参数的,要查看前四个的相关数据,可以单独绘制图像,如下
# 绘制参数特征值柱状图
coef_table.set_index(['feature']).iloc[0:4].plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()
–> 输出的结果为:
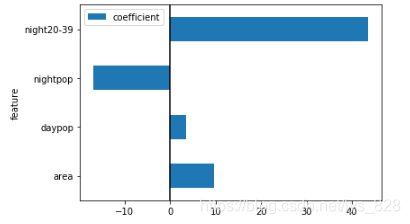
4 构建Lasso回归模型
前面讲了有关Pipeline对象的知识,直接就可以直接加载框架了,构建Lasso回归模型
4.1 加载模块、构造模型并拟合
这一步几乎和上面创建线性模型类似,不同的就是在于Pipeline对象列表中的内容发生了变化,参数添加了一个alpha,其大小就是控制L1正则系数的影响力,其值越大,L1正则系数对模型的约束也就越大(回顾上一篇的讲解)
# 加载lasso回归模型
from sklearn.linear_model import Lasso
# 构建线性回归模型
pipe_lasso = Pipeline([('lasso_regr',Lasso(alpha=500, fit_intercept=True))])
# 训练线性回归模型
pipe_lasso.fit(x_train, y_train)
# 使用线性回归模型进行预测
y_train_predict = pipe_lasso.predict(x_train)
4.2 查看线性模型特征参数和截距值
# 查看线性回归模型特征参数
print(pipe_lasso.named_steps['lasso_regr'].coef_)
# 查看线性回归模型截距值
print(pipe_lasso.named_steps['lasso_regr'].intercept_)
–> 输出的结果为:(可以看出其中的几个参数已经为0了,)
[ 27.03261599 6.97427277 -14.89931364 33.19206407 0.0. 0. ]
26065.635086213653
上述的结果也就对应了上篇文章中提到的有关L1正则系数相关的知识点,如下

4.3 提取模型特征参数及对应的名称
coef = pipe_lasso.named_steps['lasso_regr'].coef_
# 提取对应的特征名称
features = x_train.columns.tolist()
# 构建参数df
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)
–> 输出的结果为:(被筛除的特征特征参数为0)
feature coefficient
0 area 27.032616
1 daypop 6.974273
2 nightpop -14.899314
3 night20-39 33.192064
4 sub_kde 0.000000
5 bus_kde 0.000000
6 kind_kde 0.000000
4.4 绘制参数柱状图
coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()
–> 输出的结果为:
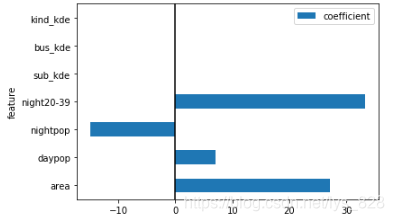
5 构建Ridge回归模型
废话不多说,直接开搞
5.1 加载模块、构造模型并拟合
与上面不同的是,这里又加了一个参数solver,也就是模型求解器,采用的方式为'lsqr'(最小二乘正交分解法)
from sklearn.linear_model import Ridge
# 构建ridge回归模型
pipe_ridge = Pipeline([('ridge_regr',Ridge(alpha=500, fit_intercept=True, solver = 'lsqr'))])
# 训练ridge回归模型
pipe_ridge.fit(x_train, y_train)
# 使用ridge回归模型进行预测
y_train_predict = pipe_ridge.predict(x_train)
5.2 查看线性模型特征参数和截距值
# 查看ridge回归模型特征参数
print(pipe_ridge.named_steps['ridge_regr'].coef_)
# 查看ridge回归模型截距值
print(pipe_ridge.named_steps['ridge_regr'].intercept_)
–> 输出的结果为:(与Lasso的区别可以发现,特征参数被约束接近于0,但不为0,b值差不多)
[ 27.12349221 7.01529213 -15.17165526 33.87360557 0.273439210.16398909 0.67896087]26056.944107140367
5.3 提取模型特征参数及对应的名称
# 提取模型特征参数
coef = pipe_ridge.named_steps['ridge_regr'].coef_
# 提取对应的特征名称
features = x_train.columns.tolist()
# 构建参数df
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)
–> 输出的结果为:
feature coefficient
0 area 27.123492
1 daypop 7.015292
2 nightpop -15.171655
3 night20-39 33.873606
4 sub_kde 0.273439
5 bus_kde 0.163989
6 kind_kde 0.678961
5.4 绘制参数柱状图
coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()
–> 输出的结果为:
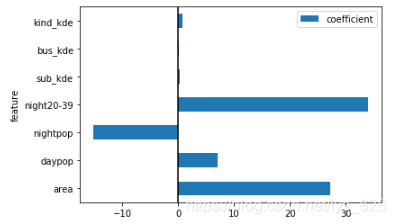
6. 构建logisti回归模型
6.1 加载模块、构造模型并拟合
还是一样加载Pipeline对象,将模型封装在里面,不同的是增加了参数penalty='l1',就是之前提到的L1正则系数,这次的求解器选择了'liblinear',也就是坐标下降法;(少数据量中选择坐标下降法, 大数据量下选择‘sag’或者'saga')
由于这里是分类的问题,最后训练的标签应该是类别型(y_label),而不再是之前的数值型(y_train)
# 加载logsti回归模型
from sklearn.linear_model import LogisticRegression
# 构建线性回归模型
pipe_logistic = Pipeline([('logistic_clf',LogisticRegression(penalty='l1', fit_intercept=True, solver='liblinear'))])
# 训练线性回归模型
pipe_logistic.fit(x_train, y_label)
# 使用线性回归模型进行预测
y_train_predict = pipe_logistic.predict(x_train)
逻辑回归模型参数解释 v0.21.3(2020/3/1) penalty(默认使用l2正则系数)
‘l1’: l1正则系数
‘l2’: l2正则系数
‘elasticnet’正则系数:只支持solver为’saga’
‘none’:无正则系数
solver(默认是’liblinear’:坐标下降法) ‘liblinear’:坐标下降法,可以处理了l1和l2正则系数,适用于小数据量(一般指10w个样本以下) ‘sag’:sag是随机平均梯度下降法,只能处理l2正则系数,适用于大数据量 ‘saga’: saga是sag的变体,能处理l1和l2正则系数,适用于大数据量
具体的一些讲解可以查询官网
6.2 查看线性模型特征参数和截距值
# 查看逻辑回归模型特征参数
print(pipe_logistic.named_steps['logistic_clf'].coef_)
# 查看逻辑回归模型截距值
print(pipe_logistic.named_steps['logistic_clf'].intercept_)
–> 输出的结果为:
[[-2.54246544e-03 8.50783993e-04 -4.65784667e-03 1.16522529e-029.62287062e+00 1.89063148e-01 1.41218313e+00]][-0.22713829]
5.3 提取模型特征参数及对应的名称
# 提取模型特征参数
coef = pipe_logistic.named_steps['logistic_clf'].coef_[0]
# 提取对应的特征名称
features = x_train.columns.tolist()
# 构建参数df
coef_table = pd.DataFrame({'feature': features, 'coefficient': coef})
print(coef_table)
–> 输出的结果为:(注意这里的coef变量,之前生成的列表都是一维的,这里是一维的,所以要索引第一个元素)
feature coefficient
0 area -0.002542
1 daypop 0.000851
2 nightpop -0.004658
3 night20-39 0.011652
4 sub_kde 9.622871
5 bus_kde 0.189063
6 kind_kde 1.412183
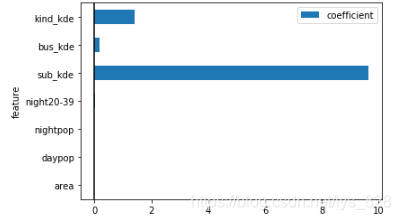
5.4 绘制参数柱状图
coef_table.set_index(['feature']).plot.barh()
# 设置x等于0的参考线
plt.axvline(0, color='k')
# 显示图表
plt.show()
–> 输出的结果为:
这篇关于【机器学习(5)】Scikit-learn创建线性回归模型(LinearRegression、Lasso及Ridge)和逻辑回归模型(logistic)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






