R语言有限混合模型聚类FMM、广义线性回归模型GLM混合应用分析威士忌市场和研究专利申请、支出数据

最近我们被客户要求撰写关于有限混合模型聚类的研究报告，包括一些图形和统计输出。

 【视频】KMEANS均值聚类和层次聚类：R语言分析生活幸福质量系数可视化实例

，时长06:05

摘要

有限混合模型是对未观察到的异质性建模或近似一般分布函数的流行方法。它们应用于许多不同的领域，例如天文学、生物学、医学或营销。本文给出了这些模型的概述以及许多应用示例。

相关视频：线性混合效应模型(LMM,Linear Mixed Models)和R语言实现

时长12:13

介绍

有限混合模型是对未观察到的异质性建模或近似一般分布函数的流行方法。它们应用于许多不同的领域，例如天文学、生物学、医学或营销。最近的专着 McLachlan 和 Peel (2000) 以及 Frühwirth-Schnatter (2006) 中给出了这些模型的概述以及许多应用示例。

有限混合模型

有限混合模型由 K 个不同分量的凸组合给出，即分量的权重为非负且总和为 1。对于每个组件，假设它遵循参数分布或由更复杂的模型给出，例如广义线性模型 (GLM)。下面我们考虑有限混合密度 h(·|·) 与 K 个分量、因变量 y 和（可选）自变量 x：

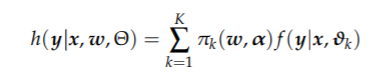
其中 ∀w, α：

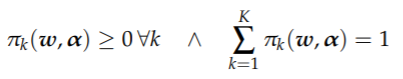
和

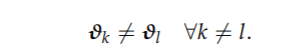
我们假设分量分布 f(·|·) 来自具有分量特定参数 ϑk 的相同分布族。分量权重或先验类别概率 πk 可选地取决于伴随变量 w 和参数 α，并通过多项 logit 模型进行建模，例如 Dayton 和 Macready (1988) 中的建议。McLachlan 和 Peel (2000, p. 145) 中也描述了类似的模型类。该模型可以使用 EM 算法（参见 Dempster 等人，1977 年；McLachlan 和 Peel，2000 年）进行 ML 估计或使用 MCMC 方法进行贝叶斯分析（参见例如 Frühwirth-Schnatter，2006 年）。

示例应用

下面我们将展示两个使用该包的示例。第一个示例演示基于模型的聚类，第二个示例给出了拟合广义线性回归模型的混合的应用。

基于模型的聚类

以下数据集参考了 Simmons 媒体和市场研究。它包含去年使用威士忌品牌的所有家庭，并提供了今年 21 个威士忌品牌的品牌使用情况的二元关联矩阵。我们首先加载包和数据集。威士忌数据集包含来自 2218 个家庭的观察结果。图 1 中给出了每个品牌的相对使用频率。提供了其他品牌信息，表明威士忌的类型：混合威士忌或单一麦芽威士忌。

R> set.seed(102)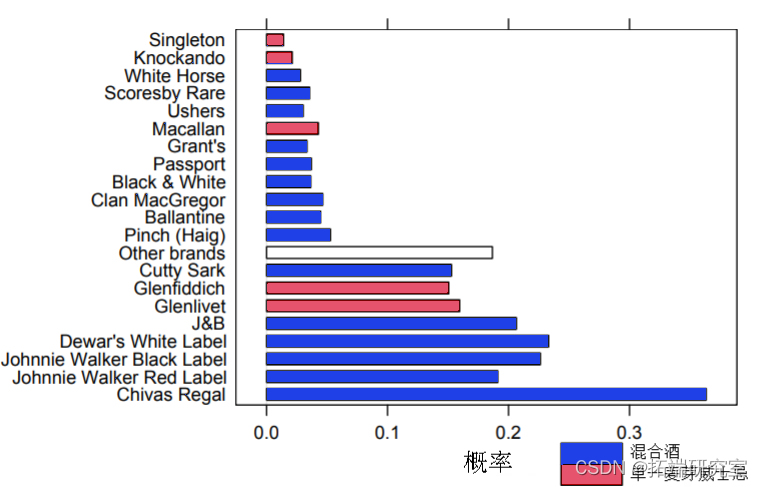

图 1：威士忌品牌的相对频率。

我们将二项式分布的混合拟合到数据集，其中假设每个组件特定模型中的变量是独立的。使用随机初始化将 EM 算法重复 3 次，即每个观察值分配给一个后验概率为 0.9 和 0.1 的成分，否则以相等的概率选择该成分。

mix(Ine ~ 1,
+ wets = ~ Freq, data = wey,
+ mol = FL,
+ conol = list(mior = 0.005),
+ k = 1:7, nrep = 3)

基于模型的聚类不使用解释变量，因此公式 Incidence ~ 1 的右侧是常数。我们改变 k = 1:7 的成分数量。关于每个不同数量成分的对数似然的最佳解决方案在类“stepFlexmix”的对象中返回。控制参数可用于控制 EM 算法的拟合。使用 minprior 指定成分的最小相对大小，在 EM 算法期间将删除低于此阈值的成分。

权重参数的使用允许仅使用唯一观察的数量进行拟合，这可以大大减少模型矩阵的大小，从而加快估计过程。对于这个数据集，这意味着模型矩阵有 484 行而不是 2218 行。可以使用信息标准进行模型选择，例如 BIC（参见 Fraley 和 Raftery，1998）。

R> BICbest <- Model(mix, "BIC")

可以使用诸如prior() 或parameters() 之类的函数来检查估计的参数。

R> priorR> parameters

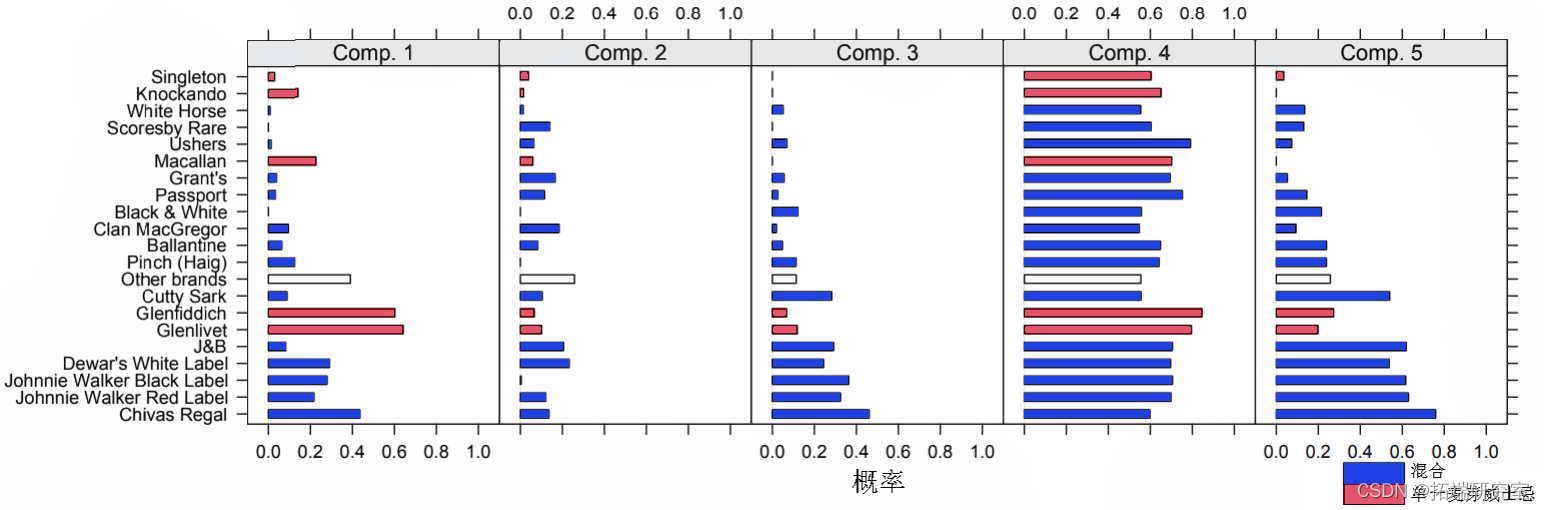
每种成分的混合物拟合参数如图 2 所示。可以看出，成分 4（占家庭的 1.1%）包含购买不同品牌数量最多的家庭，所有品牌的购买程度相似。来自第 5 成分的家庭 (8.5%) 也购买各种威士忌品牌，但倾向于避免单一麦芽威士忌。成分 3 (43.1%) 的使用模式与成分 5 相似，但总体上购买的品牌较少。成分 1 (14.2%) 似乎偏爱单一麦芽威士忌，成分 2 (33%) 尤其喜欢其他品牌，不喜欢尊尼获加黑标。

混合回归分析专利数据

专利数据包括从国家经济研究局的关于制药和生物医学公司的专利申请、研发支出和销售额（以百万元计）的 70 项观察结果。数据如图 3 所示。

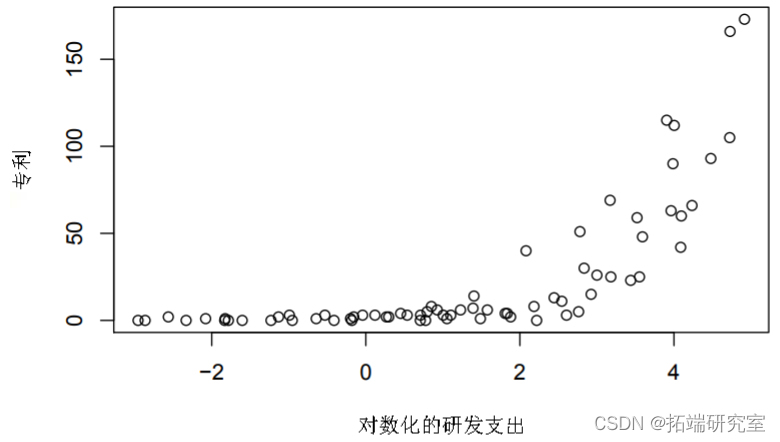
Wang等人选择的最佳模型(1998) 是三个泊松回归模型的有限混合，其中专利作为因变量，对数化​​的研发支出 lgRD 作为自变量，每个销售 RDS 的研发支出作为伴随变量。该模型可以使用特定于成分的模型驱动程序在 R 中拟合，拟合 GLM 的有限混合。作为伴随变量模型，用于多项 logit 模型，其中后验概率是因变量。

mix(Pats ~ RD,
+ k = 3, data ,
+ modlfaily = "poisson"),
+ coninom(~RS))

图 4 中给出了每个成分的观测值和拟合值。用于绘制观测值的颜色是根据使用最大后验概率的成分分配，这些概率是使用 聚类获得的。

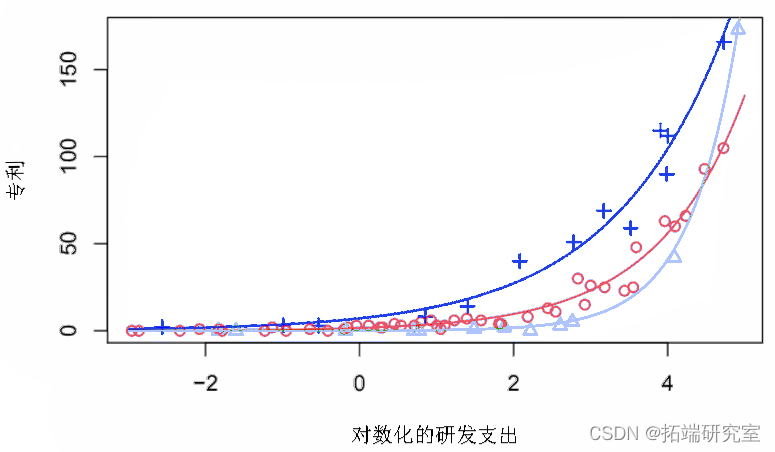
图 4：专利数据以及每个成分的拟合值。

在图 5 中给出了观测值的后验概率的根图。这是拟合函数返回的对象的默认图。它可用于任意混合模型，并指示混合对观察结果的聚类程度。为便于解释，后验概率小于 eps=10−4 的观察被省略。对于第三个分量的后验概率最大的观测值用不同的颜色着色。该图是使用以下命令生成的。

plot(pamix)

所有三个分量的后验都在 0 和 1 处具有模式，表明聚类分离良好（Leisch，2004）。

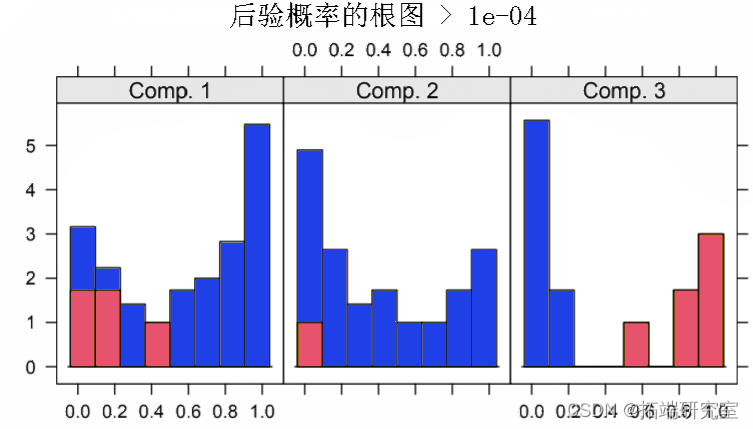
图 5：后验概率的根图。

可以获得拟合混合物的更多详细信息，返回拟合值以及近似标准偏差和显着性检验，参见图 6。标准偏差只是近似值，因为它们是为每个成分单独确定的，而不是采用考虑到成分已被同时估计。图 7 中给出了估计系数。黑线表示（近似的）95% 置信区间。

plot(refit, byclu = FALSE)

参数 cluster 指示成分或不同变量是否用作面板的条件变量。

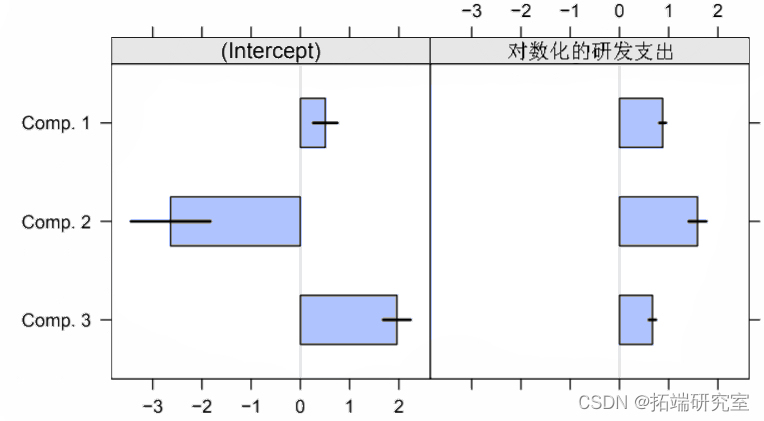
图 7：具有相应 95% 置信区间的成分特定模型的估计系数。

该图表明，即使第一个和第三个分量的 lgRD 系数相似，估计的系数在所有分量之间也有所不同。可以使用聚类参数的估计后验概率初始化 EM 算法。由于在这种情况下，第一个和第三个分量被限制为具有相同的 lgRD 系数，在重新排序分量以使这两个分量彼此相邻后，拟合混合的后验用于初始化。使用 BIC 将修改后的模型与原始模型进行比较。

fix(fam = "poisson",
+ nesd = list(k = c(1,2),
+ fora = ~lgRD))mix(Pats ~ 1,
+ cont = FLom(~RDS),
+ data , cluster

在这个例子中，原始模型是首选 被BIC选中。 

fit(patx)

概括

本文提供了使用 EM 算法拟合有限混合模型的基础方法，以及用于模型选择和模型诊断的工具。我们已经展示了该包在基于模型的聚类以及拟合有限混合模型回归分析方面的应用。将来，我们希望实现新的模型序，例如，用于具有平滑项的广义可加模型，以及扩展用于模型选择、诊断和模型验证的工具。