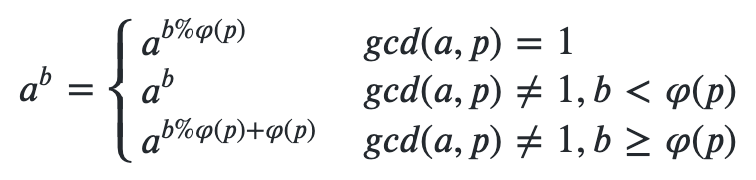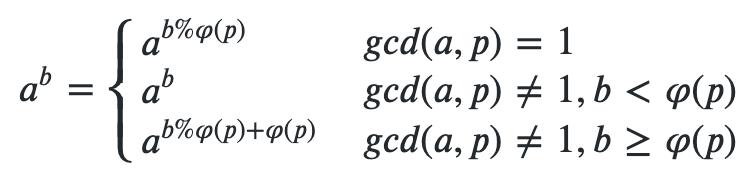广义专题
【机器学习】基扩展的基本概念以及其中的多项式回归、样条方法和广义可加模型的简单介绍（含python代码实例）
引言 基扩展是提升模型性能的重要工具，正确选择和应用基扩展方法可以显著提高模型的预测能力和解释性 文章目录 引言一、基扩展1.1 基扩展定义1.2 基扩展方法1.2.1 多项式基扩展1.2.2 样条基扩展1.2.3 径向基函数（RBF）1.2.4 傅里叶基扩展1.2.5 wavelet基扩展1.2.6 单隐藏层神经网络 1.3 应用场景1.4 使用基扩展的注意点 二、多项式回归2.
数据结构与算法 第四天（串、数组、广义表）
串（String） 任意字符组成的有限序列 串的类型定义 串的顺序存储结构 模式匹配算法 确定主串所含字串第一次出现的位置。 BF算法 穷举法，从每个字符开始依次匹配 KMP算法 链式存储 数组 基本操作 特殊矩阵存储 对称矩阵 三角矩阵 对角矩阵 稀疏矩阵 超过95%元素为零 三元组法 十字链表
【机器学习】广义线性模型和一般线性模型的联系和区别以及如何选择合适的链接函数
引言 广义线性模型（Generalized Linear Models，简称GLM）和一般线性模型（通常指的是线性回归模型）都是统计建模中常用的工具，但它们在假设、适用范围和模型结构上有所不同 文章目录 引言一、广义线性模型和一般线性模型的联系和区别1.1 联系1.1.1 线性预测器1.1.2 参数估计1.1.3 统计推断 1.2 区别1.2.1 响应变量的分布1.2.2 链接函数
软件设计师全套备考系列文章6 -- 线性表、栈和队列、串、数组、矩阵、广义表
软考-- 软件设计师（6）-- 线性表、栈和队列、串、数组、矩阵、广义表 文章目录 软考-- 软件设计师（6）-- 线性表、栈和队列、串、数组、矩阵、广义表前言一、线性表二、栈和队列三、串、数组、矩阵、广义表 前言 考试时间：每年5月、11月，软件设计师每年都会开考。考试条件：三不限考试形式： 一共两门上午--计算机于软件工程基本知识--150分钟--笔试--选择题
数据结构 第四章 串、数组和广义表
概述： 串：字符串的简称，串是一种特殊的线性表，特殊在其数据元素都是一个字符。 数组和广义表可以看做是线性表的扩充，即线性表的数据元素自身又是一个数据结构。 串 String 本结主要讲述：串的存储结构和基本操作 定义：主要是有0个或多个字符组成的序列。 存储结构：顺序存储和链式存储，但是串一般使用顺序存储结构。 顺序存储 typedef struct {char *ch; /
数据结构5---矩阵和广义表
一、矩阵的压缩存储 特殊矩阵:矩阵中很多值相同的元素并且它们的分布有一定的规律。 稀疏矩阵:矩阵中有很多零元素。压缩存储的基本思想是: (1)为多个值相同的元素只分配一个存储空间; (2)对零元素不分配存储空间。 1、特殊矩阵的压缩存储 （1）对称矩阵 只存储下三角部分的元素 存储结构 对于下三角的元素aij(i>=j)，在数组中的下标与
政安晨：【Keras机器学习示例演绎】（五十一）—— 利用广义网络、深度网络和交叉网络进行结构化数据学习
政安晨的个人主页：政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: TensorFlow与Keras机器学习实战 希望政安晨的博客能够对您有所裨益，如有不足之处，欢迎在评论区提出指正！ 本文目标：使用 "宽深 "和 "深交 "网络进行结构化数据分类。 目录 简介 数据集 设置 准备数据 定义数据集元数据 实验设置 创建模型输入 特征编码 实验 1：基线模型 实验 2：广
STAT315 Week 8 广义线性混合模型（GLMMs）
正如我们使用 LMM 对具有相关观测值的正态数据进行建模一样，我们可以使用 GLMM 对非正态分布且具有相关观测值的数据进行建模。 响应变量通常是离散的或明显非正态的。 GLMM 允许响应数据来自指数族的任何其他分布，包括最常见的二项分布和泊松分布。因此，GLMM 是具有正态分布随机效应的广义线性模型。 上图展示了广义线性混合模型（Generalized Linear Mixed Model
带你系统学习平滑样条、局部回归、广义可加性模型-豆瓣9.6分统计学神作ISL之第七章读书笔记（下）
目录 1.原文内容概要2.算法知识总结2.1 平滑样条（Smoothing Splines）2.1.1 平滑样条简介（An Overview of Smoothing Splines ）2.1.2 选择调优参数λ（Choosing the Smoothing Parameter λ） 2.2 局部回归（Local Regression）2.3 广义可加性模型（Generalized Addi
图和广义表_数据结构与算法
1.有向完全图 边数 = n(n-1) 无向完全图 边数 = n(n-1)/2 2.存储方式 a. 图的邻接矩阵 -> 数组； b. 链表：邻接表，邻接多重表，十字链表； 3.遍历方法 a. 深度优先遍历：递归 b. 广度优先遍历：队列 4.最小生成树 Prim算法：在与命中的顶点集相连的边中选一条权值最小的，再添加其顶点进顶点集；o(n[2]
二叉树的广义表反序列化
前言 个人小记 一、代码 #include<stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>#define MAX_NODE 10#define MAX_LEN 100#define key(n)(n)?(n->key):(-1)typedef struct Node{int key;struc
二叉树的序列化---广义表
前言 个人小记 一、代码 #include<stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>#define key(n) (n)?(n->key):(-1)#define MAX_NODE 10typedef struct Node{int key;struct Node* lchild,*rchi
【计算机视觉】Lecture 18：广义的立体视觉：对极几何
广义的立体视觉 主要思想：任何两张有重叠视图的图像，它们都可以被视为一对立体图像 我们只需要弄清楚这两个视图是如何关联的 视觉中一些最“漂亮”的数学问题是描述多个视图之间的几何关系。 回忆：对极约束（Epipolar Constraint） 重要的立体视觉概念： 给定左图像上的一个点，我们不必在整个右图像中搜索对应的点 “对极约束”将搜索空间缩小为一条一维的直线。 回顾：简单的立体
数据结构与算法学习笔记六--数组和广义表(C语言)
目录 前言 1.数组 1.定义 2.初始化 3.销毁 4.取值 5.设置值 6.完整代码 前言 这篇博客主要介绍数据结构中的数组和广义表的用法。 1.数组 在数据结构中，数组是一种线性数据结构，它由一组连续的相同类型的元素组成，每个元素都有一个唯一的索引或者下标来标识其在数组中的位置。 数字的常用操作除了初始
三种强大的物体识别算法——SIFT/SURF、haar特征、广义hough变换
转自：http://blog.csdn.net/cy513/article/details/4285579 SIFT/SURF基于灰度图（适用于：刚性物体，如建筑物） 一、首先建立图像金字塔，形成三维的图像空间，通过Hessian矩阵获取每一层的局部极大值，然后进行在极值点周围26个点进行NMS，从而得到粗略的特征点，再使用二次插值法得到精确特征点所在的层（尺度），即完成了尺度不
（三十三）第 5 章 数组和广义表（广义表的头尾链表存储表示实现 (SqString)）
1. 背景说明 2. 示例代码 1) errorRecord.h // 记录错误宏定义头文件#ifndef ERROR_RECORD_H#define ERROR_RECORD_H#include <stdio.h>#include <string.h>#include <stdint.h>// 从文件路径中提取文件名#define FILE_NAME(X) strr
（三十三）第 5 章 数组和广义表（广义表的头尾链表存储表示实现）
1. 背景说明 2. 示例代码 1) errorRecord.h // 记录错误宏定义头文件#ifndef ERROR_RECORD_H#define ERROR_RECORD_H#include <stdio.h>#include <string.h>#include <stdint.h>// 从文件路径中提取文件名#define FILE_NAME(X) strr
数据结构 习题 第五章 多维数组和广义表 （C语言描述）
最近在复习数据结构，所以想把平时上课做的习题做个总结，如果大家有遇到这方面的问题就可以参考一下了，废话不多说，直接开始吧。 1、单选题 稀疏矩阵一般的压缩存储方法有两种，即（ D） A. 二维数组和三维数组 B. 三元组表和散列 C. 散列和十字链表 D. 三元组表和十字链表 三元组表：将表示稀疏矩阵的非零元素的三元组表按行优先（或列优先）的顺序（跳过零元素），则得到一个其结点均是三元组的线
![[建图]基于贝叶斯广义核推理的可通行区域建图](https://img-blog.csdnimg.cn/20210421233649957.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1RyYXZpc19Y,size_16,color_FFFFFF,t_70#pic_center)
[建图]基于贝叶斯广义核推理的可通行区域建图
文章目录 一、简介二、原理三、项目演示四、总结参考 一、简介 可通行区域建图可以将可变高度地形的区域分类为可通行或不可通行，它可以解决崎岖地形和复杂结构化场景，是3D自主导航的有用工具。 相机、激光雷达或两者的组合通常用于地形的三维建图。尽管基于视觉的方法在提供密集点云上方面具有优势，但是它们对照明变化的敏感性可能会使获取的数据不可靠。但激光雷达可能夜间正常运行，且提供远距
第3章-从线性概率模型到广义线性模型(2)
简介 回顾上节文章中提到的logistic和probit模型： 我们假定了潜变量模型 y*=xβ+u (y=1，when y*>0; y=0，when y*<=0) 中的残差变量服从对应的是logistic分布或正态分布，并且我们假定 P ( y = 1 ∣ x ) = G ( β 0 + β 1 x 1 + β 2 x 2 + … + β n x n ) = G ( β 0 + x β )
2018湖南多校第一场 Exponial Gym - 101550E（广义欧拉降幂）
Everybody loves big numbers (if you do not, you might want to stop reading at this point). There are many ways of constructing really big numbers known to humankind, for instance: Exponentiation: 4
BZOJ3884. 上帝与集合的正确用法（欧拉定理,广义欧拉降幂）
Description 根据一些书上的记载，上帝的一次失败的创世经历是这样的： 第一天， 上帝创造了一个世界的基本元素，称做“元”。 第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。 第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。 第四天， 上帝创造了新的元素“γ”，
独家 | 在Python中使用广义极端学生化偏差（GESD）进行异常检测（附链接）
作者：Shaleen Swarup翻译：欧阳锦校对：王可汗本文约1700字，建议阅读5分钟本文从理论和实践角度介绍了使用广义极端学生化偏差（GESD）进行异常检测的方法，展示了Python代码示例和相关源码。 关键字：Python 异常值检测 ESD 图源: Unsplash 异常检测在生活中起着非常重要的作用。通常，异常数据可能与某种问题或罕见事件有关，例如 银行欺诈、医疗问题、结构缺