BZOJ3884. 上帝与集合的正确用法（欧拉定理,广义欧拉降幂）

本文主要是介绍BZOJ3884. 上帝与集合的正确用法（欧拉定理,广义欧拉降幂），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Description
根据一些书上的记载，上帝的一次失败的创世经历是这样的：
第一天，上帝创造了一个世界的基本元素，称做“元”。
第二天，上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。
第三天，上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。
第四天，上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。
如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。
然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……
然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。
至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？
上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。
你可以认为上帝从“α”到“θ”一共创造了10^{9次元素，或10}18次，或者干脆∞次。
一句话题意：

Input
接下来T行，每行一个正整数p，代表你需要取模的值
Output
T行，每行一个正整数，为答案对p取模后的值
Sample Input
3
2
3
6
Sample Output
0
1
4
Hint
对于100%的数据，T<=1000,p<=10^7

Source
By PoPoQQQ

思路：
欧拉定理：𝑎^𝜑(𝑛) ≡ 1(𝑚𝑜𝑑 𝑛) .
降幂公式
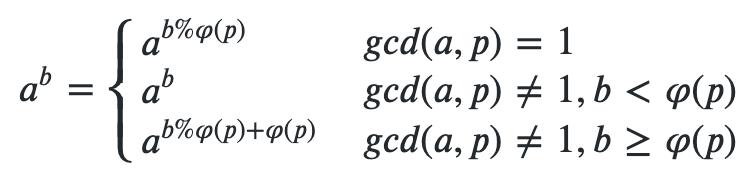
在这里插入图片描述
因为大于2的欧拉函数值均为偶数，所以一定满足降幂公式的第三条
定义 $f (p)$ 为模p时的答案，易知 $f (1) = 0$
$f (p) = 2$ ^2… (mod p) = 2^{2…mod𝜑(𝑝)+𝜑(𝑝)} = 2^{f(𝜑(𝑝))+𝜑(𝑝)}
递归地计算 $f$ 函数即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;typedef long long ll;ll qpow(ll x,ll n,ll mod)
{ll res = 1;while(n){if(n & 1)res = (res * x) % mod;x = x * x % mod;n >>= 1;}return res;
}ll phi(ll n)
{int m = (int)sqrt(n + 0.5);ll ans = n;for(int i = 2;i <= m;i++){if(n % i == 0){ans = ans / i * (i - 1);while(n % i == 0) n /= i;}}if(n > 1)ans = ans / n * (n - 1);return ans;
}ll f(ll p)
{if(p == 1) return 0;ll Phi = phi(p);return qpow(2,f(Phi) + Phi,p);
}int main()
{int T;scanf("%d",&T);while(T--){ll p;scanf("%lld",&p);printf("%lld\n",f(p));}return 0;
}