欧拉专题
uva 1342 欧拉定理(计算几何模板)
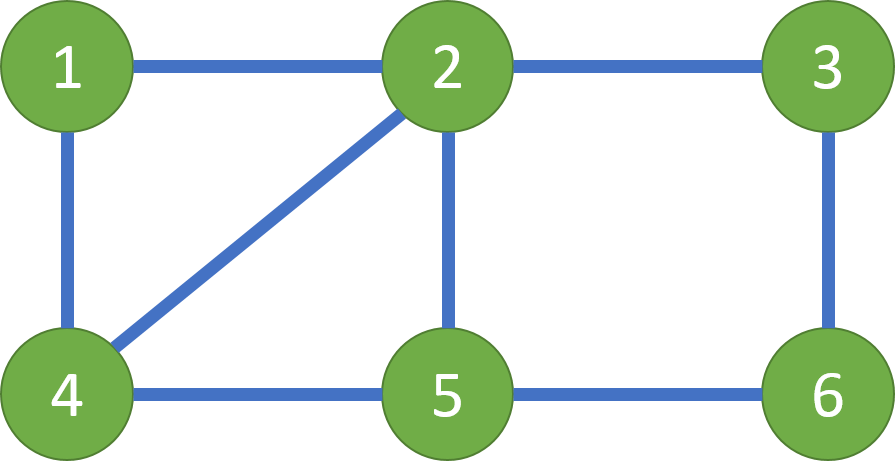
题意: 给几个点,把这几个点用直线连起来,求这些直线把平面分成了几个。 解析: 欧拉定理: 顶点数 + 面数 - 边数= 2。 代码: #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cstring>#include <cmath>#inc
欧拉系统 kernel 升级、降级
系统版本 cat /etc/os-release NAME="openEuler"VERSION="22.03 (LTS-SP1)"ID="openEuler"VERSION_ID="22.03"PRETTY_NAME="openEuler 22.03 (LTS-SP1)"ANSI_COLOR="0;31" 系统初始 kernel 版本 5.10.0-136.12.0.
nyoj99(并查集+欧拉路+dfs)
单词拼接 时间限制: 3000 ms | 内存限制: 65535 KB 难度: 5 描述 给你一些单词,请你判断能否把它们首尾串起来串成一串。 前一个单词的结尾应该与下一个单词的道字母相同。 如 aloha dog arachnid gopher tiger rat 可以拼接成:aloha.arachnid.dog.gopher.rat.tiger 输入 第一行是一个整
nyoj42(并查集解决欧拉回路)
一笔画问题 时间限制: 3000 ms | 内存限制: 65535 KB 难度: 4 描述 zyc从小就比较喜欢玩一些小游戏,其中就包括画一笔画,他想请你帮他写一个程序,判断一个图是否能够用一笔画下来。 规定,所有的边都只能画一次,不能重复画。 输入 第一行只有一个正整数N(N<=10)表示测试数据的组数。 每组测试数据的第一行有两个正整数P,Q(P<=1000,Q<
UVa 10820 Send a Table (Farey数列欧拉函数求和)
这里先说一下欧拉函数的求法 先说一下筛选素数的方法 void Get_Prime(){ /*筛选素数法*/for(int i = 0; i < N; i++) vis[i] = 1;vis[0] = vis[1] = 0;for(int i = 2; i * i < N; i++)if(vis[i]){for(int j = i * i; j < N; j += i)vis[j] =
JD 1027:欧拉回路
OJ题目:click here~~ 题目分析: 若图G中存在这样一条路径,使得它恰通过G中每条边一次,则称该路径为欧拉路径。若该路径是一个圈,则称为欧拉(Euler)回路。 具有欧拉路径的图称为欧拉图(简称E图)。 无向图存在欧拉回路的充要条件: 一个无向图存在欧拉回路,当且仅当该图拥有奇数度数的顶点的个数为0且该图是连通图。 有向图存在欧拉回路的充要条件: 一
欧拉数据库的搭建及其部署
数据库的搭建 进行数据库安装前,必须保证软件yum仓库搭建完成 使用命令 dnf install mariadb-server,发现冲突selinux-policy-targeted-35.5-21.oe2203sp3.noarch有问题 [root@localhost yum.repos.d]# dnf install mariadb-server [root@localhost yu
欧拉下搭建第三方软件仓库—docker
1.创建新的文件内容 切换目录到etc底下的yum.repos.d目录,创建docker-ce.repo文件 [root@localhost yum.repos.d]# cd /etc/yum.repos.d/ [root@localhost yum.repos.d]# vim docker-ce.repo 编辑文件,使用阿里源镜像源,镜像源在编辑中需要单独复制 https://mirr
【UVa】 10735 Euler Circuit 混合图的欧拉回路 最大流
题目链接:http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1676 题目要求:求混合图的欧拉回路+输出路径。 题目分析: 先看一段比较流行的说法吧~: -----------------------------------------
【HDU】5321 Beautiful Set【枚举k求贡献,欧拉函数应用】
传送门: 【HDU】5321 Beautiful Set my code: my~~code: #include <stdio.h>#include <string.h>#include <vector>#include <algorithm>using namespace std ;typedef long long LL ;#define clr( a , x ) memset
求素数的几个方法(最朴素版、n*sqrt(n)版、埃氏筛、欧拉筛)
最朴素版O(n^2) #include <bits/stdc++.h>using namespace std;int n, cnt, prim[6000000];bool flag; //true 表示质数int main(){scanf("%d", &n);for(int i=2; i<=n; ++i){flag=true; //默认为质数for(int j=2; j<=i-
HDU 1116(并查集,欧拉路径)
题意:给你一些英文单词,判断所有单词能不能连成一串,类似成语接龙的意思。但是如果有多个重复的单词时,也必须满足这样的条件才能算YES。否则都是不可能的情况。 解题思路: 欧拉路的基本题。只要知道就可以做出来了。 关于欧拉回路和欧拉路径 定义: 欧拉回路:每条边恰好只走一次,并能回到出发点的路径 欧拉路径:经过每一条边一次,但是不要求回到起始点 ①首先看欧拉回路存在性的判
HDU 1395(欧拉定理)
欧拉φ函数的值 通式:φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn),其中p1, p2……pn为x的所有质因数,x是不为0的整数。φ(1)=1(唯一和1互质的数(小于等于1)就是1本身)。 (注意:每种质因数只一个。比如12=2*2*3 欧拉公式 那么φ(12)=12*(1-1/2)*(1-1/3)=4 若n是质数p的k次幂,φ(n)=p^k
HIHO #1182 : 欧拉路·三(有向图 输出欧拉路径)
题目链接 A)建图是巧妙,使用边表示每一个数字,那么就是走完每一个边一次再回到起点,便是求欧拉回路 B)建图是有向图,建图需要注意,同时,输出的时候逆序输出 C)path保存的是完整的路径,输出的时候只需&1即可 #include<bits/stdc++.h>using namespace std;#define cl(a,b) memset(a,b,sizeof(a))#defin
HIHO #1181 : 欧拉路·二(fleury算法输出欧拉路径)
题目链接 伪代码 DFS(u):While (u存在未被删除的边e(u,v))删除边e(u,v)DFS(v)EndPathSize ← PathSize + 1Path[ PathSize ] ← u 点之间可能存在多条边,所以存边,然后标记每条边的标号,还是一个常见的存边的表示法 #include<bits/stdc++.h>using namespace std;#define c
从欧拉公式的美到旋转位置编码RoPE
也许你在某些场合听说过欧拉公式,也许你干脆对数学不感冒。机缘巧合下,你点开了这篇文章,大致浏览了下然后关闭,继续为自己的工作学习忙碌。这不妨碍你暂停忙碌的脚步,欣赏她的美。 若干年后,你应该不曾记得看过这篇文章,但你会记得数学界有一个很美的公式。 1. 欧拉公式和欧拉恒等式 欧拉公式(Euler’s formula)是复分析领域的公式,它将三角函数与复指数函数关联起来,因其提出者莱昂哈德·
poj 2154 Color(polya计数 + 欧拉函数优化)
http://poj.org/problem?id=2154 大致题意:由n个珠子,n种颜色,组成一个项链。要求不同的项链数目,旋转后一样的属于同一种,结果模p。 n个珠子应该有n种旋转置换,每种置换的循环个数为gcd(i,n)。如果直接枚举i,显然不行。但是我们可以缩小枚举的数目。改为枚举每个循环节的长度L,那么相应的循环节数是n/L。所以我们只需求出每个L有多少个i满足gcd(
poj 2478 Farey Sequence(基于素数筛法求欧拉函数)
http://poj.org/problem?id=2478 求欧拉函数的模板。 初涉欧拉函数,先学一学它基本的性质。 1.欧拉函数是求小于n且和n互质(包括1)的正整数的个数。记为φ(n)。 2.欧拉定理:若a与n互质,那么有a^φ(n) ≡ 1(mod n),经常用于求幂的模。 3.若p是一个质数,那么φ(p) = p-1,注意φ(1) = 1。 4.欧拉函数是积性函数:
hiho一下 第四十九周 欧拉路·一
【题目链接】:click here~~ 时间限制: 10000ms 单点时限: 1000ms 内存限制: 256MB 描述 小Hi和小Ho最近在玩一个解密类的游戏,他们需要控制角色在一片原始丛林里面探险,收集道具,并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N),以及连接小岛的M座木桥。每座木桥上各有一个宝箱,里面似乎装着什么
8.26 T2 日记和欧拉函数(欧拉函数)
http://cplusoj.com/d/senior/p/NOD2301B 发现 x ≤ B x\le B x≤B 时答案是 x x x x > B + 500 x>B+500 x>B+500 左右答案是1 我们预处理中间的就行 预处理直接暴力做,求 max ϕ \max \phi maxϕ 的话相当于求小于它的质数 #include<bits/stdc++.h>usin
COMSOL工业碱性电解槽(3D、双欧拉模型)
本案例通过改写COMSOL官方案例获得,使用了碱性电解槽和欧拉-欧拉(湍流)模型,阳极室和阴极室带有乳突状的结构,模型进行了人为缩小,仅供参考。其中一些参数可参考如下链接文章的说明。COMSOL碱性电解槽参数解读https://mp.csdn.net/mp_blog/creation/editor/141262489 1、物理参数,物理参数可参考官方案例“碱性电解槽”。 下列变量进
素数筛,单点的欧拉函数,筛法求欧拉函数
返回了在素数的个数、 int prime[maxn] , vis[maxn] ;int sieve(int n){int m = (int)sqrt(n+0.5) , i , j ;for(i = 2 ; i <= m ; i++)if( !vis[i] ) i{for(j = i*i ; j <= n ; j += i)vis[j] = 1 ;}j = 0 ;for(i
10054 - The Necklace(欧拉回路+回路打印)
题目:10054 - The Necklace 题目大意:给出N给珠子,每个珠子都有两种颜色,各半,看能不能找出每种组合使珠子连成一串,颜色相同的珠子才能相邻。 解题思路:欧拉回路+ 回路打印。 刚开始的时候我直接以珠子的个数来考虑是否有欧拉回路,这样的话1000*1000 *1000...次判断导致超时了。这里可以判断颜色,颜色都访问过了,就说明这串珠子是连通的。然后要输出的时
10129 - Play on Words(欧拉道路有向图)
题目:10129 - Play on Words 题目大意:词语接龙。 解题思路:刚开始没想到欧拉道路,直接找,结果超时了。 这题满足要求的话就是把每个单词看做一条路,每条路连在一起走一遍就符合要求, 欧拉回路也是符合要求的。 满足欧拉道路:1,至多只有两个点的出度入度相差1。 2, 这个有向图的无向图连通。(刚开始一直在想,如果有两条一样的路,这样怎么处理,后面