本文主要是介绍hiho一下 第四十九周 欧拉路·一,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【题目链接】:click here~~
-
6 8 1 2 1 4 2 4 2 5 2 3 3 6 4 5 5 6
样例输出 -
Full
描述
小Hi和小Ho最近在玩一个解密类的游戏,他们需要控制角色在一片原始丛林里面探险,收集道具,并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N),以及连接小岛的M座木桥。每座木桥上各有一个宝箱,里面似乎装着什么道具。
湖边还有一个船夫,船夫告诉主角。他可以载着主角到任意一个岛上,并且可以从任意一个岛上再载着主角回到湖边,但是主角只有一次来回的机会。同时船夫告诉主角,连接岛屿之间的木桥很脆弱,走过一次之后就会断掉。
因为不知道宝箱内有什么道具,小Hi和小Ho觉得如果能把所有的道具收集齐肯定是最好的,那么对于当前岛屿和木桥的情况,能否将所有道具收集齐呢?
举个例子,比如一个由6个小岛和8座桥组成的地图:
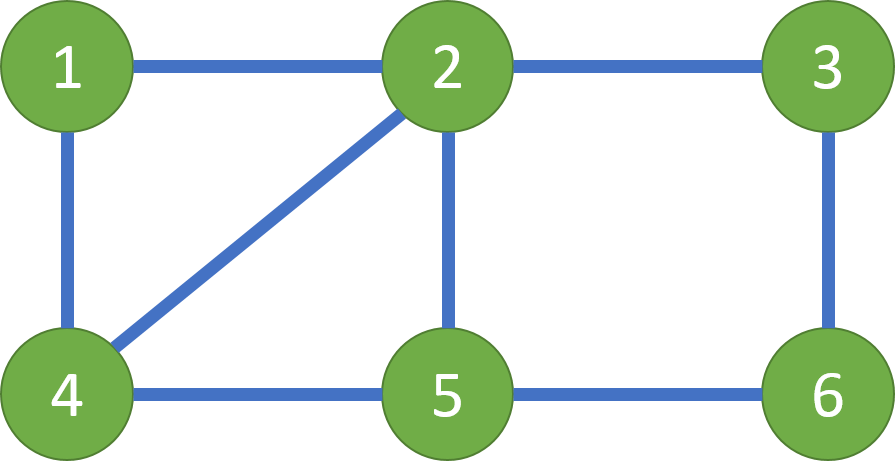
主角可以先到达4号小岛,然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛,然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。
提示:欧拉路的判定
输入
第1行:2个正整数,N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000,1≤M≤50,000
第2..M+1行:每行2个整数,u,v。表示有一座木桥连接着编号为u和编号为v的岛屿,两个岛之间可能有多座桥。1≤u,v≤N
输出
第1行:1个字符串,如果能收集齐所有的道具输出“Full”,否则输出”Part”。
欧拉路是有判定条件的:一个无向图存在欧拉路当且仅当该图是连通的且有且只有2个点的度数是奇数,此时这两个点只能作为欧拉路径的起点和终点。
若图中没有奇数度的点,那么起点和终点一定是同一个点,这样的欧拉路叫做欧拉回路,但是别忘了最重要的一点,需要整个图是连通的。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int t,n,k,m,x;
int father[N],indegree[N];
int Find(int x)
{if(x==father[x]) return x;return father[x]=Find(father[x]);
}
bool is_eular()
{int cnt=1,ans=0;for(int i=1; i<=n; i++){if(father[i]==i) cnt--;}if(cnt!=0) return false;//图不通for(int i=1; i<=n; i++){
//奇数度的点至多只能有2个。一个无向图存在欧拉路当且仅当该图是连通的且有且只有2个点的度数是奇数,
//此时这两个点只能作为欧拉路径的起点和终点。if(indegree[i]&1){ ans++;if(ans>2) return false;}}return true;
}
int main()
{int u,v;while(scanf("%d%d",&n,&m)!=EOF){for(int i=1; i<=n; i++) father[i]=i;while(m--){scanf("%d%d",&v,&u);indegree[v]++;indegree[u]++;int fav=Find(v);int fau=Find(u);if(fav!=fau){fav>fau?(father[fav]=fau):(father[fau]=fav);}}if(is_eular()) puts("Full");else puts("Part");}return 0;
}
/*
6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6
*/
这篇关于hiho一下 第四十九周 欧拉路·一的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




