2018湖南多校第一场 Exponial Gym - 101550E（广义欧拉降幂）

本文主要是介绍2018湖南多校第一场 Exponial Gym - 101550E（广义欧拉降幂），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Everybody loves big numbers (if you do not, you might want to stop reading at this point). There are many ways of constructing really big numbers known to humankind, for instance:

Exponentiation: $42^{2016}= \underbrace{ 42 \cdot 42 \cdot ... \cdot 42 }_{2016\ times}$ .
Factorials: 2016!=2016 ⋅ 2015 ⋅ … ⋅ 2 ⋅ 1.
Illustration of exponial(3) (not to scale), Picture by C.M. de Talleyrand-Périgord via Wikimedia Commons

In this problem we look at their lesser-known love-child the exponial, which is an operation defined for all positive integers n as
exponial(n)=n(n − 1)(n − 2)⋯21
For example, exponial(1)=1 and exponial(5)=54321 ≈ 6.206 ⋅ 10183230 which is already pretty big. Note that exponentiation is right-associative: abc = a(bc).

Since the exponials are really big, they can be a bit unwieldy to work with. Therefore we would like you to write a program which computes exponial(n) mod m (the remainder of exponial(n) when dividing by m).

Input
There will be several test cases. For the each case, the input consists of two integers n (1 ≤ n ≤ 109) and m (1 ≤ m ≤ 109).

Output
Output a single integer, the value of exponial(n) mod m.

Sample Input
2 42
5 123456789
94 265
Sample Output
2
16317634
39

题意：
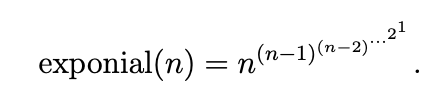
在这里插入图片描述
求这玩意。

思路；
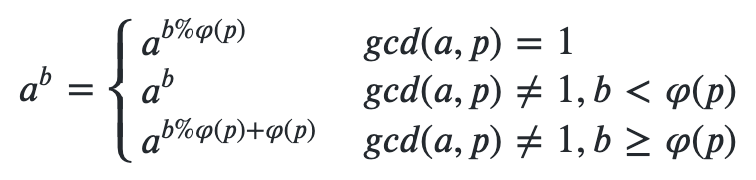
在这里插入图片描述
再次祭出广义欧拉降幂式子。

和BZOJ3884. 上帝与集合的正确用法差不多。
我们定义 $f (n, m)$ 为模m下的exponial式子值。
那么可以可以有
f(n,1) = 0
f(n,m) = f(m^{f(n-1,m)mod𝜑(𝑝)+𝜑(𝑝)},m)

但是注意欧拉降幂中第三个式子的使用条件是 $b \geq p h i (p)$
当n = 4的时候已经是 2¹⁸了，n = 5的时候值一定是大于m的，所以我们特判n ≤ 4时候的情况。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;typedef long long ll;ll qpow(ll x,ll n,ll mod)
{ll res = 1;while(n){if(n & 1)res = (res * x) % mod;x = x * x % mod;n >>= 1;}return res;
}ll phi(ll n)
{int m = (int)sqrt(n + 0.5);ll ans = n;for(int i = 2;i <= m;i++){if(n % i == 0){ans = ans / i * (i - 1);while(n % i == 0) n /= i;}}if(n > 1)ans = ans / n * (n - 1);return ans;
}ll f(ll n,ll m)
{if(m == 1) return 0;if(n == 1) return 1;if(n == 2) return 2 % m;if(n == 3) return 9 % m;if(n == 4) return qpow(4,9,m);ll phip = phi(m);ll k = f(n - 1,phip) % phip + phip;return qpow(n,k,m);
}int main()
{ll n,m;scanf("%lld%lld",&n,&m);printf("%lld\n",f(n,m));return 0;
}