带你系统学习平滑样条、局部回归、广义可加性模型-豆瓣9.6分统计学神作ISL之第七章读书笔记（下）

本文主要是介绍带你系统学习平滑样条、局部回归、广义可加性模型-豆瓣9.6分统计学神作ISL之第七章读书笔记（下），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.原文内容概要

第七章读书笔记【上】已系统介绍了多项式回归、阶梯函数、基函数和回归样条（有兴趣的同学可以看以往的读书笔记）。这次的读书笔记，主要集中在平滑样条、局部回归、广义可加性模型。

2.算法知识总结

2.1 平滑样条（Smoothing Splines）

前面我们构造样条函数的方式大致分为以下三步：
1）首先确定结点的数量和放置位置（specifying a set of knots）；
2）然后设置一系列基础函数来转换原始自变量（producing a sequence of basis functions），用以表示样条模型的内涵；
3）最后通过最小二乘法来拟合参数（using least squares to estimate the spline coefficients）。
在这一节中，我们将采用一种全新的方式来得到样条函数。

2.1.1 平滑样条简介（An Overview of Smoothing Splines ）

我们在拟合数据时，实际上所做的是寻找一个函数$g(x)$，使得这个函数产生的预测值尽可能接近样本因变量的真实值，也就是尽可能减小残差平方和 $RSS={\sum }_{i=1}^n(y_i-g(x_i){)}^2$。但如果我们不对模型加以任何限制，这个目标会导致模型最终变得过度拟合（overfitting）。因此，为了使模型更加平滑（smooth），我们加入了一个限制条件，原先的目标函数就变成：

上面这个目标函数是典型的“Loss（损失函数）+ Penalty（惩罚项）”的组合，其中损失函数旨在使模型尽可能拟合训练数据，而惩罚项则用于防止模型过拟合，体现了平衡（trade-off）的思想。$g^{\prime \prime }(t)$表示函数$g$在$x=t$位置的二阶导数。一阶导数代表函数的斜率，而二阶导数代表斜率的变化率，因此二阶导数可以作为衡量函数光滑程度（roughness）的指标，即其非线性的程度。$g^{\prime \prime }(t{)}^2$（平方确保惩罚项为正）的大小反映了函数$g$在$x=t$附近的复杂度，值越大表明函数在该处越“蜿蜒曲折”，因而将受到更大的惩罚。积分符号$\int$表示对函数进行整体求和，于是$\int g^{\prime \prime }(t{)}^{2}dt$量化了在整个自变量范围内$g^{\prime }(t)$的总变化。若函数$g$较平滑，则$g^{\prime }(t)$变化小，接近常数，使得$\int g^{\prime \prime }(t{)}^{2}dt$的值降低。在极端情况下，如果函数$g$是完全线性的（最理想的平滑情况），那么$g^{\prime }(t)$是常数，$g^{\prime \prime }(t)$将为零。

这里的$\lambda$是非负的调优参数（tuning parameter），与lasso和ridge回归中的目标函数中的$\lambda$是相同的概念。这里的$g(x)$我们称之为平滑样条函数（smoothing spline）。

仔细思考这个函数$g$，实际上它是一个分段的三阶多项式回归模型（结点为$x_1,\dots ,x_n$），并且附加了在每个结点处一阶和二阶可导的限制条件（it is a piecewise cubic polynomial with knots at the unique values of $x_1,...,x_n$, and continuous first and second derivatives at each knot）。换句话说，它就是一个结点为$x_1,\dots ,x_n$的自然三阶样条函数（a natural cubic spline with knots at $x_1,\dots ,x_n$），并且还是一个具有自由调节压缩程度（a shrunken version）的版本，这是由于$\lambda$的存在。之所以称之为平滑样条（smoothing spline），而不是直接叫做自然样条（natural spline），是因为在平滑样条中，$x$的每一个值（$x_1,\dots ,x_n$）都被当作了结点。

2.1.2 选择调优参数λ（Choosing the Smoothing Parameter λ）

既然在平滑样条函数中，每个点都作为结点，那么模型的自由度可能会高得上天（It might seem that a smoothing spline will have far too many degrees of freedom, since a knot at each data point allows a great deal of flexibility）。幸运的是，目标函数中的惩罚项起到了平衡的作用，使得最终的自由度（我们称之为有效自由度（effective degrees of freedom），记作 $d{f}_{\lambda }$ ）并不会过高，其中调优参数 $\lambda$ 扮演了至关重要的角色。实践证明，当$\lambda$从0增大到正无穷时，$d{f}_{\lambda }$的数值会从等于样本量$n$下降到2。

我们在这里讨论有效自由度的原因是，在普通情况下自由度等同于模型中独立自变量的数量（例如线性回归、多项式回归等）（Usually degrees of freedom refer to the number of free parameters, such as the number of coefficients fit in a polynomial or cubic spline）。然而，在平滑样条、岭回归等使用了正则化技术的情况下，这些独立自变量对模型的影响受到了调优参数$\lambda$显著的限制。因此，我们不能简单地将自由度与独立自变量的数量等同起来。所以我们特别使用$d{f}_{\lambda }$来表示平滑样条的非线性程度（灵活性）。

关于如何确定有效自由度，一种方法是预估法，即通过计算平滑矩阵（smoothing matrix），求得该矩阵对角线元素之和，这个和就是预估的有效自由度（这里不展开讲述什么是平滑矩阵，因为那是一个非常专业的话题）。当然，另一种更简单的方法是直接应用交叉验证（cross-validation）。

与之前讨论的回归样条（regression spline）相比，由于在平滑样条（smoothing spline）中我们默认每个自变量$X$的值都是结点（knot），这样就避免了确定节点数量和位置的问题。然而，新的问题是如何确定调优参数$\lambda$。显然，我们会使用交叉验证的方法来选择$\lambda$值，使得交叉验证的残差平方和（RSS）尽可能小。作者特别强调了留一法（leave-one-out cross-validation, LOOCV）对于平滑样条效率的优势（具体原因太技术了，作者没有展开讲，只要记住这个结论就行）。

下图展示了两个平滑样条函数，其中一个具有16个自由度，这是作者主观决定的；另一个具有6.8个自由度，这是通过留一法交叉验证（LOOCV）确定的。我们可以看到两条曲线比较接近。根据尽量降低模型复杂度的原则，我们会选择使用自由度为6.8的模型。

2.2 局部回归（Local Regression）

局部回归的思路非常独特：它不是直接对整个训练样本集进行拟合，而是针对样本集中的每一个点，先划定一个范围，然后只对这个范围内的样本点进行拟合（Local regression is a different approach for fitting flexible non-linear functions, which involves computing the fit at a target point$x_0$using only the nearby training observations）。这样一来，在每个样本点的周围，都会存在一个独立的拟合模型。最终，这些模型彼此连接起来，形成了一条完整的曲线。这也是它被称为“局部”（local）回归的原因。

具体的算法流程如下，以$x_0$处的拟合为例说明：
1）选择一个数值$k$，它表示距离$x_0$最近的$k$个样本点，即定义邻域的大小；
2）根据样本点与$x_0$的距离远近，为这$k$个样本点分配权重，记作$K_{i0}=K(x_i,x_0)$，其中$i$是样本点的索引。样本点越靠近$x_0$，其权重越大。对于不在最近$k$个样本点范围内的其他样本点，它们的权重全部设为0；
3）使用上一步骤中确定的权重进行加权最小二乘回归分析。有些同学可能不清楚加权是如何实现的。实际上，它是通过在残差平方和（RSS）的目标函数中乘以权重$K_{i0}$来体现的。距离$x_0$更近的点具有更高的权重$K_{i0}$，这意味着它们在拟合过程中的重要性更大。因此，模型需要更精细地拟合这些点，否则由于$K_{i0}$的值较大，即使很小的偏差也会导致较大的惩罚。相反，如果一个点的权重是0，那么即使模型没有拟合该点，也不会受到任何惩罚；

4）将上一步拟合得到的模型代入$x_0$，得到该点的拟合值。

为了拟合局部回归模型，我们需要做出以下决策 ：
1）确定权重函数 $K$：选择一个合适的权重函数$K$，它用于在拟合过程中为不同样本点分配权重。
2）选择基础模型：决定在局部拟合中使用的模型类型，例如线性函数、多项式函数等。上文算法示例中使用了线性函数作为例子。
3）选择领域大小：确定参与局部模型拟合的样本数量，这与$K$最近邻（KNN）中的$K$相似。通常使用比例$s$（span）来表示，等于“每次参与拟合的样本数”除以“总样本数”。这个值用于控制局部回归模型的复杂度。$s$的值越大，模型越平滑；$s$的值越小，模型越复杂。换句话说，$s$值较小会导致拟合更加局部化和波动；而$s$值较大则会导致使用所有训练观测值对数据进行全局拟合。我们可以使用交叉验证来确定这个参数的合理值。

从下面的图就可以看出，s越小，函数越“蜿蜒曲折”。

当数据集包含多个特征（例如$X_1,X_2,\dots ,X_p$）时，局部回归的概念可以扩展应用。具体而言，我们可以在部分变量上采用全局拟合（即使用全部数据集进行模型拟合），同时在其他变量上实施局部拟合。举个例子，“时间”可能被视为一个需要局部拟合的变量，而其他特征则可能需要全局拟合。这样的模型设计使我们能够灵活地适配数据中的变化，尤其是当数据随时间或其他因素展现出动态变化时。

需要注意的是，在大多数情况下，当局部回归涉及的自变量超过3到4个时，其性能可能会显著下降。这是因为在高维空间中，找到与目标点邻近的点变得更加困难，这种现象有时被称为“维数灾难”（However, local regression can perform poorly if p is much larger than about 3 or 4 because there will generally be very few training observations close to $x_0$）。类似地，我们在第三章讨论的KNN回归算法也受到这个限制的影响，因为在高维特征空间中，数据点之间的密度迅速减小，导致难以找到足够的邻近点来进行有效的局部拟合。

2.3 广义可加性模型（Generalized Additive Models）

再次提醒大家，到目前为止，前面我们讨论的模型场景都是单变量的情况，因此可以将前面的模型视为普通一元线性回归模型的扩展（These approaches can be seen as extensions of simple linear regression）。在本节中，我们将讨论多变量情况，这相当于对普通多元线性回归模型的扩展（This amounts to an extension of multiple linear regression）。

广义加性模型（Generalized Additive Models，简称GAMs）是一种灵活的统计建模方法，可视为传统线性模型的扩展。GAMs的特点是允许每个特征通过非线性函数来更有效地捕捉数据中的复杂模式，尤其是在处理具有非线性关系或阶段性变化的数据时表现出色。同时，GAMs保持了模型的可加性特性（如果需要回顾可加性的定义，可以参阅第三章（下）的读书笔记）。GAMs既可以用于回归分析，也可以应用于分类问题。

2.3.1 回归问题（GAMs for Regression Problems）

这是普通的多元线性回归模型：

为了将模型升级到GAMs，一个直观而有效的方法是将模型中的线性项${\beta }_j{x}_{ij}$替换为$f_j(x_{ij})$，其中$f_j(\cdot )$表示非线性的转换函数（可以认为是平滑函数）。通过这样的替换，传统的多元线性模型便演变为以下形式的GAM：

之所以称这个模型为可加模型，是因为我们对每个自变量分别定义了其非线性转换函数$f_j(\cdot )$，然后能够简单地将这些非线性函数的预测结果相加，以获得最终的预测值（It is called an additive model because we calculate a separate $f_j$ for each $X_j$, and then add together all of their contributions）。

对于GAMs而言，之前讨论的方法都可以被视为构建模型的积木块。GAMs提供了灵活性，允许我们根据需要组合这些积木块，以搭建出符合我们需求的定制模型（The beauty of GAMs is that we can use these methods as building blocks for fitting an additive model）。

考虑拟合以下方程，其中工资（wage）、年份（year）和年龄（age）是连续变量，教育水平（education）是离散变量。我们定义$f_1$和$f_2$为自然样条函数，而$f_3$定义为哑变量函数。拟合此模型的方法仍然使用最小二乘法。由于自然样条函数可以表示为一系列基函数，正如前面所讨论的，因此整个模型可以被看作是一个具有多个转换变量的大型回归模型。


下图展示了拟合结果的可视化。解读这些图表的方式与之前的线性回归图类似。以最左边的图表为例，它显示了在假定年龄和教育水平不变的情况下，工资随年份增长的趋势。这种缓慢的增长可能是由通货膨胀导致的。

作者提到，在GAM中使用平滑样条（smoothing spline）比使用自然样条（natural spline）更难拟合，因为平滑样条不能通过最小二乘法来直接拟合，由于有惩罚项的存在。有一种叫backfitting方法可以用来拟合基于平滑样条的GAM，但具体的拟合过程较为复杂，已经超出了本书的讨论范围，大家可以暂时忽略这一部分。目前主流的机器学习库已经对这个方法进行了封装，方便使用。

2.3.2 分类问题（GAMs for Classification Problems）

与回归问题的处理方法详相似。标准的逻辑回归模型如下所示：


加入非线性的转换函数后，变成如下形式：


代入工资数据集后，具象化后的模型表达式为：


其中：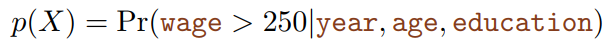

下图可视化展示了拟合的结果：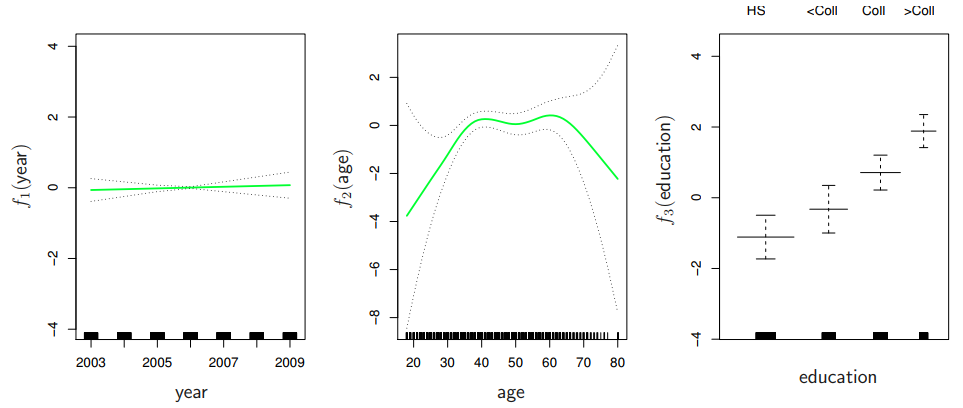

2.3.3 优缺点（Pros and Cons of GAMs）

优点：
1）能够帮助我们自动拟合非线性关系，无需手动对每个变量进行变换尝试（GAMs allow us to fit a non-linear $f_j$ to each $X_j$, so that we can automatically model non-linear relationships that standard linear regression will miss）；
2）因为模型具有可加性，我们能够洞察每个自变量与因变量之间的具体关系（Because the model is additive, we can examine the effect of each $X_j$ on $Y$ individually while holding all of the other variables fixed）；
3）可以通过调整自由度参数来直接控制函数的$f$非线性程度（The smoothness of the function $f_j$ for the variable $X_j$ can be summarized via degrees of freedom）。

缺点：
1）由于GAMs的可加性限制，单纯的GAMs会忽略变量之间的相互作用（The main limitation of GAMs is that the model is restricted to be additive. With many variables, important interactions can be missed）。为了弥补这一缺陷，我们可以自行尝试引入交互项，但这需要我们进行预先的判断，无法完全依赖模型自身去发掘这些关系。

综上，GAMs提供了一种介于线性模型和完全非参数模型（如KNN，随机森林等）之间的选择（GAMs provide a useful compromise between linear and fully nonparametric models）。它们既能实现对非线性关系的拟合，又能在一定程度上保持模型的可解释性。

引用

这篇关于带你系统学习平滑样条、局部回归、广义可加性模型-豆瓣9.6分统计学神作ISL之第七章读书笔记（下）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---