第3章-从线性概率模型到广义线性模型(2)

本文主要是介绍第3章-从线性概率模型到广义线性模型(2)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

简介

回顾上节文章中提到的logistic和probit模型：

我们假定了潜变量模型
y*=xβ+u
(y=1，when y*>0; y=0，when y*<=0)
中的残差变量服从对应的是logistic分布或正态分布，并且我们假定
$P(y=1|x)=G({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_n{x}_n)=G({\beta }_0+x\beta )=G(x\beta )$
的变换函数G()为对应的"标准的Logistic随机变量的累计分布函数"或
“标准的正态随机变量的累计分布函数”。

那么这两个模型的因变量都是离散的或者说是定性( or 分类)变量。
这类变量除了第一节讨论的名义变量中的二元变量外，还有下面三种形式：

• 名义变量中的多元变量
• 定序变量
• 计数变量

备注：
1，由0-1二元变量的期望等于P(Y=1|x)的概率可知，我们的研究问题也可以是针对因变量为概率型
2，对于因变量为数据值的数据，也是可以分组为上述几种离散数据的形式的
3，对于因变量的意义为“占比”时，可以转换为计数问题
4，根据变量的层级关系：名义变量<定序变量 <计数或者说间隔变量，我们的模型适用情况如下，低层的模型可以适用于高层，反之不成立。举例说明，针对名义变量设计出来模型可以适用于定序变量，但是针对定序变量设计出来的模型不适用于名义变量。但是要记住一点，这种跨层级模型使用方式并不是最优的，因为模型并没有充分利用数据中的信息。

接下来，我们思考，并学习：
1，如果残差不服从logistics分布或正态分布，而服从其他分布时的情况
2，变换函数，除了logit变换，还有其他的变换形式时的情况
3，有没有一种能够概括这些模型的统一方法

正文

一，我们先来回归一些常用的离散变量的概率分布

1，伯努利分布(0-1分布)

$Pr(x=1)=p,Pr(x=0)=1-p,0<p<1$
$E(x)=p$
$D(x)=p(1-p)$

例子：扔硬币正面朝上的概率	

2，二项分布

二项分布是n次独立的伯努利试验。

$P(x=k)=$$\left(\begin{array}{c}n\\ k\end{array}\right)p^k(1-p{)}^{n-k}=b(k;n,p)$
$E(x)=np$
$D(x)=np(1-p)$

np之积>5时，分布近似正态分布
例子：扔硬币k次正面朝上的概率p

3，多项分布

多项式分布是二项式分布的推广 ，把二项分布公式推广至多种状态，就得到了多项分布。

某随机实验如果有k个可能结局$A_1、A_2、\dots 、A_k$，分别将他们的出现次数记为随机变量$X_1、X_2、\dots 、X_k$，它们的概率分布分别是$p_1，p_2，\dots ，p_k$，那么在n次采样的总结果中，$A_1$出现$n_1$次、$A_2$出现$n_2次、\dots 、A_k$出现$n_k$次的这种事件的出现概率P有下面公式：

$P(X_1=n_1,X_2=n_2,...,X_k=n_k)=\frac{n!}{n_1!n_2!...n_k!}{p}_1^{n_1}{p}_2^{n_2}...p_k^{n_k},{\sum }_{i=1}^k{n_i}_{=}n$

$E[n_i]=n{p}_i$
$D[n_i]=n{p}_i(1-p_i)$

例子：扔骰子，k次中均由其中一个面(比如说点数6)朝上的概率

4，负二项分布

二项分布从状态上扩展，即为多项分布，从试验成功的次数上来研究，即拓展为负二项分布。

已知一个事件在伯努利试验中每次的出现概率是$p$，在一连串伯努利试验中，一件事件刚好在第$r+k$次试验出现第$r$次的概率。（当r是整数时，负二项分布又称帕斯卡分布）。

若$X=k$表示在第r次成功之前，失败的次数，则

$Pr(x=k)=$$\left(\begin{array}{c}r+k-1\\ k\end{array}\right)p^r(1-p{)}^k=f(k;r,p)$

$E(x)=\frac{r(1-p)}{p}$

$D(x)=\frac{r(1-p)}{p^2}$

例子：扔硬币，刚好在第r+k次试验出现第r次正面朝上的概率

5，泊松分布

在二项分布的基础上，如果$n\to \infty$，$p=\frac{\lambda }{n}\to 0时，则极限结果为泊松分布。$

$P(X=x)=\frac{{\lambda }^x}{x!}{e}^{-\lambda }$

$E(x)=D(x)=\lambda$

X:一定时间或空间内，稀有事件发生的个数，一般服从泊松分布
当二项分布的p很小，n很大时，极限分布为泊松分布
当然，二项分布、泊松分布与正态分布之间都有关系，

参见

5.1 泊松分布的：overdispersion
我们知道，理论上，泊松分布的期望和方差是相等的，但此时若观测到的样本方差系统地大于分布假设下的方差，就出现了所谓的 “超散布性”(overdispersion)，类似地，若出现方差偏小的情况，也就相应出现了 “超聚集性”(underdispersion)。

5.2 当泊松分布出现overdispersion现象时，通常可以转换成使用负二项分布进行建模。
负二项分布可以看成是广义的泊松分布，它可由 X|λ∼Poisson(λ) 且 λ∼Gamma(α,β)，推导得到。

(1) 如果，$X|\lambda \sim Poisson(\lambda )，则f(x|\lambda )=Pr(X=x|\lambda )=\frac{{\lambda }^x{e}^{-\lambda }}{x!}$
(2) 且， $\lambda \sim Gamma(\alpha ,\beta )，则f(\lambda )=\frac{a^{\beta }}{Г(\beta )}{\lambda }^{\beta -1}{e}^{-a\lambda }$
(3) 我们可以得到，联合概率
$Pr(X=x|\lambda )Pr(\lambda )$

$=\frac{{\lambda }^x{e}^{-\lambda }}{x!}\ast \frac{a^{\beta }}{Г(\beta )}{\lambda }^{\beta -1}{e}^{-a\lambda }$

$=\frac{a^{\beta }}{x!•Г(\beta )}{\lambda }^{x+\beta -1}{e}^{-(a+1)\lambda }$

则，x的边际分布即为负二项分布：

$Pr(X=x)=\frac{a^{\beta }}{x!•Г(\beta )}{\int }_0^{\infty }{\lambda }^{x+\beta -1}{e}^{-(a+1)\lambda }d\lambda$
$=C_{n+\beta -1}^n(\frac{a}{a+1}{)}^{\beta }(\frac{1}{a+1}{)}^n$

表示，第r=β次成功的负二项分布，且成功的概率为 $p=\frac{a}{a+1}$，

6，引入先验信息

二项分布或多项分布中，随机事件发生的概率是固定的，但是如果对于总体中的不同个体，，随机事件发生是概率是不同时，在贝叶斯研究体系下，我们就可以引入先验概率对不同个体的发生概率进行的估计，然后再根据后验概率进行调整。

6.1 共轭分布

如果先验分布 p(θ) 和似然函数 p(X|θ) 可以使得先验 p(θ) 和后验分布 p(θ|X) 有相同的形式，那么就称先验分布与似然函数是共轭分布.

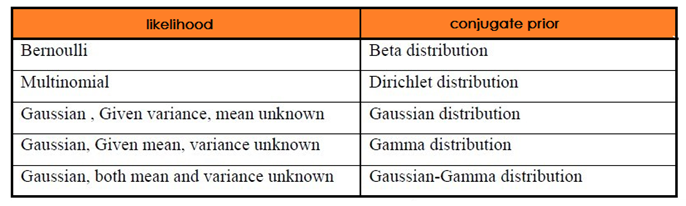
共轭性质：

• 当先验为 Beta ，似然为 Binomial分布时，后验仍然为 Beta ，但是这里的 Beta 是融入了 Binomial分布的计数的;
• 当先验为 Dirichlet，似然为 Multinomial 分布时，后验仍然为 Dirichlet，但是这里的 Dirichlet是融入了 Multinomial 分布的计数的.

6.2 Beta-Binomial distribution
假设，X|π∼Bin(n,π)，π∼Beta(α,β)
我们就可以根据数据得到π的先验概率，进而计算π的后验概率，最终推断出似然函数。

6.3 Dirichlet-MultiNomial distribution
略

二，Poisson 回归

我们回顾一下简介中提到的前两个问题，如果残差分布，以及变化函数是其他情况时，回归模型会变成什么情况？下面以poison回归为例进行思考。

• 当因变量研究的是计数或比率问题时：我们通常假设残差u服从Poisson分布（回归分析中假定x是确定性变量，由于残差服从泊松分布，所以因变量y也服从于泊松分布），

• G()变换为指数函数exp() (连接函数link=log())。则，此时对应的回归方程，则是Poisson回归。

1，假设我们有n个观测值，$y_1,y_2...,y_n$是分别服从泊松分布的随机变量，且$Y_i$ ~ $Poisson({\mu }_i)$

P r { Y = y } = e − μ μ y y ! Pr\{Y=y\}=\frac{e^{-μ}μ^y}{y!} Pr{Y=y}=y!e−μμy​

性质1：
且，满足(μ>0):
$E(Y)=var(Y)=\mu$

从上式可知，任何影响均值的因素都会影响到方差，所以，同方差性假设不再适用与泊松数据。

性质2：
如果，$Y_1$ ~ $P({\mu }_1)$，$Y_2$ ~ $P({\mu }_2)$，则 $Y_1+Y_2$ ~ $P({\mu }_1+{\mu }_2)$

2, log 变换

因为$E(y_i|x_i)={\mu }_i$，在线性概率模型中，我们研究的是 $E(y_i|x_i)$ 与 $x_i^{\prime }\beta$之间的线性关系，如果二者之间不再是线性关系，也不再像logistics中的logit关系，而是log关系，则

$log({\mu }_i)$=$x_i^{\prime }\beta$ 即为泊松回归模型的一般形式。

3，比率问题
单位时间或空间上的计数即为比率，对于泊松分布来说，问题转化为u/t
$log(\mu /t)=\alpha +\beta x$
$log(\mu )-log(t)=\alpha +\beta x$
$log(\mu )=\alpha +\beta x+log(t)$
$\mu =exp(\alpha +\beta x+log(t))=(t)exp(\alpha )exp(\beta x)$

三，GLM(广义线性模型)

我们回顾一下简介中提到的最后个问题，有没有什么通用的形式，能抽象的把一类变换的模型整理到一起呢？我们来做一些变换看看。

条件1，
我们定义线性自变量(linear predictor)
${\eta }_i={\beta }_0+{\beta }_1{x}_{1i}+...+{\beta }_p{x}_{pi}$

条件2，
我们定义连接方程(link function)，描述了因变量的期望与线性自变量之间的关系
$g({\mu }_i)={\eta }_i$

如果$\theta =\eta$，此时的连接方程又叫，Canonical link function.

例，对于线性回归方程来说，g(x)=x
所以，$g(\mu )=\mu =\eta$ ,即 $E(y)={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p$

条件3，因变量的方差，是其期望值方差的函数表达式

$Var(Y_i)=\frac{\varphi V({\mu }_i)}{w_i}$
其中，$\varphi$是方差的离散性参数，$w_i$是方差V(x)的权重，一般为1。
而，方差V(x)的函数表达式，因条件1的假设不同而不同。

满足前三个条件的前提下，
我们定义广义线性模型的一般形式为

f ( y ; θ , ϕ ) = e x p { y θ − b ( θ ) a ( ϕ ) + c ( y , ϕ ) } f(y;\theta,\phi)=exp\{\frac{y\theta-b(\theta)}{a(\phi)}+c(y,\phi) \} f(y;θ,ϕ)=exp{a(ϕ)yθ−b(θ)​+c(y,ϕ)}

其中，
$\mu =E(y;\theta ,\varphi )=b^{\prime }(\theta )$，$\mu$是一个关于$\theta$的函数
$var(y)=b^{\prime \prime }(\theta )a(\varphi )$

Y分布	$\theta$	Canonical link : g(x)	$\varphi$	$V(\mu )$	$E(y)=\mu (\theta )=b^{\prime }(\theta )$
Normal~$N(\mu ,{\sigma }^2)$	${\theta }_i={\eta }_i$	g(x)=x	${\sigma }^2$	1	$\theta$
Binomial~$B(m,\pi )/m$	${\theta }_i={\eta }_i$	g(x)=logit(x)=$log(\frac{x}{1-x})$	1/m	$\mu (1-\mu )$	$\frac{e^{\theta }}{(1+e^{\theta })}$
Poisson~$P(\mu )$	${\theta }_i={\eta }_i$	g(x)=ln(x)	1	$\mu$	$e^{\theta }$
Gamma~$G(\mu ,v)$	${\theta }_i={\eta }_i$	g(x)=1/x	$v^{-1}$	${\mu }^2$	$-\frac{1}{\theta }$
Inverse Gaussian~$IG(\mu ,{\sigma }^2/w)$	${\theta }_i={\eta }_i$	g(x)=$1/x^2$	${\sigma }^2$	${\mu }^3$	$(-2\theta {)}^{-1/2}$

根据Canonical link，${\theta }_i={\eta }_i$，即广义线性模型公式中的${\theta }_i$可以被替换为${\eta }_i$

并且又因
$\mu =E(y;\theta ,\varphi )=b^{\prime }(\theta )$
$\eta =g(\mu )$
$\mu =g^{-1}(\eta )=b^{\prime }(\theta )=b^{\prime }(\eta )$
$g^{-1}(\eta )=b^{\prime }(\eta )$
所以，$g^{-1}()=b^{\prime }()$

上一节：第3章-从线性概率模型到广义线性模型(1)

---

原文参考
斯坦福机器学习cs229-2-Generative Learning algorithms
https://mathdept.iut.ac.ir/sites/mathdept.iut.ac.ir/files/AGRESTI.PDF
http://data.princeton.edu/wws509/notes/c4a.pdf
http://www.cnblogs.com/ooon/p/5845917.html
https://www.casact.org/pubs/dpp/dpp04/04dpp1.pdf

这篇关于第3章-从线性概率模型到广义线性模型(2)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---